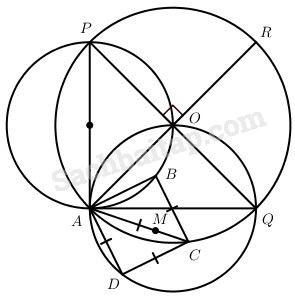
Câu 74 trang 17 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 74 trang 17 Sách bài tập Hình học 11 Nâng cao Cho điểm A cố định nằm trên đường tròn (O) và điểm C thay đổi trên đường tròn đó. Dựng hình vuông ABCD. Tìm quỹ tích điểm B và điểm D. Trả lời: Trên đoạn thẳng AC lấy điểm M sao cho AM = AB = AD. Khi đó, ta có \({{AM} \over {AC}} = {{AB} \over {AC}} = {{\sqrt 2 } \over 2}.\) Ngoài ra \(\left( {AM,AB} \right) = {45^0}\) và \(\left( {AM,A{\rm{D}}} \right) = - {45^0}\) . Suy ra, phép vị tự V tâm A tỉ sơ \(k = {{\sqrt 2 } \over 2}\) biến điểm C thành điểm M và phép quay Q tâm A góc 450 biến điểm M thành điểm B. Vậy nếu gọi F là phép hợp thành của V và Q thì F biến C thành B. Vì quỹ tích của C là đường tròn (O), nên quỹ tích của B là ảnh của đường tròn đó qua phép đồng dạnh. Đường tròn quỹ tích B có thể xác định như sau: Gọi AR là đường kính của (O) và PQ là đường kính của (O) vuông góc với AR (ta kí hiệu các điểm P, Q sao cho (AR, QP = 450). Khi đó dễ thấy rằng phép đồng dạng F biến AR thành AP. Vậy quỹ tích B là đường tròn đường kính AP. Tương tự ta được quỹ tích D là đường tròn đường kính AQ. Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương I - Phép dời hình và phép đồng dạng
|

 Tải ngay
Tải ngay