Tải ngay
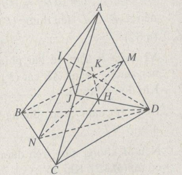
Câu 8 trang 51 Sách bài tập Hình học 11 nâng cao.Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. 8. Trang 51 sách bài tập Hình học 11 nâng cao. Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. a) Xác định giao tuyến của hai mặt phẳng (MBC) và (NDA). b) Cho I, J là hai điểm lần lượt nằm trên hai đoạn thẳng AB và AC. Xác định giao tuyến của hai mặt phẳng (MBC) và (IJD). Giải
a) Ta có \(\left( {MBC} \right) \cap \left( {NAD} \right) = MN\). b) Gọi K là giao điểm của MB với ID và H là giao điểm của MC với DJ thì rõ ràng K và H là hai điểm chung của hai mặt phẳng (MBC) và (IJD) nên: \(\left( {MBC} \right) \cap \left( {IJD} \right) = KH\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 1: Đại cương về đường thẳng và mặt phẳng
|
-
Câu 10 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K theo thứ tự là hai điểm trong của các tam giác ABC và BCD. Giả sử đường thẳng IK cắt mặt phẳng (ACD) tại J. Hãy xác định giao điểm J đó.
-
Câu 11 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm không đồng phẳng A, B, C, D; G là trọng tâm của tam giác ACD.
-
Câu 12 trang 52 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD. Trên cạnh SC lấy một điểm E không trùng với hai điểm S và C.
