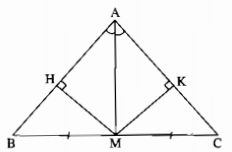
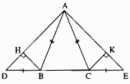
Câu 98 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1Chứng minh rằng tam giác ABC là tam giác cân. Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Chứng minh rằng tam giác ABC là tam giác cân. Giải
Kẻ \(MH \bot AB,MK \bot AC\) Xét hai tam giác vuông AHM và AKM, ta có: \(\eqalign{ AM cạnh huyền chung \( \Rightarrow \) ∆AHM = ∆AKM (cạnh huyền, góc nhọn) Suy ra: MH = MK (hai cạnh tương ứng) Xét hai tam giác vuông MHB và MKC, ta có: \(\widehat {MHB} = \widehat {MKC} = 90^\circ \) MH = MK (chứng minh trên) MB = MC (gt) Suy ra: ∆MHB = ∆MKC (cạnh huyền, cạnh góc vuông) Suy ra: \(\widehat B = \widehat C\) (hai góc tương ứng) Vậy ∆ABC cân tại A. Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 8: Các trường hợp bằng nhau của tam giác vuông
|
-
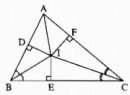
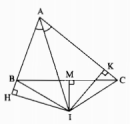
Câu 100 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Chứng minh rằng AI là tia phân giác của góc A.
-
Câu 102 trang 152 Sách Bài Tập (SBT) Toán lớp 7 tập 1
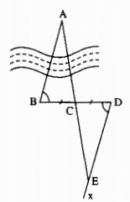
Dựa vào hình 68 hãy nêu cách xác định khoảng cách giữa hai điểm A, B bị ngăn bởi con sông.

 Tải ngay
Tải ngay