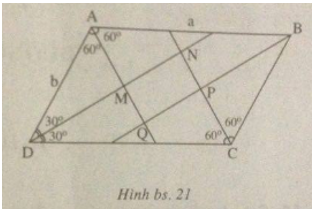
Câu I.4 trang 123 Sách Bài Tập (SBT) Toán 9 Tập 1Cho hình bình hành ABCD có Cho hình bình hành ABCD có \(\widehat A = 120^\circ \), AB = a, BC = b. Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ. Gợi ý làm bài (h.bs.21).
Đường phân giác của góc A cắt đường phân giác của góc D tại M thì tam giác ADM có hai góc bằng 60º và 30º nên các đường phân giác đó vuông góc với nhau. Lập luận đó chứng tỏ hình MNPQ có 4 góc vuông nên MNPQ là hình chữ nhật. Trong tam giác vuông ADM có \(DM = AD\sin \widehat {DAM} = b\sin 60^\circ = {{b\sqrt 3 } \over 2}.\) Trong tam giác vuông DCN ( N là giao của đường phân giác góc D và đường phân giác góc C) có \(DN = DC\sin \widehat {DCN}{\rm{ = asin60}}^\circ {\rm{ = }}{{a\sqrt 3 } \over 2}.\) Vậy \(MN = DN - DM = (a - b){{\sqrt 3 } \over 2}.\) Trong tam giác vuông DCN có \(CN = CD\cos 60^\circ = {a \over 2}.\) Trong tam giác vuông BCP ( P là giao của đường phân giác góc C với đường phân giác góc B) có \(CP = CB\cos 60^\circ = {b \over 2}.\) Vậy: \(NP = CN - CP = {{a - b} \over 2}.\) Suy ra diện tích hình chữ nhật MNPQ là \(MN \times NP = {(a - b)^2}{{\sqrt 3 } \over 4}\) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương I - Hệ thức lượng trong tam giác vuông
|
-
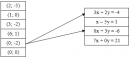
Câu 1 trang 5 Sách bài tập (SBT) Toán 9 tập 2
Hãy dùng mũi tên (như trong hình vẽ) chỉ rõ mỗi cặp số là nghiệm của phương trình nào.
-

Câu 2 trang 5 Sách bài tập (SBT) Toán 9 tập 2
Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình.

 Tải ngay
Tải ngay