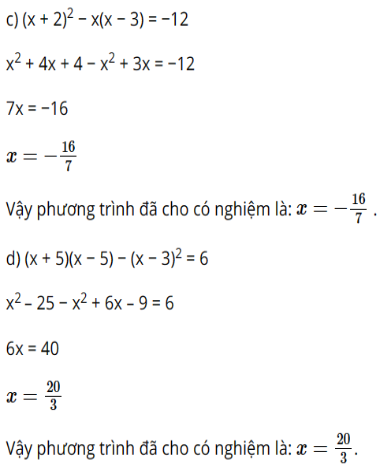Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 trang 41, 42 SGK Toán 8 Chân trời sáng tạo tập 2Giải SGK Toán lớp 8 trang 41, 42 Chân trời sáng tạo tập 2. Một tổ may có kế hoạch mỗi ngày phải may 30 chiếc áo. Trong thực tế mỗi ngày tổ đã may được 40 chiếc áo. Do đó xưởng đã hoàn thành kế hoạch sớm hơn 3 ngày và may thêm được 20 chiếc áo nữa. Tính số áo mà tổ may theo kế hoạch. Câu hỏi trắc nghiệm. Bài 1 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Phương trình \(ax + b = 0\) là phương trình bậc nhất một ẩn nếu A. \(a = 0\). B. \(b \ne 0\). C. \(b = 0\). D. \(a \ne 0\). Phương pháp: Phương trình bậc nhất có dạng \(ax + b = 0\) với \(a\) và \(b\a) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số. Lời giải: Đáp án đúng là: D Để phương trình ax + b = 0 là phương trình bậc nhất một ẩn thì a ≠ 0. Bài 2 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Phương trình nào dưới đây là phương trình bậc nhất một ẩn? A. \(3x + 2y - 6 = 0\). B. \(3x + 6 = 0\). C. \({x^2} = 4\). D. \({y^2} - x + 1 = 0\). Phương pháp: Phương trình bậc nhất có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số. Lời giải: Đáp án đúng là: B Phương trình bậc nhất một ẩn là 3x + 6 = 0. Bài 3 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Phương trình nào sau đây nghận \(x = 2\) là nghiệm? A. \(3x + 6 = 0\). B. \(2x - 4 = 0\). C. \(2x + 3 = 1 + x\). D. \(x + 2 = 4 + x\). Phương pháp: Để giải phương trình ta có thể sử dụng các quy tắc sau: - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Lời giải: Đáp án đúng là: B Thay x = 2 vào 2x – 4 = 0 ta có: 2.2 – 4 = 0. Suy ra 2x – 4 = 0 nhận x = 2 là nghiệm. Bài 4 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Nghiệm của phương trình \(5x + 3 = 18\) là A. \(x = - 3\). B. \(x = 5\). C. \(x = 3\). D. \(x = - 5\). Phương pháp: Để giải phương trình ta có thể sử dụng các quy tắc sau: - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Lời giải: Đáp án đúng là: C Ta có: 5x + 3 = 18 5x = 18 – 3 = 15 x = 15 : 5 x = 3 Vậy phương trình đã cho có nghiệm là x = 3. Bài 5 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Phương trình \(x - 4 = 10 - x\) có nghiệm là A. \(3\). B. \(14\). C. \(7\). D. \( - 7\). Phương pháp: Để giải phương trình ta có thể sử dụng các quy tắc sau: - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Lời giải: Đáp án đúng là: C Ta có: x – 4 = 10 – x 2x = 14 x = 7 Vậy phương trình đã cho có nghiệm là x = 7. Bài 6 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Cho biết \(3x - 9 = 0\). Khi đó giá trị của biểu thức \({x^2} - 2x - 3\) là A. \( - 3\). B \(1\). C. \(0\). D. \(6\). Phương pháp: Để giải phương trình ta có thể sử dụng các quy tắc sau: - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Giá trị của biểu thức \(f\left( x \right)\) khi \(x = a\) là \(f\left( a \right)\). Lời giải: Đáp án đúng là: C Ta có: 3x – 9 = 0 suy ra x = 3 Thay x = 3 vào biểu thức x2 − 2x − 3 ta có: 32 − 2.3 – 3 = 0. Bài tập tự luận. Bài 7 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Giải các phương trình sau: a) \(5x - 12 = 3\); b) \(2,5y + 6 = - 6,5\); c) \(\dfrac{1}{5}x - 2 = \dfrac{3}{5}\); d) \(\dfrac{1}{2}x + \dfrac{2}{3} = x + 1\). Phương pháp: Để giải phương trình ta có thể sử dụng các quy tắc sau: - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Lời giải: a) 5x – 12 = 3 5x = 3 + 12 5x = 15 x = 15 : 5 x = 3 Vậy phương trình đã cho có nghiệm là x = 3. b) 2,5y + 6 = –6,5 2,5y = –6,5 – 6 2,5y = –12,5 y = –5 Vậy phương trình đã cho có nghiệm là y = −5.
Bài 8 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Giải các phương trình sau: a) \(10 - \left( {x - 5} \right) = 20\); b) \( - 12 + 3\left( {1,5 - 3u} \right) = 15\); c) \({\left( {x + 2} \right)^2} - x\left( {x - 3} \right) = - 12\); d) \(\left( {x + 5} \right)\left( {x - 5} \right) - {\left( {x - 3} \right)^2} = 6\). Phương pháp: Để giải phương trình ta có thể sử dụng các quy tắc sau: - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). - Khi bỏ dấu ngoặc mà đằng trước dấu ngoặc có dấu cộng, ta bỏ ngoặc và giữ nguyên dấu của các số hạng trong ngoặc. Khi bỏ dấu ngoặc mà đằng trước dấu ngoặc có dấu trừ, ta bỏ ngoặc và đổi dấu các số hạng trong ngoặc (Quy tắc dấu ngoặc). Lời giải: a) 10 − (x − 5) = 20 10 − x + 5 = 20 x = 10 + 5 − 20 x = −5 Vậy phương trình đã cho có nghiệm là x = −5. b) −12 + 3(1,5 − 3u) = 15 −12 + 4,5 − 9u = 15 9u = −12 + 4,5 − 15 9u = −22,5 u = −2,5 Vậy phương trình đã cho có nghiệm là u = −2,5.
Bài 9 trang 41 SGK Toán 8 tập 2 - Chân trời sáng tạo Giải các phương trình sau: a) \(\frac{{3x - 1}}{6} = \frac{{3 + 2x}}{3}\); b) \(\frac{{x + 5}}{3} = 1 - \frac{{x - 2}}{4}\); c) \(\frac{{3x - 2}}{5} + \frac{3}{2} = \frac{{4 - x}}{{10}}\); d) \(\frac{x}{3} + \frac{{2x + 1}}{6} = \frac{{4\left( {x - 2} \right)}}{5}\) Phương pháp: - Quy đồng mẫu số. - Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Lời giải:
Bài 10 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Một tổ may có kế hoạch mỗi ngày phải may 30 chiếc áo. Trong thực tế mỗi ngày tổ đã may được 40 chiếc áo. Do đó xưởng đã hoàn thành kế hoạch sớm hơn 3 ngày và may thêm được 20 chiếc áo nữa. Tính số áo mà tổ may theo kế hoạch. Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải: Gọi số áo tổ phải sản xuất theo kế hoạch là x áo (x ∈ ℕ, x > 0) Vậy số áo cần làm theo kế hoạch là 30x (áo) Số áo làm trong thời gian ít hơn kế hoạch 3 ngày với năng suất dự thực tế là: 40(x − 3) (áo) Vì tổ đó làm thêm được 20 cái áo nữa so với kế hoạch nên ta có phương trình: 40(x − 3) − 20 = 30x 40x − 120 − 20 = 30x 10x = 140 x = 14 (thỏa mãn điều kiện) Thời gian hoàn thành công việc là 14 ngày. Số áo cần may là: 14.30 = 420 (áo). Vậy số áo mà tổ đó phải may theo kế hoạch là 420 áo. Bài 11 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Trong một cuộc thi, học sinh cần trả lời 50 câu hỏi trắc nghiệm, mỗi câu trả lời đúng được 5 điểm, mỗi câu trả lời sai (hoặc không trả lời) bị trừ 2 điểm. An đã tham gia cuộc thi trên và đã ghi đường tổng cộng là 194 điểm. Hỏi An trả lời đúng mấy câu? Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải: Gọi x (câu) là số câu trả lời đúng (x ∈ ℕ*). Khi đó, số câu sai là: 50 – x (câu) Do đó ta có phương trình: 5x – 2(50 – x) = 194 5x –100 + 2x = 194 7x = 194 + 100 7x = 294 x = 294 : 7 x = 42 (TMĐK) Vậy An trả lời đúng 42 câu. Bài 12 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Biết rằng trong 500 g dung dịch nước muối chứ 150 g muối nguyên chất. Hỏi cần phải thêm vào dung dịch đó bao nhiêu gam nước để dung dịch đó có nồng độ là \(20\% \)? Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Chú ý: Trong dung dịch, nồng độ phần trăm được tính theo công thức: \(C\% = \frac{{{m_{ct}}}}{{{m_{dd}}}}\) trong đó, \({m_{ct}}\) là khối lượng chất tan và \({m_{dd}}\) là khối lượng dung dịch. Lời giải: Gọi khối lượng nước cần thếm là a (g) (a > 0) Tổng khối lượng dung dịch mới là 500 + x (g) Lượng muối trong dung dịch mới là: 0,2(500 + x) Vì lượng muối không thay đổi nên ta có phương trình: 0,2(500 + x) = 150 100 + 0,2x = 150 0,2x = 150 – 100 x = 250 Vậy lượng nước cần thêm vào dung dịch là 250 g. Bài 13 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Một ô tô dự định đi từ A đến B với tốc độ 50 \(km/h\). Sau khi đi được \(\frac{2}{3}\) quãng đường với vận tốc đó, vì đường xấu nên người lái xe phải giảm tốc độ còn 40 \(km/h\) trên quãng đường còn lại. Vì thế ô tô đã đến B chậm hơn dự định 30 phút. Tính chiều dài quãng đường AB. Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Chú ý: Ta có công thức biểu diễn quãng đường, vận tốc, thời gian như sau: \(s = vt\) với \(s\) là quãng đường; \(v\) là vận tốc; \(t\) là thời gian. Lời giải:
Bài 14 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu tăng chiều dài thêm 3 \(m\) và giảm chiều rộng 2 \(m\) thì diện tích giảm 90 \({m^2}\). Tính chiều dài và chiều rộng của hình chữ nhật. Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Chú ý: Diện tích hình chữ nhật bằng tích của chiều dài và chiều rộng. Lời giải: Gọi chiều rộng của hình chữ nhật là: x (m) (x > 0) Chiều dài của hình chữ nhật là: 3x (m) Diện tích ban đầu của hình chữ nhật là: 3x2 (m2) Nếu tăng chiều dài thêm 2m và giảm chiều rộng 3m thì diện tích mới của hình chữ nhật là: (x – 3)(3x + 2) (m2) Do diện tích mới giảm 90 m2 nên ta có phương trình: 3x2 − (x − 3)(3x + 2) = 90 3x2 − 3x2 − 2x + 9x + 6 = 90 7x = 84 x = 12 (TMĐK) Vậy: Chiều rộng ban đầu của hình chữ nhật là: 12 m. Chiều dài ban đầu của hình chữ nhật là: 12.3 = 36 (m). Bài 15 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Trong tháng 4, một công nhân nhận được tiền lương là 7 800 000 đồng gồm tiền lương của 24 ngày làm việc bình thường và 4 ngày làm tăng ca (ngày Chủ nhật và ngày lễ). Biết tiền lương của một ngày tăng ca nhiều hơn tiền lương của một ngày làm việc bình thường là 200 000 đồng. Tính tiền lương của một ngày làm việc bình thường. Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải: Gọi tiền lương của một ngày bình thường là x (đồng) (x > 0) Số tiền người đó nhận được khi làm 24 ngày bình thường là: 24x (đồng) Tiền lương của một ngày đặc biệt là : x + 200 000 (đồng) Số tiền người đó nhận được khi làm 4 ngày đặc biệt là: 4(x + 200 000) = 4x + 800 000 (đồng) Vì tháng đó người đó nhận được tiền lương là 7 800 000 đồng nên ta có phương trình: 24x + 4x + 800 000 = 780 0000 24x + 4x = 780 0000 – 800 000 28x = 700 0000 x = 250 000 (thỏa mãn) Vậy tiền lương của một ngày bình thường là 250 000 đồng. Bài 16 trang 42 SGK Toán 8 tập 2 - Chân trời sáng tạo Một siêu thị diện máy có chương trình khuyến mãi giảm giá tủ lạnh, sau hai lần giảm giá, mỗi lần giảm \(20\% \) so với giá tại thời điểm đó thì giá bán của một chiếc tủ lạnh là 12 800 000 đồng. Tính giá tiền tủ lạnh đó lúc chưa giảm giá lần nào. Phương pháp: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải: Gọi giá ban đầu của tủ lạnh là a (đồng) (a > 12 800 000) Giá tủ lạnh sau lần giảm thứ nhất: 0,8a (đồng) Giá tủ lạnh sau lần giảm thứ hai: 0,82a (đồng) Theo đề bài ta có phương trình: 0,82a = 12 800 000 a = 20 000 000 (TMĐK) Vậy giá ban đầu của tủ lạnh là 20 000 000 đồng. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 6
|

 Tải ngay
Tải ngay