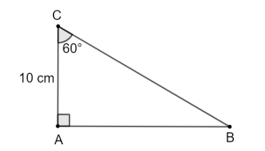
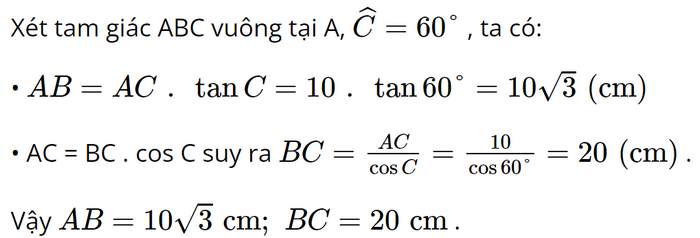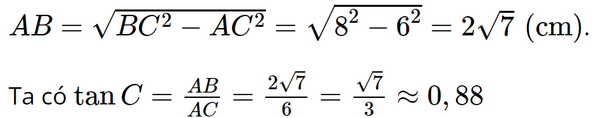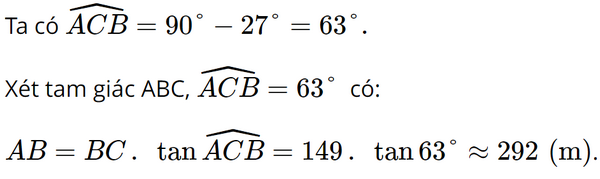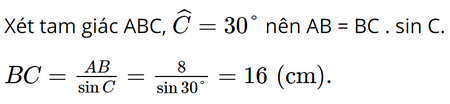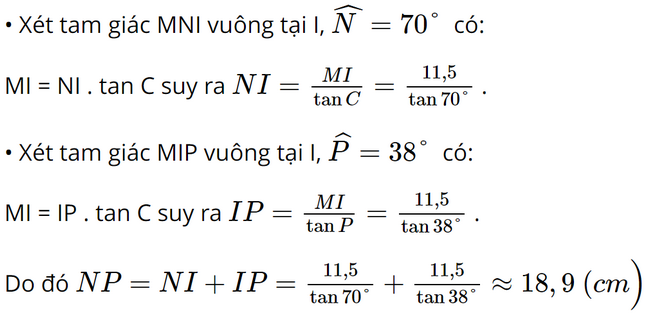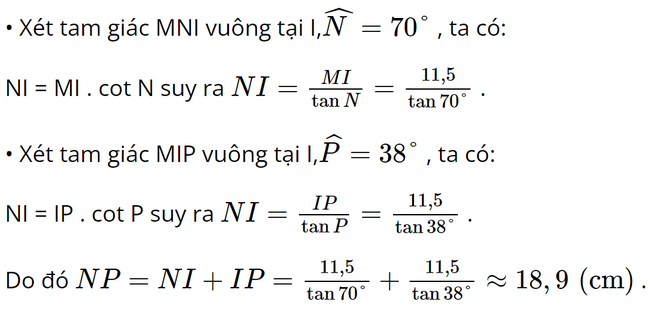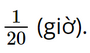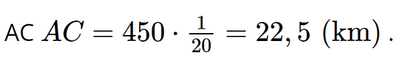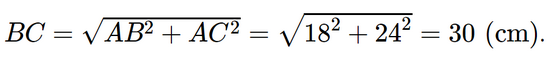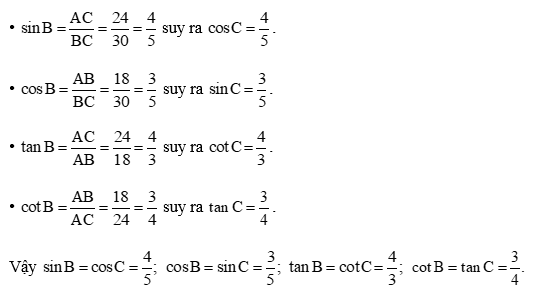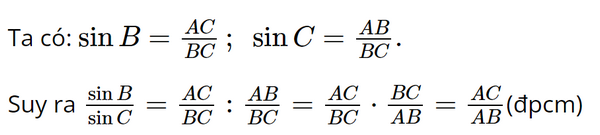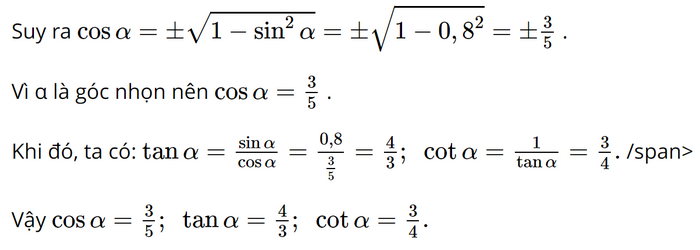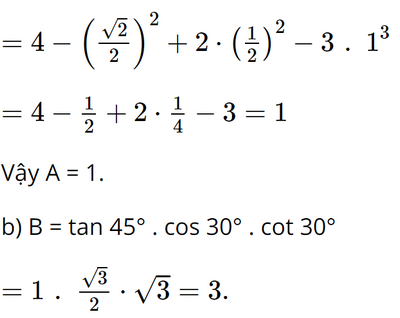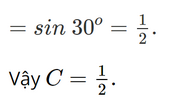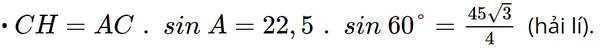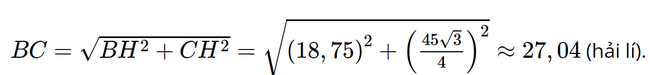Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 trang 72 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A có AC = 10 cm, \(\widehat C = {60^o}\). Độ dài hai cạnh còn lại là:

A. \(AB = \frac{{5\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)

B. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{14\sqrt 3 }}{3}cm\)

C. \(AB = 10\sqrt 3 cm;BC = 20cm\)

D. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)

Phương pháp:

Đọc kĩ dữ liệu đề bài để vẽ hình

Dựa vào định lí: Xét tam giác vuông :

+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.

+ Áp dụng định lý Pythagore trong tam giác vuông tìm cạnh góc vuông còn lại.

Lời giải:

Đáp án đúng là: C

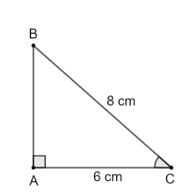
Bài 2 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A có BC = 8 cm, AC = 6 cm. Tỉ số lượng giác tan C (kết quả làm tròn đến hàng phần trăm) là

A. 0,87

B. 0,86

C. 0,88

D. 0,89

Phương pháp:

-  Đọc kĩ dữ liệu đề bài để vẽ hình

-  Áp dụng định lý pythagore tính cạnh góc vuông còn lại

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông ta có tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.

Lời giải:

Đáp án đúng là: C

Áp dụng định lí Pythagore vào tam giác ABC, ta có:

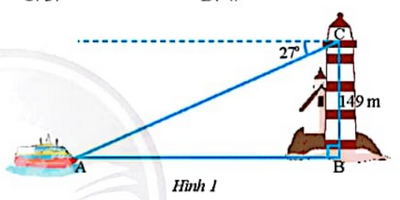
Bài 3 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Giá trị của biểu thức \(B = tan{20^o}.\tan {30^o}.\tan {40^o}.\tan {50^o}.\tan {60^o}.tan{70^o}\) là

A. 2

B. 1

C. 3

D. 4

Phương pháp:

Sử dụng kiến thức: \(\cot ({90^0} - \alpha ) = \tan \alpha \); \(\tan \alpha .\cot \alpha  = 1\).

Lời giải:

Đáp án đúng là: B

B = tan 20° . tan 30° . tan 40° . tan 50° . tan 60° . tan 70°

= tan 20° . tan 30° . tan 40° . cot (90° − 50°) . cot (90° − 60°) . cot (90° − 70°)

= tan 20° . tan 30° . tan 40° . cot 40° . cot 30° . cot 20°

= (tan 20° . cot 20°) . (tan 30° . cot 30°) . (tan 40° . cot 40°)

= 1 . 1 . 1 = 1.

Vậy giá trị biểu thức B là 1.

Bài 4 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Một người quan sát tại ngọn hải đăng ở vị trí cao 149 m so với mặt nước biển thì thấy một du thuyền ở xa với góc nghiêng xuống là 27^o (Hình 1). Hỏi thuyền cách xa chân hải đăng bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

A. 292 m

B. 288 m

C. 312 m

D. 151 m 

Phương pháp:

Tính góc ACB. Sau đó áp dụng Định lí: Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề.

Lời giải:

Đáp án đúng là: A

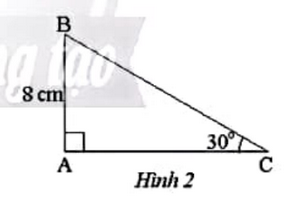
Vậy thuyền cách xa chân hải đăng khoảng 292 mét.

Bài 5 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho Hình 2.

Độ dài cạnh BC là:

A. 4 cm

B. \(8\sqrt 3 \) cm

C. \(\frac{{8\sqrt 3 }}{3}\) cm

D. 16 cm 

Phương pháp:

Tính góc ACB.

Sau đó áp dụng Định lí: Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề.

Lời giải:

Đáp án đúng là: D

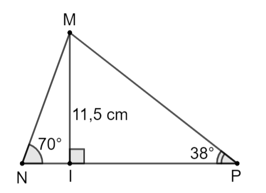
Vậy BC = 16 cm.

Bài 6 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác MNP có \(\widehat N = {70^o},\widehat P = {38^o}\), đường cao MI = 11,5 cm. Độ dài cạnh NP của tam giác MNP (kết quả làm tròn đến hàng phần mười) bằng

A. 20,9 cm

B. 18,9 cm

C. 40,6 cm

D. 16,9 cm 

Phương pháp:

-  Đọc kĩ dữ liệu đề bài để vẽ hình

-  Áp dụng Định lí: Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề để tính cạnh góc vuông NI và IP.Suy ra cạnh NP.

Lời giải:

Đáp án đúng là: B

Vậy độ dài của cạnh NP của tam giác MNP là 18,9 cm.

Bài 7 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Một cái thang dài 3m đặt sát bờ tường, biết góc tạo bởi thang và bờ tường là 40^o . Hỏi chân thang đặt ở vị trí cách tường bao nhiêu mét (kết quả làm tròn đến hàng phần mười)?

A. 1,9 m

B. 2,3 m

C. 1,8 m

D. 2,5 m 

Phương pháp:

Đọc kĩ dữ liệu đề bài để vẽ hình

Áp dụng Định lí: Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề để tính cạnh góc vuông.

Lời giải:

Đáp án đúng là: B

Vậy độ dài của cạnh NP của tam giác MNP khoảng 18,9 cm.

Bài 8 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Một chiếc máy bay bay lên với tốc độ 450 km/h. Đường bay len tạo với phương nằm ngang một góc 30^o . Hỏi sau 3 phút kể từ lúc cất cánh, máy bay cách mặt đất bao nhiêu kilomet theo phương thẳng đứng?

A. 10,5 km

B. 12,75 km

C. 12 km

D. 11,25 km 

Phương pháp:

Đọc kĩ dữ liệu đề bài để vẽ hình

Áp dụng công thức S = v.t để tính quãng đường máy bay bay được. Sau đó áp dụng định lí: Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề để tính máy bay cách mặt đất bao nhiêu km.

Lời giải:

Theo đề bài, ta có hình vẽ:

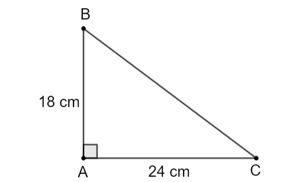
Đổi 3 phút $=$

Xét tam giác ABC vuông tại B.

Quãng đường máy bay bay được là:

Suy ra độ cao máy bay bay được sau 3 phút so với mặt đất chính là BC, ta có

BC = AC . sin 30° = 22,5 . sin 30° = 11,25 (km).

Vậy sau 3 phút kể từ lúc cất cánh, máy bay cách mặt đất 11,25 kilômét theo phương thẳng đứng.

Bài 9 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tìm số đo góc \(\alpha \), biết rằng:

a) sin\(\alpha \) = 0,25

b) sin\(\alpha \) = 0,75

c) tan\(\alpha \) = 1

d) cot\(\alpha \) = 2.

Phương pháp:

Sử dụng máy tính cầm tay để tìm góc \(\alpha \).

Lời giải:

a) sin α = 0,25 nên α ≈ 14,5°.

b) cos α = 0,75 nên α ≈ 41,4°.

c) tan α = 1 nên α = 45°.

d) cot α = 2 nên α ≈ 0,02°.

Bài 10 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A có AB = 18 cm, AC = 24 cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.

Phương pháp:

-  Đọc kĩ dữ liệu đề bài để vẽ hình

-  Áp dụng định lý Pythagore trong tam giác vuông để tính cạnh huyền

-  Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin, kí hiệu cos.

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang , kí hiệu cot.

-  Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.

Lời giải:

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

Các tỉ số lượng giác của góc B là:

Bài 11 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A. Chứng minh rằng \(\frac{{AC}}{{AB}} = \frac{{\sin B}}{{\sin C}}\).

Phương pháp:

-  Đọc kĩ dữ liệu đề bài để vẽ hình

-  Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông, tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.

-  Suy ra tỉ số cần tìm.

Lời giải:

Bài 12 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho góc nhọn \(\alpha \) biết sin\(\alpha \) = 0,8. Tính cos\(\alpha \), tan \(\alpha \) và cot\(\alpha \).

Phương pháp:

Dựa vào công thức:

\(\begin{array}{l}{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\\\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\\\cot \alpha  = \frac{1}{{\tan \alpha }}\end{array}\)

Lời giải:

Ta có sin² α + cos² α = 1.

Bài 13 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính giá trị biểu thức:

a) A = \(4 - {\sin ^2}{45^o} + 2{\cos ^2}{60^o} - 3{\cot ^3}{45^o}\)

b) B = \(\tan {45^o}.\cos {30^o}.\cot {30^o}\)

c) C = \(\sin {15^o} + \sin {75^o} - cos{15^o} - co{\mathop{\rm s}\nolimits} {75^o} + \sin {30^o}\)

Phương pháp:

-  Dựa vào VD2 trang 62 làm tương tự

-  Áp dụng nếu hai góc phụ nhau thì sin góc này bằng cos góc kia.

Lời giải:

a) A = 4 – sin² 45° + 2cos² 60° – 3cot³ 45°

= 4 – sin²45^o + 2cos²60^o – 3cot³45^o

Vậy B = 3.

c) C = sin 15° + sin 75° – cos 15° – cos 75° + sin 30°.

= (sin 15^o – cos 75^o) + (sin 75^o – cos 15^o) + sin 30^o

= (sin 15^o – sin 15^o) + (cos 15^o – cos 15^o) + sin 30^o

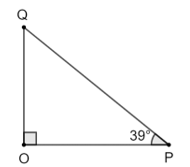
Bài 14 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác OPQ vuông tại O có \(\widehat P = {39^o}\) và PQ = 10 cm. Hãy giải tam giác vuông OPQ.

Phương pháp:

-  Đọc kĩ dữ liệu đề bài để vẽ hình

-  Áp dụng tổng 2 góc phụ nhau bằng 90^o để tìm góc Q

-  Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.

Lời giải:

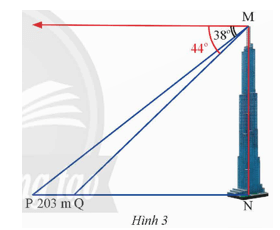
Bài 15 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hai điểm P và Q cách nhau 203 m và thẳng hàng với chân một tòa tháp (Hình 3). Từ đỉnh của tòa tháp đó, một người nhìn thấy hai điểm P, Q với hai góc nghiêng xuống lần lượt là \({38^o}\) và \({44^o}\). Tính chiều cao của tòa tháp (kết quả làm tròn đến hàng đơn vị của mét).

Phương pháp:

-  Tìm \(\widehat {QMN}\) và \(\widehat {PMN}\)

-  Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông.

-  Từ đó lập biểu thức PN – QN = 203 để tính MN.

Lời giải:

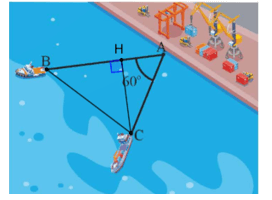
Bài 16 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hai điểm tàu thủy B và C cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo thành một góc 60^o (Hình 4). Tàu B chạy với tốc độ 20 hải lí/giờ, tàu C chạy với tốc độ 15 hải lý/giờ. Hỏi sau 1,5 giờ hai tàu B và C cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?

Phương pháp:

-  Áp dụng công thức S = v.t để tính quãng đường tàu B và C đi được sau 1,5 giờ

-  Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.

-  Áp dụng định lý Pythagore lần lượt vào 2 tam giác vuông ACH và CHB để tìm ra BC.

Lời giải:

Nối B và C. Kẻ CH ⊥ AB (H ∈ AB).

Sau 1,5 giờ tàu B chạy được quãng đường là:

AB = 20.1,5 = 30 (hải lí).

Sau 1,5 giờ tàu C chạy được quãng đường là:

AC = 15.1,5 = 22,5 (hải lí).

Xét tam giác AHC vuông tại H, ta có:

• AH = AC . cos A = 22,5 . cos 60° = 11,25 (hải lí).

Do đó BH = AB – AH = 30 – 11,25 = 18,75 (hải lí).

Mặt khác, tam giác CHB vuông tại H, áp dụng định lý Pythagore ta có:

Vậy sau 1,5 giờ tàu B cách tàu C là 27,04 hải lí.

Sachbaitap.com