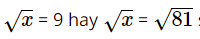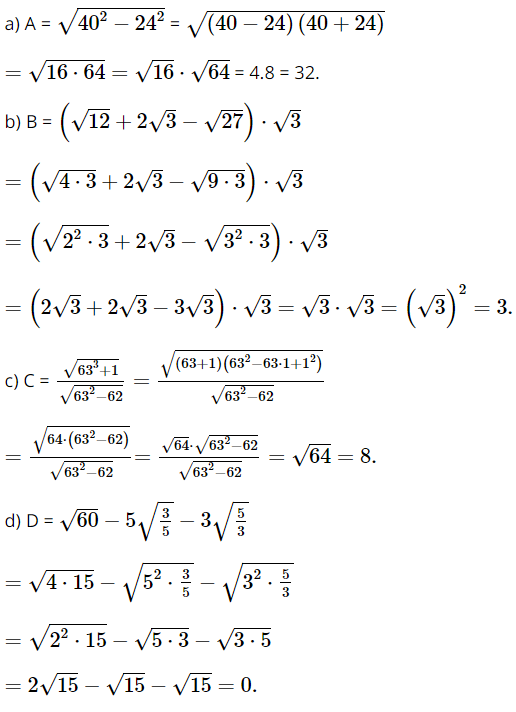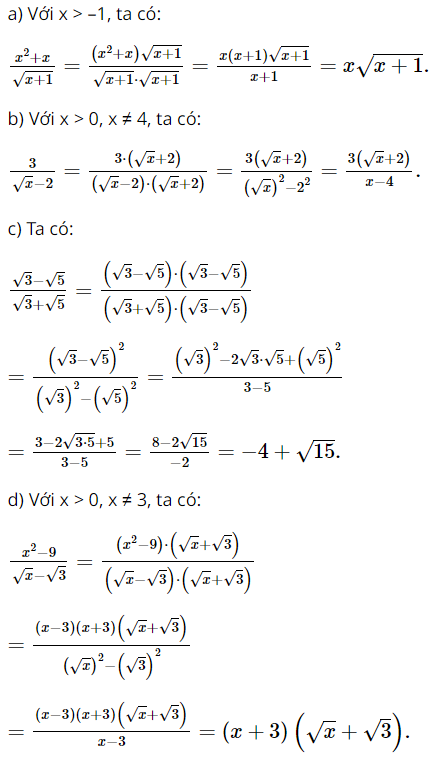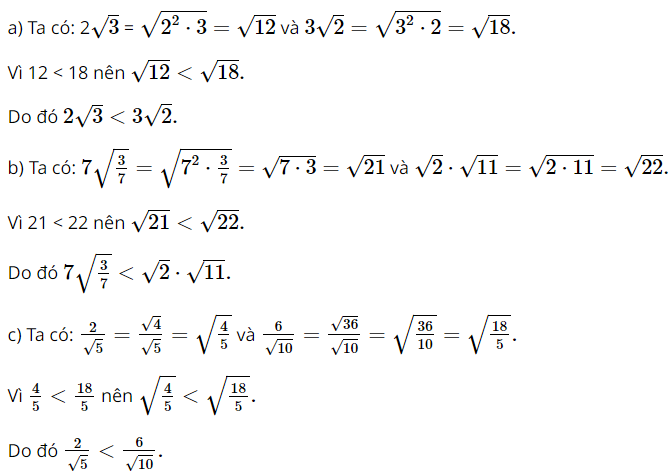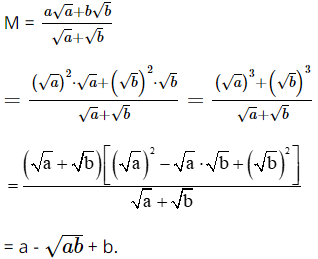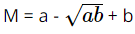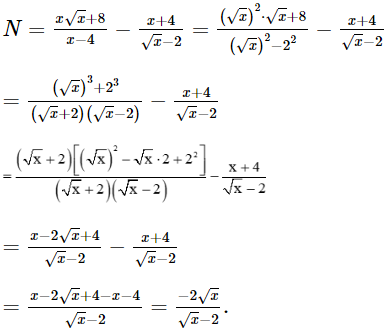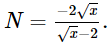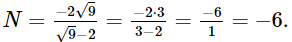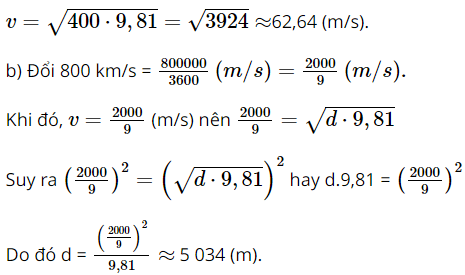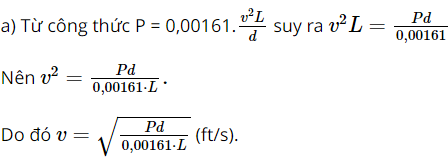Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 72, 73 SGK Toán 9 Cánh Diều tập 1Khi bay vào không gian, trọng lượng P(N) của một phi hành gia ở vị trí cách mặt đất một độ cao h(m) được tính theo công thức: (P = frac{{28014.10_{}^{12}}}{{left( {64.10_{}^5 + h} right)_{}^2}}).a. Trọng lượng của phi hành gia là bao nhiêu Newton khi cách mặt đất 10 000 m (làm tròn kết quả đến hàng phần mười)? b. Ở độ cao bao nhiêu mét thì trọng lượng của phi hành gia là 619N (làm tròn kết quả đến hàng phần mười)? Bài 1 trang 72 SGK Toán 9 tập 1 - Cánh Diều Căn bậc hai của 16 là: A. 4. B. 4 và – 4. C. 256. D. 256 và – 256. Phương pháp: Dựa vào kiến thức “Căn bậc hai của một số thực a không âm là số thực x sao cho \(x_{}^2 = a\)” để giải bài toán. Lời giải: Đáp án đúng là: B Ta có nên Bài 2 trang 72 SGK Toán 9 tập 1 - Cánh Diều Nếu \(\sqrt x = 9\) thì \(x\) bằng: A. 3. B. 3 hoặc – 3. C. 81. D. 81 hoặc – 81. Phương pháp: Dựa vào kiến thức “Căn bậc hai của một số thực a không âm là số thực x sao cho \(x_{}^2 = a\)” để giải bài toán. Lời giải: Đáp án đúng là: C Ta có: Bài 3 trang 72 SGK Toán 9 tập 1 - Cánh Diều Rút gọn biểu thức: a. \(A = \sqrt {40_{}^2 - 24_{}^2} \); b. \(B = \left( {\sqrt {12} + 2\sqrt 3 - \sqrt {27} } \right).\sqrt 3 \); c. \(C = \frac{{\sqrt {63_{}^3 + 1} }}{{\sqrt {63_{}^2 - 62} }}\); d. \(D = \sqrt {60} - 5\sqrt {\frac{3}{5}} - 3\sqrt {\frac{5}{3}} \). Phương pháp: Áp dụng các kiến thức về căn bậc hai của một thương, căn bâc hai của một tích, đưa thừa số vào trong căn bậc hai và đưa thừa số ra ngoài căn bậc hai để giải bài toán. Lời giải:
Bài 4 trang 72 SGK Toán 9 tập 1 - Cánh Diều Trục căn thức ở mẫu: a. \(\frac{{x_{}^2 + x}}{{\sqrt {x + 1} }}\) với \(x > - 1\); b. \(\frac{3}{{\sqrt x - 2}}\) với \(x > 0;x \ne 4\); c. \(\frac{{\sqrt 3 - \sqrt 5 }}{{\sqrt 3 + \sqrt 5 }}\); d. \(\frac{{x_{}^2 - 9}}{{\sqrt x - \sqrt 3 }}\) với \(x > 0;x \ne 3\). Phương pháp: + Tìm biểu thức cỏ thể làm mất căn ở mẫu; + Nhân cả tử và mẫu với biểu thức vừa tìm; + Rút gọn biểu thức. Lời giải:
Bài 5 trang 72 SGK Toán 9 tập 1 - Cánh Diều So sánh: a. \(2\sqrt 3 \) và \(3\sqrt 2 \); b. \(7\sqrt {\frac{3}{7}} \) và \(\sqrt 2 .\sqrt {11} \); c. \(\frac{2}{{\sqrt 5 }}\) và \(\frac{6}{{\sqrt {10} }}\). Phương pháp: + Bình phương các số; + So sánh các bình phương; + Kết luận bài toán. Lời giải:
Bài 6 trang 72 SGK Toán 9 tập 1 - Cánh Diều Cho biểu thức: \(M = \frac{{a\sqrt a + b\sqrt b }}{{\sqrt a + \sqrt b }}\) với \(a > 0,b > 0\). a. Rút gọn biểu thức M. b. Tính giá trị của biểu thức tại \(a = 2,b = 8\). Phương pháp: Dùng các kiến thức về đưa thừa số vào trong căn bậc hai để xử lý bài toán. Lời giải: a) Với a > 0, b > 0, ta có:
b) Thay a = 2, b = 8 vào biểu thức
Vậy M = 6 khi a = 2, b = 8. Bài 7 trang 72 SGK Toán 9 tập 1 - Cánh Diều Cho biểu thức: \(N = \frac{{x\sqrt x + 8}}{{x - 4}} - \frac{{x + 4}}{{\sqrt x - 2}}\) với \(x \ge 0,x \ne 4\). a. Rút gọn biểu thức N. b. Tính giá trị của biểu thức tại \(x = 9\). Phương pháp: Dùng các kiến thức về trục căn thức ở mẫu để xử lý bài toán. Lời giải: a) Với x ≥ 0 và x ≠ 4, ta có:
Vậy với x ≥ 0 và x ≠ 4 thì b) Thay x = 9 (thỏa mãn điều kiện) vào biểu thức N, ta được:
Vậy N = –6 khi x = 9. Bài 8 trang 73 SGK Toán 9 tập 1 - Cánh Diều Ngày 28/9/2018, sau trận động đất 7,5 độ Richter, cơn sóng thần (Tiếng Anh là Tsunami) cao hơn 6m đã tràn vào đảo Sulawesicuar (Indonesia) và tàn phá thành phố Palu gây thiệt hại vô cùng to lớn. Tốc độ cơn sóng thần v (m/s) và chiều sâu đại dương d (m) của nơi bắt đầu sóng thần liên hệ bởi công thức \(v = \sqrt {dg} \), trong đó \(g = 9,81\,\,m/s_{}^2\).
a. Hãy tính tốc độ cơn sóng thần xuất phát từ Thái Bình Dương, ở độ sâu trung bình 400m (làm tròn kết quả đến hàng phần trăm của mét trên giây). b. Theo tính toán của các nhà khoa học địa cất, tốc độ cơn sóng thần ngày 28/9/2018 là 800km/h, hãy tính chiều sâu đại dương của nơi tâm chấn động đất gây ra sóng thần (làm tròn kết quả đến hàng đơn vị của mét). Phương pháp: Thay số vào công thức để tìm ra yêu cầu của bài toán. Lời giải: a) Tốc độ cơn sóng thần xuất phát từ Thái Bình Dương, ở độ sâu trung bình 400 m là: Vậy chiều sâu đại dương của nơi tâm chấn động đất gây ra sóng thần là khoảng 5 034 m. Bài 9 trang 73 SGK Toán 9 tập 1 - Cánh Diều Khi bay vào không gian, trọng lượng P(N) của một phi hành gia ở vị trí cách mặt đất một độ cao h(m) được tính theo công thức: \(P = \frac{{28014.10_{}^{12}}}{{\left( {64.10_{}^5 + h} \right)_{}^2}}\). a. Trọng lượng của phi hành gia là bao nhiêu Newton khi cách mặt đất 10 000 m (làm tròn kết quả đến hàng phần mười)? b. Ở độ cao bao nhiêu mét thì trọng lượng của phi hành gia là 619N (làm tròn kết quả đến hàng phần mười)? Phương pháp: Thay số vào công thức để tìm ra yêu cầu bài toán. Lời giải: a) Trọng lượng của phi hành gia khi cách mặt đất 10 000 m là:
Vậy ở độ cao khoảng 327 322,3 mét thì trọng lượng của phi hành gia là 619 N. Bài 10 trang 73 SGK Toán 9 tập 1 - Cánh Diều Áp suất \(P\left( {{\mathop{\rm l}\nolimits} b/in_{}^2} \right)\) cần thiết để ép nước qua một ống dài \(L\left( {ft} \right)\) và đường kính \(d\left( {in} \right)\) với tốc độ \(v\left( {ft/s} \right)\) được cho bởi công thức: \(P = 0,00161.\frac{{v_{}^2L}}{d}\). a. Hãy tính v theo P, L và d. b. Cho \(P = 198,5;\,\,L = 11560;\,\,d = 6\). Hãy tính tốc độ v (làm tròn kết quả đến hàng đơn vị của feet trên giây). Biết rằng \(1\,\,in = 2,54cm;\,\,1\,\,ft\left( {feet} \right) = 0,3048m;\,\,1\,\,lb\left( {pound} \right) = 0,45359237kg;\,\,\) \(1\,\,lb/in_{}^2 = 6894,75729Pa\left( {Pascal} \right)\). Phương pháp: Thay số vào công thức để tính. Lời giải:
b) Tốc độ khi P = 198,5; L = 11 560; d = 6 là:
Vậy v ≈ 8 ft/s. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 3
|

 Tải ngay
Tải ngay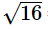 = 4 và –4 là các căn bậc hai của 16.
= 4 và –4 là các căn bậc hai của 16.