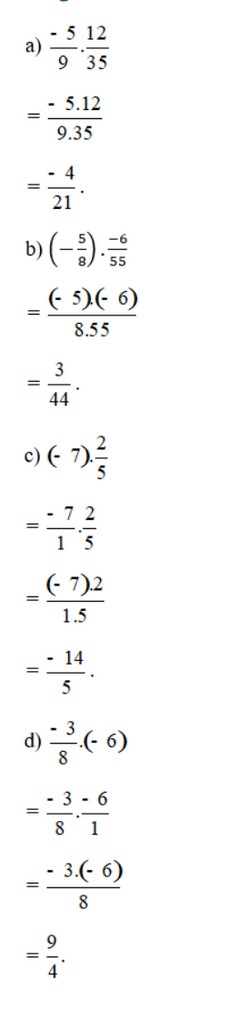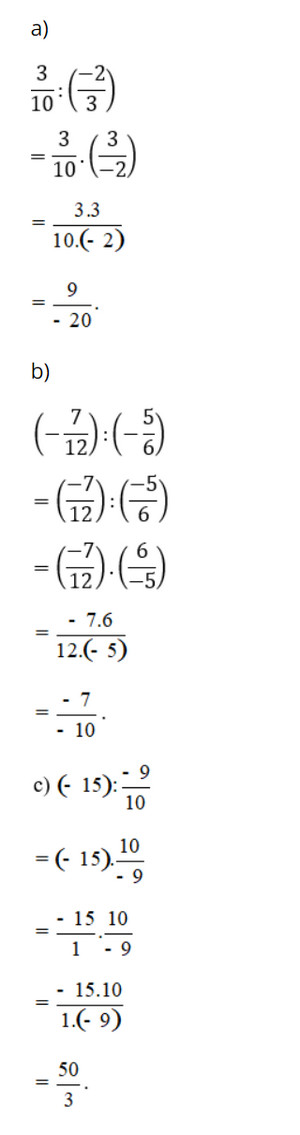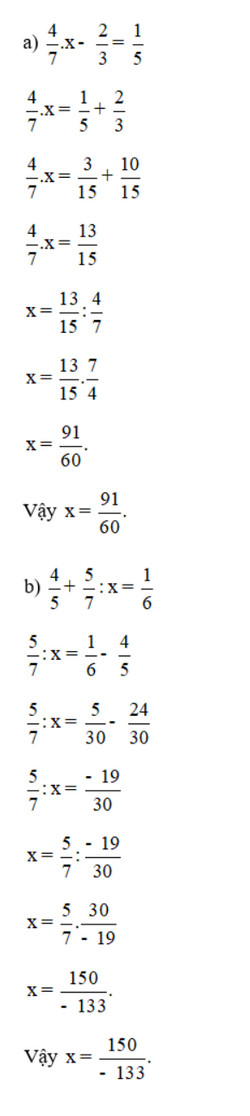Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 43 SGK Toán 6 tập 2 Cánh DiềuGiải SGK Toán lớp 6 trang 43 tập 1 Cánh Diều - Bài 4. Phép nhân, phép chia phân số. Bài 1. Tính tích và viết kết quả ở dạng phân số tối giản. Bài 3. Tìm phân số nghịch đảo của mỗi phân số sau. Bài 1 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tính tích và viết kết quả ở dạng phân số tối giản: a) \(\frac{{ - 5}}{9}.\frac{{12}}{{35}}\); b) \(\left( {\frac{{ - 5}}{8}} \right).\frac{{ - 6}}{{55}}\) c) \(\left( { - 7} \right).\frac{2}{5}\); d) \(\frac{{ - 3}}{8}.\left( { - 6} \right)\) Phương pháp: \(\frac{a}{b}.\frac{c}{d} = \frac{{a.c}}{{b.d}}\) với \(b,d \ne 0\) \(a.\frac{b}{c} = \frac{{a.b}}{c}\) với \(c \ne 0\) Lời giải:
Bài 2 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tìm số thích hợp cho [?]: a) \(\frac{{ - 2}}{3}.\frac{{\left[ ? \right]}}{4} = \frac{1}{2}\); b) \(\frac{{\left[ ? \right]}}{3}.\frac{5}{8} = \frac{{ - 5}}{{12}}\); c) \(\frac{5}{6}.\frac{3}{{\left[ ? \right]}} = \frac{1}{4}.\) Phương pháp: +) Muốn tìm thừa số ta lấy tích chia cho thừa số còn lại. +) Nếu 2 phân số bằng nhau có cùng mẫu số thì tử số của chúng bằng nhau. Lời giải: a) \(\begin{array}{l}\frac{{ - 2}}{3}.\frac{{\left[ ? \right]}}{4} = \frac{1}{2}\\\frac{{\left[ ? \right]}}{4} = \frac{1}{2}:\left( {\frac{{ - 2}}{3}} \right)\\\frac{{\left[ ? \right]}}{4} = \frac{1}{2}.\frac{{ - 3}}{2}\\\frac{{\left[ ? \right]}}{4} = \frac{{ - 3}}{4}\\ \Rightarrow \left[ ? \right] = - 3\end{array}\) b) \(\begin{array}{l}\frac{{\left[ ? \right]}}{3}.\frac{5}{8} = \frac{{ - 5}}{{12}}\\\frac{{\left[ ? \right]}}{3} = \frac{{ - 5}}{{12}}:\frac{5}{8}\\\frac{{\left[ ? \right]}}{3} = \frac{{ - 5}}{{12}}.\frac{8}{5}\\\frac{{\left[ ? \right]}}{3} = \frac{{ - 2}}{3}\\ \Rightarrow \left[ ? \right] = - 2\end{array}\) c) \(\begin{array}{l}\frac{5}{6}.\frac{3}{{\left[ ? \right]}} = \frac{1}{4}\\\frac{3}{{\left[ ? \right]}} = \frac{1}{4}:\frac{5}{6}\\\frac{3}{{\left[ ? \right]}} = \frac{1}{4}.\frac{6}{5}\\\frac{3}{{\left[ ? \right]}} = \frac{3}{{10}}\\ \Rightarrow \left[ ? \right] = 10\end{array}\) Bài 3 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tìm phân số nghịch đảo của mỗi phân số sau: a) \(\frac{{ - 9}}{{19}}\); b) \( - \frac{{21}}{{13}}\); c) \(\frac{1}{{ - 9}}\). Phương pháp: Phân số nghịch đảo của phân số \(\frac{a}{b}\) là \(\frac{b}{a}\) (\({\rm{a,b}} \ne {\rm{0}}\)). Lời giải: a) \(\frac{{ - 19}}{9}\); b) \( - \frac{{13}}{{21}}\); c) \(\frac{{ - 9}}{1} = - 9\) Bài 4 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tính thương và viết kết quả ở dạng phân số tối giản: a) \(\frac{3}{{10}}:\left ({\frac{{ - 2}}{3}} \right)\); b) \(\left( { - \frac{7}{{12}}} \right):\left( { - \frac{5}{6}} \right)\) c) \(\left( { - 15} \right):\frac{{ - 9}}{{10}}\). Phương pháp: \(\frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{a.d}}{{b.c}};\,\,\,\,b,c,d \ne 0\) Lời giải:
Bài 5 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tìm số thích hợp cho [?]: a) \(\frac{3}{{16}}:\frac{{\left[ ? \right]}}{8} = \frac{3}{4}\); b) \(\frac{1}{{25}}:\frac{{ - 3}}{{\left[ ? \right]}} = \frac{{ - 1}}{{15}}\); c) \(\frac{{\left[ ? \right]}}{{12}}:\frac{{ - 4}}{9} = \frac{{ - 3}}{{16}}\). Phương pháp: - Muốn tìm số bị chia ta lấy thương nhân với số chia - Muốn tìm số chia ta lấy số bị chia chia cho thương. Lời giải: a) \(\begin{array}{l}\frac{3}{{16}}:\frac{{\left[ ? \right]}}{8} = \frac{3}{4}\\\frac{{\left[ ? \right]}}{8} = \frac{3}{{16}}:\frac{3}{4}\\\frac{{\left[ ? \right]}}{8} = \frac{3}{{16}}.\frac{4}{3}\\\frac{{\left[ ? \right]}}{8} = \frac{{12}}{{48}}\\\frac{{\left[ ? \right]}}{8} = \frac{2}{8}\\ \Rightarrow \left[ ? \right] = 2\end{array}\) b) \(\begin{array}{l}\frac{1}{{25}}:\frac{{ - 3}}{{\left[ ? \right]}} = \frac{{ - 1}}{{15}}\\\frac{{ - 3}}{{\left[ ? \right]}} = \frac{1}{{25}}:\frac{{ - 1}}{{15}}\\\frac{{ - 3}}{{\left[ ? \right]}} = \frac{1}{{25}}.\frac{{ - 15}}{1}\\\frac{{ - 3}}{{\left[ ? \right]}} = \frac{{ - 15}}{{25}}\\\frac{{ - 3}}{{\left[ ? \right]}} = \frac{{ - 3}}{5}\\ \Rightarrow \left[ ? \right] = 5\end{array}\) c) \(\begin{array}{l}\frac{{\left[ ? \right]}}{{12}}:\frac{{ - 4}}{9} = \frac{{ - 3}}{{16}}\\\frac{{\left[ ? \right]}}{{12}} = \frac{{ - 3}}{{16}}.\frac{{ - 4}}{9}\\\frac{{\left[ ? \right]}}{{12}} = \frac{{12}}{{144}}\\\frac{{\left[ ? \right]}}{{12}} = \frac{1}{{12}}\\ \Rightarrow \left[ ? \right] = 1\end{array}\) Bài 6 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tìm x, biết: a) \(\frac{4}{7}.x - \frac{2}{3} = \frac{1}{5}\); b) \(\frac{4}{5} + \frac{5}{7}:x = \frac{1}{6}\). Phương pháp: - Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ - Muốn tìm số hạng ta lấy tổng trừ đi số hạng còn lại. Lời giải:
Bài 7 trang 43 SGK Toán 6 tập 2 - Cánh Diều Tính: a) \(\frac{{17}}{8}:\left( {\frac{{27}}{8} + \frac{{-11}}{2}} \right)\); b) \(\frac{{28}}{{15}}.\frac{1}{{{4^2}}}.3 + \left( {\frac{8}{{15}} - \frac{{69}}{{60}}.\frac{5}{{23}}} \right):\frac{{-51}}{{54}}\). Phương pháp: Thực hiện phép tính theo thứ tự trong ngoặc => Nhân, chia => Cộng, trừ Lời giải: a) \(\begin{array}{l}\dfrac{{17}}{8}:\left( {\dfrac{{27}}{8} + \dfrac{{-11}}{2}} \right)\\ = \dfrac{{17}}{8}:\left( {\dfrac{{27}}{8} + \dfrac{{-44}}{8}} \right)\\ = \dfrac{{17}}{8}:\dfrac{{-17}}{8}\\ = \dfrac{{17}}{8}.\dfrac{-8}{{17}}\\ =-1\end{array}\) b) \(\begin{array}{l}\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{-51}}{{54}}\\ = \dfrac{{28.1.3}}{{{{15.4}^2}}} + \left( {\dfrac{8}{{15}} - \dfrac{{23.3}}{{4.3.5}}.\dfrac{5}{{23}}} \right).\dfrac{{-54}}{{51}}\\ = \dfrac{{7.4.1.3}}{{3.5.4.4}} + \left( {\dfrac{8}{{15}} - \dfrac{1}{4}} \right).\dfrac{{-54}}{{51}}\\ = \dfrac{7}{{20}} + \left( {\dfrac{{32}}{{60}} - \dfrac{{15}}{{60}}} \right).\dfrac{{-54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{60}}.\dfrac{{-54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{6.10}}.\dfrac{{-6.3.3}}{{17.3}}\\ = \dfrac{7}{{20}} + \dfrac{-3}{{10}}\\ = \dfrac{7}{{20}} + \dfrac{-6}{{20}}\\ = \dfrac{{1}}{{20}}\end{array}\) Bài 8 trang 43 SGK Toán 6 tập 2 - Cánh Diều Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp \(\frac{{33}}{8}\) lần chim ruồi ong. Tính chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ.
Phương pháp: Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ = \(\frac{{33}}{8}\). Chiều dài của chim ruồi ong. Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài 4. Phép nhân, phép chia phân số
|
-

Giải bài 1, 2, 3, 4, 5 trang 47 SGK Toán 6 tập 2 Cánh Diều
Giải SGK Toán lớp 6 trang 47 tập 1 Cánh Diều - Bài 5. Số thập phân. Bài 5. Trong một cuộc thi chạy 200 m, có ba vận động viên đạt thành tích cao nhất là: Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây. Vận động viên nào đã về nhất? Về nhì? Về ba?

 Tải ngay
Tải ngay