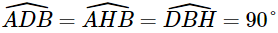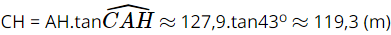Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 87 SGK Toán 9 Cánh Diều tập 1Hình 26 minh hoạ một phần con sông có bề rộng (AB = 100m).Một chiếc thuyền đi thẳng từ vị trí (B) bên này bờ sông đến vị trí (C) bên kia bờ sông. Tính quãng đường (BC) (làm tròn kết quả đến hàng phần mười của mét), biết (widehat {ABC} = 35^circ ). Bài 1 trang 86 SGK Toán 9 tập 1 - Cánh Diều Tìm \(x,y\) trong mỗi hình \(23a,23b,23c\) (làm tròn kết quả đến hàng phần mười của centimét)
Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải: a) Từ hình ta có: ⦁ x = 6.cos56° ≈ 3,4 (cm). ⦁ y = 6.sin56° ≈ 5,0 (cm). b) Từ hình ta có: ⦁ x = 1,5.cot32° ≈ 2,4 (cm). ⦁ 1,5 = y.sin32°, suy ra c) Từ hình ta có: ⦁ 0,8 = x.cos70°, suy ra ⦁ y = 0,8.tan70° ≈ 2,2 (cm). Bài 2 trang 86 SGK Toán 9 tập 1 - Cánh Diều Cho tam giác \(ABC\) có đường cao \(AH = 6cm,\widehat B = 40^\circ ,\widehat C = 35^\circ \). Tính độ dài các đoạn thẳng \(AB,BH,AC,BC\) (làm tròn kết quả đến hàng phần mười của centimét). Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải:
Xét ∆ABH vuông tại H, ta có: ⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).
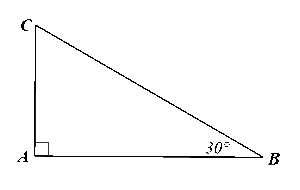
Xét ∆ACH vuông tại H, ta có: ⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm). Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm). Bài 3 trang 86 SGK Toán 9 tập 1 - Cánh Diều Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = 30^\circ \). Chứng minh \(AC = \frac{1}{2}BC\). Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải:
Xét ∆ABC vuông tại A, ta có: AC = BC.sinB = BC.sin30o = Vậy AC = Bài 4 trang 87 SGK Toán 9 tập 1 - Cánh Diều Cho tam giác \(ABC\) vuông cân tại \(A\). Chứng minh \(AB = AC = \frac{{\sqrt 2 }}{2}BC\). Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải:
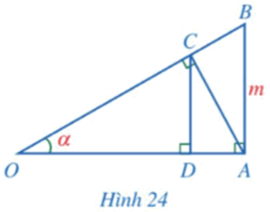
Bài 5 trang 87 SGK Toán 9 tập 1 - Cánh Diều Trong Hình 24, cho \(\widehat O = \alpha ,AB = m\) và \(\widehat {OAB} = \widehat {OCA} = \widehat {ODC} = 90^\circ \).
Chứng minh: a) \(OA = m.\cot \alpha \); b) \(AC = m.\cos \alpha \); c) \(CD = m.{\cos ^2}\alpha \). Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải: a) Xét ∆OAB vuông tại A, ta có: OA = AB.cotO = m.cotα. b) Xét ∆OAC vuông tại C, ta có:
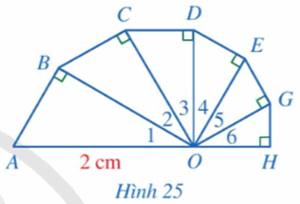
Bài 6 trang 87 SGK Toán 9 tập 1 - Cánh Diều Tính độ dài đường gấp khúc \(ABCDEGH\), biết các tam giác \(OAB,OBC,OCD,ODE,OEG,OGH\) là các tam giác vuông tại các đỉnh lần lượt là \(B,C,D,E,G,H\); các góc \({O_1},{O_2},{O_3},{O_4},{O_5},{O_6}\) đều bằng \(30^\circ \) và \(OA = 2cm\) (Hình 25).
Chứng minh: a) \(OA = m.\cot \alpha \); b) \(AC = m.\cos \alpha \); c) \(CD = m.{\cos ^2}\alpha \). Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải:
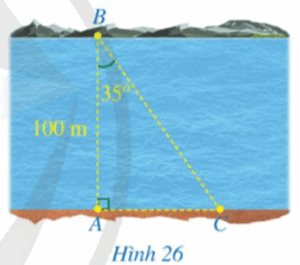
Bài 7 trang 87 SGK Toán 9 tập 1 - Cánh Diều Hình 26 minh hoạ một phần con sông có bề rộng \(AB = 100m\).Một chiếc thuyền đi thẳng từ vị trí \(B\) bên này bờ sông đến vị trí \(C\) bên kia bờ sông. Tính quãng đường \(BC\) (làm tròn kết quả đến hàng phần mười của mét), biết \(\widehat {ABC} = 35^\circ \).
Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải: Xét ∆ABC vuông tại A, ta có:
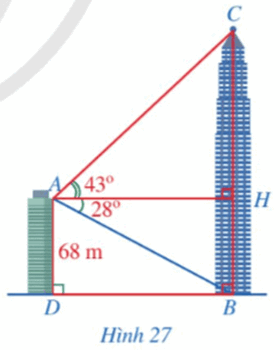
Bài 8 trang 87 SGK Toán 9 tập 1 - Cánh Diều Từ vị trí \(A\) ở phía trên một tòa nhà có chiều cao \(AD = 68m\), bác Duy nhìn thấy vị trí \(C\) cao nhất của một tháp truyền hình, góc tạo bởi tia \(AC\) và tia \(AH\) theo phương nằm ngang là \(\widehat {CAH} = 43^\circ \). Bác Duy cũng nhìn thấy chân tháp tại vị trí \(B\) mà góc tạo bởi tia \(AB\) và tia \(AH\) là \(\widehat {BAH} = 28^\circ \), điểm \(H\) thuộc đoạn \(BC\) (Hình 27). Tính khoảng cách \(BD\) từ chân tháp đến chân tòa nhà và chiều cao \(BC\) của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp: Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải: Vì AH ⊥ BC và BD ⊥ BC nên AH // BD. Do đó Khoảng cách BD từ chân tháp đến chân tòa nhà là:
Do tứ giác ADBH có Suy ra AH = DB ≈ 127, 9 (m) và HB = AD = 68 (m). Do ∆AHC vuông tại H, ta có Chiều cao BC của tháp truyền hình là: BC = BH + HC ≈ 68 + 119,3 = 187,3 (m). Vậy khoảng cách BD từ chân tháp đến chân tòa nhà khoảng 127,9 mét và chiều cao BC của tháp truyền hình khoảng 187,3 mét. Sachbaitap.com
Xem thêm tại đây:
Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông
|
-

Giải bài 1, 2, 3, 4, 5 trang 90, 91 SGK Toán 9 Cánh Diều tập 1
Một mảnh gỗ có dạng hình chữ nhật (ABCD) với đường chéo (AC = 8dm). Do bảo quản không tốt nên mảnh gỗ bị hỏng phía hai đỉnh (B) và (D). Biết (widehat {BAD} = 64^circ ) (Hình 38). Người ta cần biết độ dài (AB) và (AD) để khôi phục mảnh gỗ ban đầu. Độ dài (AB,AD) bằng bao nhiêu decimét (làm tròn kết quả đến hàng phần mười)?

 Tải ngay
Tải ngay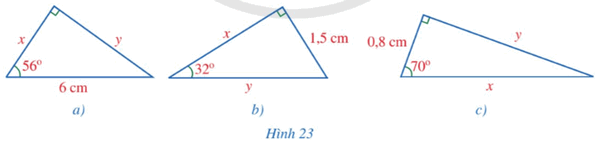

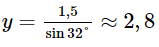
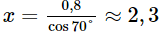 (cm)
(cm)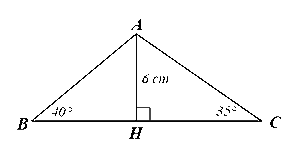
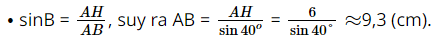
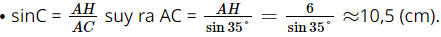
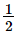 BC
BC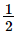 BC.
BC. 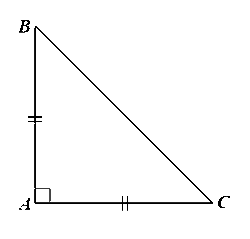
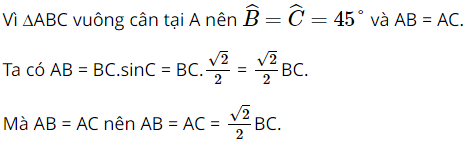



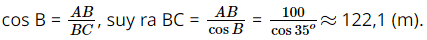
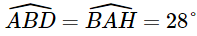 (so le trong).
(so le trong).