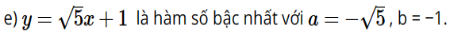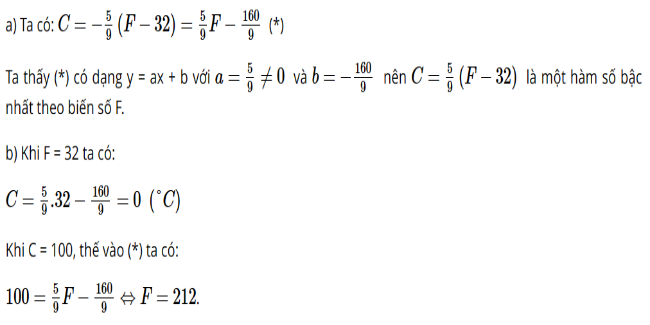Giải bài 1, 2, 3, 4, 5, 6 trang 22 SGK Toán 8 Chân trời sáng tạo tập 2

Bài 1 trang 22 SGK Toán 8 tập 2 - Chân trời sáng tạo

Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số \(a,b\) của chúng.

a) \(y = 4x + 2\);                  b) \(y = 5 - 3x\);                            c) \(y = 2 + {x^2}\);

d) \(y =  - 0,2x\);                  e) \(y = \sqrt 5 x - 1\).

Phương pháp:

Dựa vào định nghĩa hàm số bậc nhất: Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\) với \(a,b\) là các số cho trước và \(a \ne 0\).

Lời giải:

a) y = 4x + 2 là hàm số bậc nhất với a = 4, b = 2.

b) y = 5 – 3x là hàm số bậc nhất với a = −3, b = 5

c) y= 2 + x² không là hàm số bậc nhất.

d) y = −0,2x là hàm số bậc nhất với a = y = −0,2, b = 0.

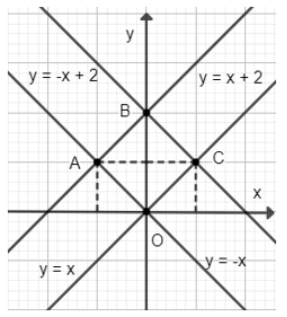
Bài 2 trang 22 SGK Toán 8 tập 2 - Chân trời sáng tạo

Với giá trị nào của \(m\) thì mỗi hàm số sau đây là hàm số bậc nhất?

a) \(y = \left( {m - 1} \right)x + m\);                        b) \(y = 3 - 2mx\).

Phương pháp:

Hàm số \(y = ax + b\) là hàm số bậc nhất nếu \(a \ne 0\).

Lời giải:

a) Điều kiện để hàm số y = (m − 1)x + m là hàm số bậc nhất là m − 1 ≠ 0 hay m ≠ 1.

b) Điều kiện để hàm số y = 3 − 2mx là hàm số bậc nhất là −2m ≠ 0 hay m ≠ 0.

Bài 3 trang 22 SGK Toán 8 tập 2 - Chân trời sáng tạo

a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:

\(y = x\);        \(y = x + 2\);              \(y =  - x\)                 \(y =  - x + 2\).

b) Bốn đồ thị nói trên cắt nhau tại các điểm \(O\left( {0;0} \right),A,B,C\). Tứ giác có bốn đỉnh \(O;A;B;C\) là hình gì?

Giải thích.

Phương pháp:

a) - Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:

Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).

Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:

Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(A\left( {0;b} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(B\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).

Bước 2: Vẽ đường thẳng đi qua hai điểm \(A\) và \(B\). Đồ thị của hàm số \(y = ax + b\) là đường thẳng đi qua hai điểm \(A\) và \(B\).

- Đồ thị hàm số \(y = ax + b\) là một đường thẳng và song song với đường thẳng \(y = ax\).

b) 

Tính độ dài các cạnh và góc của tứ giác.

Chú ý: Hình thoi có 1 góc vuông là hình vuông.

Lời giải:

a) 

a) Với hàm số y = x, cho x = 1 thì y = 1.

Đồ thị hàm số y = x đi qua các điểm O(0; 0) và C(1; 1).

Với hàm số y = x + 2, cho x = 0 thì y = 2, cho x = −1 thì y = 1.

Đồ thị hàm số y = x + 2 đi qua các điểm B(0; 2) và A(−1; 1).

Với hàm số y = −x, cho x = −1 thì y = 1.

Đồ thị hàm số y = −x đi qua các điểm O(0; 0) và A(−1; 1).

Với hàm số y = −x + 2, cho x = 0 thì y = 2, cho x = 1 thì y = 1.

Đồ thị hàm số y = −x + 2 đi qua các điểm B (0; 2) và C(1; 1).

b) Ta có: Đường thẳng y = x song song với đường thẳng y = x + 2 suy ra OC // AB.

Đường thẳng y = −x song song với đường thẳng y = −x + 2 suy ra OA // BC.

Tứ giác OABC có: OC // AB, OA // BC

Suy ra tứ giác OABC là hình bình hành.

Hình bình hành OABC có hai đường chéo OB và AC vuông góc và bằng nhau nên tứ giác OABC là hình vuông.

Bài 4 trang 22 SGK Toán 8 tập 2 - Chân trời sáng tạo

Để đổi nhiệt độ từ \(F\) (Fahrenheit) sang độ \(C\) (Celsius), ta dùng công thức \(C = \dfrac{5}{9}.\left( {F - 32} \right)\).

a) \(C\) có phải hàm số bậc nhất theo biến số \(F\) không?

b) Hãy tính \(C\) khi \(F = 32\) và tính \(F\) khi \(C = 100\).

Phương pháp:

Dựa vào định nghĩa hàm số bậc nhất: Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\) với \(a,b\) là các số cho trước và \(a \ne 0\).

Lời giải:

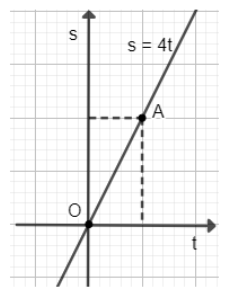
Bài 5 trang 22 SGK Toán 8 tập 2 - Chân trời sáng tạo

Gọi \(C\) và \(r\) lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ \(C\) là một hàm số bậc nhất theo biến số \(r\). Tìm hệ số \(a,b\) của hàm số này.

Phương pháp:

- Công thức tính chu vi đường tròn:

\(C = \pi .d = \pi .2r\) (đơn vị độ dài)

- Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\) với \(a,b\) là các số cho trước và \(a \ne 0\).

Lời giải:

Công thức tính chu vi hình tròn là: C = 2πr

Hàm số C = 2πr có dạng y = ax + b với a = 2π ≠ 0 và b = 0 nên C là một hàm số bậc nhất theo biến số r.

Bài 6 trang 22 SGK Toán 8 tập 2 - Chân trời sáng tạo

a) Lập công thức tính \(s\) theo \(t\).

b) Vẽ đồ thị của hàm số \(s\) theo \(t\) khi \(v = 4\).

Phương pháp:

a) - Công thức tính quãng đường: \(s = v.t\)

b) - Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:

Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).

Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và

\(M\).

Lời giải:

a) s = vt.

Đồ thị hàm số s = 4t là đường thẳng đi qua 2 điểm O(0; 0); A(1; 4).

Sachbaitap.com