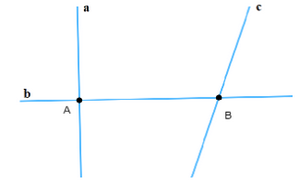
Giải bài 1, 2, 3, 4, 5 trang 73 SGK Toán 6 tập 2 Chân trời sáng tạo

Bài 1 trang 73 SGK Toán 6 tập 2 - Chân trời sáng tạo

a) Hãy đặt tên cho các điểm và đường thẳng trong hình dưới đây.

b) Hãy nêu ba cách gọi tên đường thẳng trong hình dưới đây.

Phương pháp:

Đường thẳng được đặt tên bởi chữ in thường như: a, b, c, x, y…

Điểm được đặt tên bởi chữ in hoa: A, B, C, D,…

- Đường thẳng có thể được gọi tên bằng hai điểm thuộc đường thẳng.

Lời giải:

a) Đường thẳng được đặt tên bởi chữ in thường như: a, b, c, x, y…

Điểm được đặt tên bởi chữ in hoa: A, B, C, D,…

Chẳng hạn: ta đặt tên các điểm là A, B và các đường thẳng là a, b, c. 

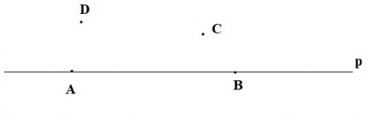
b) Ta có thể gọi tên đường thẳng bằng cách:

- Gọi theo tên đường thẳng, thường được đặt bằng chữ cái thường a, b, c..

- Gọi tên bằng hai điểm thuộc đường thẳng.

Ba cách gọi tên đường thẳng trong hình trên là: đường thẳng AB đường thẳng BD và đường thẳng CD (có thể chọn các điểm khác sẽ có các cách gọi khác).

Bài 2 trang 73 SGK Toán 6 tập 2 - Chân trời sáng tạo

Dùng kí hiệu để biểu thị các mối quan hệ dưới đây và vẽ các hình tương ứng.

a) Các điểm A, B thuộc đường thẳng p.

b) Các điểm C, D không thuộc đường thẳng p.

Phương pháp:

Điểm thuộc đường thẳng ta dùng kí hiệu: ∈

Điểm không thuộc đường thẳng ta dùng kí hiệu: ∉ 

Lời giải:

a) A, B  ∈ p

b) C, D ∉ p

Vẽ hình:

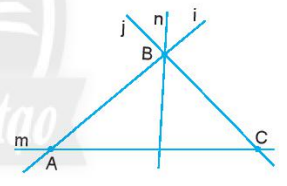
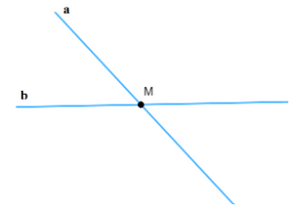
Bài 3 trang 73 SGK Toán 6 tập 2 - Chân trời sáng tạo

Trong hình vẽ bên:

a) Điểm B thuộc những đường thẳng nào?

b) Điểm A không thuộc những đường thẳng nào?

Sử dụng kí hiệu để mô tả các quan hệ trên.

Phương pháp:

Quan sát hình vẽ và trả lời câu hỏi.

Điểm thuộc đường thẳng ta dùng kí hiệu: ∈

Điểm không thuộc đường thẳng ta dùng kí hiệu: ∉ 

Lời giải:

a) Điểm B thuộc đường thẳng j, n, i hay: B ∈ j, B ∈ n, B∈ i

b) Điểm A không thuộc đường thẳng j và n hay: A ∉ j, A∉  n

c) Đường thẳng i và n không chứa điểm C hay C ∉ i, C ∉ n.

Bài 4 trang 73 SGK Toán 6 tập 2 - Chân trời sáng tạo

Vẽ hình cho mỗi trường hợp sau:

a) Điểm M thuộc đường thẳng a.

b) Điểm M thuộc hai đường thẳng a và b nhưng không thuộc đường thẳng c.

c) Điểm M nằm trên cả ba đường thẳng a, b và c.

Phương pháp:

Vẽ hình theo phát biểu của đề bài.

Lời giải:

a) Cách vẽ điểm M thuộc đường thẳng a:

Cách 1: Vẽ điểm M trước rồi vẽ đường thẳng a.

Chấm một điểm M bất kỳ.

- Vẽ đường thẳng a đi qua điểm M. Ta được điểm M thuộc đường thẳng a.

Ta có hình vẽ:

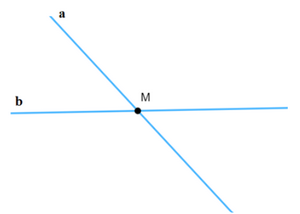
Cách 2: Vẽ đường thẳng a trước rồi vẽ điểm M.

- Vẽ đường thẳng a bất kỳ.

- Lấy điểm M nằm trên đường thẳng a.

- Vẽ đường thẳng a đi qua điểm M. Ta được điểm M thuộc đường thẳng a.

Ta có hình vẽ:

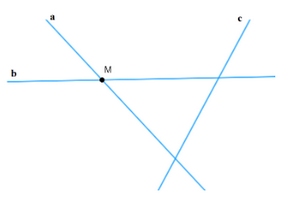
b) Điểm M thuộc hai đường thẳng a và b nhưng không thuộc đường thẳng c.

* Cách vẽ:

Bước 1: Vẽ hai đường thẳng a và b cắt nhau tại điểm M (như hình vẽ).

Bước 2: Vẽ đường thẳng c không đi qua điểm M. Ta được điểm M thuộc hai đường thẳng a và b nhưng không thuộc đường thẳng c.

* Ta có hình vẽ:

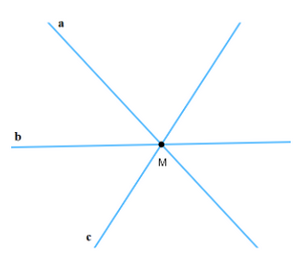
c) Điểm M nằm trên cả ba đường thẳng a, b và c.

* Cách vẽ:

Bước 1: Vẽ hai đường thẳng a và b cắt nhau tại điểm M (như hình vẽ).

Bước 2: Vẽ đường thẳng c không đi qua điểm M. Ta được điểm M nằm trên cả ba đường thẳng a, b và c.

* Ta có hình vẽ:

Bài 5 trang 73 SGK Toán 6 tập 2 - Chân trời sáng tạo

Hãy nêu một số hình ảnh của đường thẳng và điểm thuộc (không thuộc) đường thẳng trong thực tế.

Phương pháp:

Em nêu một số hình ảnh của đường thẳng và điểm thuộc (không thuộc) đường thẳng trong thực tế mà em thấy.

Lời giải:

Một số hình ảnh của đường thẳng và điểm thuộc (không thuộc) đường thẳng trong thực tế là:

- Hình ảnh của đường thẳng: 

+ Dây điện ở các cột điện cao áp.

 

+ Ống dẫn nước kéo dài qua rất nhiều nơi.

- Điểm thuộc đường thẳng: Con muỗi đậu trên sợi dây phơi quần áo, giọt nước trên mép bàn.

- Điểm không thuộc đường thẳng: Giọt nước ở dưới sàn và dây phơi quần áo,…

Sachbaitap.com