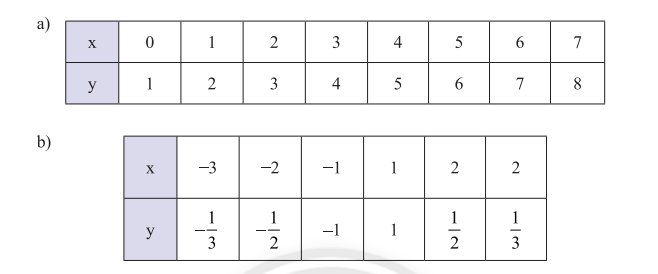
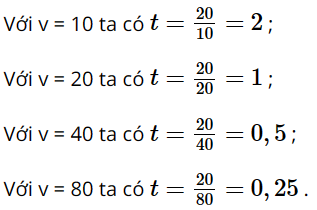Giải bài 1, 2, 3, 4, 5 trang 9 SGK Toán 8 Chân trời sáng tạo tập 2

Bài 1 trang 9 SGK Toán 8 tập 2 - Chân trời sáng tạo

Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.

Phương pháp:

Quan sát các bảng sau đó sử dụng định nghĩa về hàm số để giải thích và đưa ra kết luận

Nếu đại lượng \(y\) phụ thuộc vào một đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được duy nhất một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của biến số \(x\).

Lời giải:

a) Dựa vào bảng, ta thấy với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng, do đó đại lượng y là hàm số của đại lượng x.

b) Dựa vào bảng, ta thấy tồn tại một giá trị của x ta có thể nhận được hai giá trị của y tương ứng, do đó đại lượng y không là hàm số của đại lượng x.

Ví dụ: Khi x = 2 thì y = $\frac{\mathrm{1/2}}{}$ hoặc y = 1/3

Bài 2 trang 9 SGK Toán 8 tập 2 - Chân trời sáng tạo

Cho hàm số \(y = f\left( x \right) = 3x\)

a) Tính \(f\left( 1 \right);f\left( { - 2} \right);f\left( {\dfrac{1}{3}} \right)\).

b) Lập bảng các giá trị tương ứng của \(y\) khi \(x\) lần lượt nhận các giá trị:

\( - 3; - 2; - 1;0;1;2;3\).

Phương pháp:

Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có \(y = f\left( a \right)\) thì \(f\left( a \right)\) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).

Đối với hàm số \(y = f\left( x \right) = 3x\), khi đó, \(x = a \Rightarrow f\left( a \right) = 3a\).

Lời giải:

a) Ta có:

 f(1) = 3.1 = 3;

 f(−2) = 3.(−2) = −6;

b) Ta có f(−3) = 3.(−3) = −9; f(−1) = 3.(−1) = −3;

f(0) = 3.0 = 0; f(2) = 3.2 = 6; f(3) = 3.3 = 9.

Từ đó ta có bảng sau:

Bài 3 trang 9 SGK Toán 8 tập 2 - Chân trời sáng tạo

Cho hàm số \(y = f\left( x \right) = {x^2} + 4\). Tính \(f\left( { - 3} \right);f\left( { - 2} \right);f\left( { - 1} \right);f\left( 0 \right);f\left( 1 \right)\)

Phương pháp:

Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có \(y = f\left( a \right)\) thì \(f\left( a \right)\) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).

Đối với hàm số \(y = f\left( x \right) = {x^2} + 4\), khi đó, \(x = a \Rightarrow f\left( a \right) = {a^2} + 4\).

Lời giải:

f(−3) = (−3)² + 4 = 9 + 4 = 13;

f(−2) = (−2)² + 4 = 4 + 4 = 8;

f(−1) = (−1)² + 4 = 5;

f(0) = 0 + 4 = 4;

f(1) = 1 + 4 = 5.

Vậy f(−3) = 13; f(−2) = 8; f(−1) = 5; f(0) = 4; f(1) = 5.

Bài 4 trang 9 SGK Toán 8 tập 2 - Chân trời sáng tạo

Khối lượng m (g) của một thanh sắt có khối lượng riêng là 7,8 kg/dm³ tỉ lệ thuận với thể tích V (cm³) theo công thức m = 7,8V. Đại lượng m có phải là hàm số của đại lượng V không? Nếu có, tính m(10); m(20); m(40); m(50).

Phương pháp:

Dựa vào định nghĩa về hàm số và giá trị của hàm số.

Lời giải:

Đại lượng m là hàm số của đại lượng V vì với mỗi một giá trị của V ta luôn chỉ xác định được một giá trị của m.

Ta có: m = 7,8V

m(10) = 7,8.10 = 78;

m(20) = 7,8.20 = 156;

m(40) = 7,8.40 = 312;

m(50) = 7,8.50 = 390.

Bài 5 trang 9 SGK Toán 8 tập 2 - Chân trời sáng tạo

Thời gian \(t\)(giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ \(v\) (km/h) của nó theo công thức \(t = \dfrac{{20}}{v}\). Tính và lập bảng các giá trị tương ứng của \(t\) với \(v\) lần lượt nhận các giá trị 10; 20; 40; 80.

Phương pháp:

Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có \(y = f\left( a \right)\) thì \(f\left( a \right)\) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).

Với \(v = a \Rightarrow t\left( a \right) = \dfrac{{20}}{a}\)

Lời giải:

Khi đó, ta có bảng sau:

Sachbaitap.com