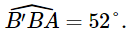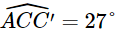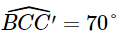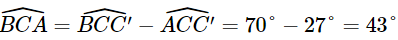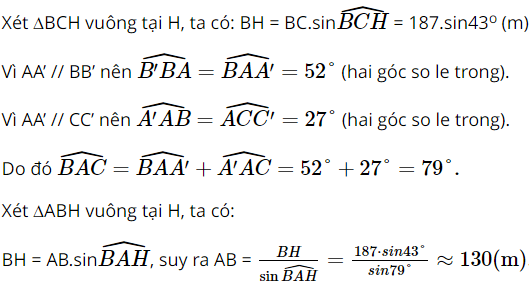Giải bài 1, 2, 3, 4 trang 92 SGK Toán 9 Cánh Diều tập 1Một người đứng ở vị trí (B) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí (A) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:- Sử dụng la bàn, xác định được phương (BA) lệch với phương Nam – Bắc về hướng Đông (52^circ ). Bài 1 trang 92 SGK Toán 9 tập 1 - Cánh Diều Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha \) (Hình 40).
a) Tỉ số \(\frac{{HA}}{{HB}}\) bằng: A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \). b) Tỉ số \(\frac{{HA}}{{HC}}\) bằng: A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \). c) Tỉ số \(\frac{{HA}}{{AC}}\) bằng: A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \). Phương pháp: Dựa vào tỉ số lượng giác để giải bài toán. Lời giải: a) Đáp án đúng là: C Xét ∆ABH vuông tại H, ta có b) Đáp án đúng là: D
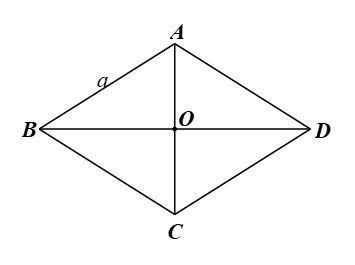
c) Đáp án đúng là: B Bài 2 trang 92 SGK Toán 9 tập 1 - Cánh Diều Cho hình thoi \(ABCD\) có \(AB = a,\widehat {BAD} = 2\alpha \left( {0^\circ < \alpha < 90^\circ } \right)\). Chứng minh: a) \(BD = 2a.\sin \alpha \). b) \(AC = 2a.\cos \alpha \). Phương pháp: Dựa vào tỉ số lượng giác để giải bài toán. Lời giải:
a) Gọi O là giao điểm của đường chéo AC và BD. Vì ABCD là hình thoi nên AC ⊥ BD tại trung điểm O của mỗi đường và AC là đường phân giác của
Do đó AC = 2AO = 2a.cosα. Bài 3 trang 92 SGK Toán 9 tập 1 - Cánh Diều Trong trò chơi xích đu ở Hình 41, khi dây căng xích đu (không dãn) \(OA = 3m\) tạo với phương thẳng đứng một góc là \(\widehat {AOH} = 43^\circ \) thì khoảng cách \(AH\) từ em bé đến vị trí cân bằng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Phương pháp: Dựa vào tỉ số lượng giác để giải bài toán. Lời giải: Xét ∆OAH vuông tại H, ta có: Vậy khoảng cách từ em bé đến vị trí cân bằng khoảng 2 m. Bài 4 trang 92 SGK Toán 9 tập 1 - Cánh Diều Một người đứng ở vị trí \(B\) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí \(A\) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau: - Sử dụng la bàn, xác định được phương \(BA\) lệch với phương Nam – Bắc về hướng Đông \(52^\circ \). - Người đó di chuyển đến vị trí \(C\), cách \(B\) một khoảng là 187m. Sử dụng la bàn, xác định được phương \(CA\) lệch với phương Nam – Bắc về hướng Tây \(27^\circ \); \(CB\) lệch với phương Nam – Bắc về hướng Tây \(70^\circ \) (Hình 42).
Em hãy giúp người đó tính khoảng cách \(AB\) từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).
Dựa vào tỉ số lượng giác để giải bài toán. Lời giải:
Kẻ AA’ (A’ ∈ BC) theo phương Bắc – Nam và kẻ BB’, CC’ theo phương Nam – Bắc (hình vẽ). Khi đó AA’ // BB’ // CC’. Phương BA lệch với phương Nam – Bắc về hướng Đông 52° nên Phương CA lệch với phương Nam – Bắc về hướng Tây 27° nên Phương CB lệch với phương Nam – Bắc về hướng Tây 70° nên Do đó Kẻ BH ⊥ AC (H ∈ AC).
Vậy khoảng cách AB khoảng 130 mét. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 4
|

 Tải ngay
Tải ngay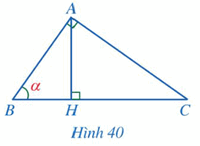

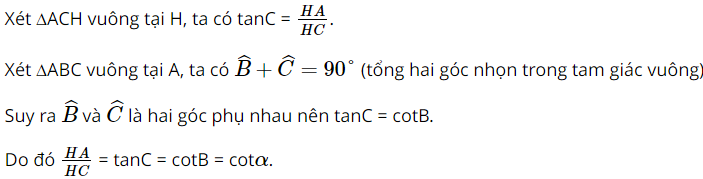


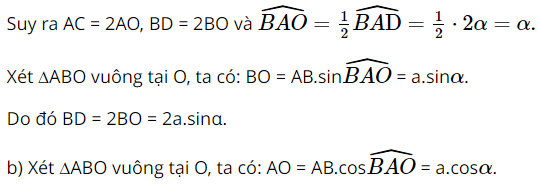


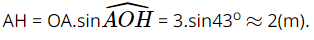

 Phương pháp:
Phương pháp: