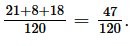Giải bài 1, 2, 3, 4 trang 94 SGK Toán 8 Chân trời sáng tạo tập 2Giải SGK Toán lớp 8 trang 94 Chân trời sáng tạo tập 2. Ở một sân bay người ta nhận thấy với mỗi chuyến bay, xác suất tất cả mọi người đều có mặt để lên máy bay là 0,9. Trong một ngày, sân bay có 120 lượt máy bay cất cánh. Hãy ước lượng số chuyến bay trong ngày hôm đó có người mua vé nhưng không lên máy bay. Bài 1 trang 94 SGK Toán 8 tập 2 - Chân trời sáng tạo Phương gieo một con xúc xắc 120 lần và thống kê lại kết quả các lần gieo ở bảng sau:
Hãy tính xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 120 lần thử trên. Phương pháp: Gọi \(n\left( A \right)\) là số lần xuất hiện biến cố \(A\) khi thực hiện phép thử đó \(n\) lần. Xác suất thực nghiệm của biến cố \(A\) là tỉ số \(\frac{{n\left( A \right)}}{n}\) Lời giải: Ta có những mạt có số chấm lẻ là: 1 chấm; 3 chấm; 5 chấm. Khi đó số kết quả thuận lợi cho biến cố “Gieo được mặt có số chấm lẻ” là: 21 + 8 + 18 = 47. Vậy xác suất thực nghiệm của biến cố "Gieo được mặt có số chấm lẻ":
Bài 2 trang 94 SGK Toán 8 tập 2 - Chân trời sáng tạo Ở một sân bay người ta nhận thấy với mỗi chuyến bay, xác suất tất cả mọi người đều có mặt để lên máy bay là 0,9. Trong một ngày, sân bay có 120 lượt máy bay cất cánh. Hãy ước lượng số chuyến bay trong ngày hôm đó có người mua vé nhưng không lên máy bay. Phương pháp: Gọi \(P\left( A \right)\) là xác suất xuất hiện biến cố \(A\) khi thực hiện một phép thử. Gọi \(n\left( A \right)\) là số lần xuất hiện biến cố \(A\) khi thực hiện phép thử đó \(n\) lần. Xác suất thực nghiệm của biến cố \(A\) là tỉ số \(\frac{{n\left( A \right)}}{n}\) Khi \(n\) càng lớn, xác suất thực nghiệm của biến cố \(A\) càng gần \(P\left( A \right)\). Lời giải:
Suy ra số chuyến bay trong ngày hôm đó có người mua vé nhưng không lên máy bay là khoảng: 120 – 108 = 12. Vậy số chuyến bay trong ngày hôm đó có người mua vé nhưng không lên máy bay là khoảng 12 lượt. Bài 3 trang 94 SGK Toán 8 tập 2 - Chân trời sáng tạo Một hộp chứa các viên bi màu trắng và đen có kích thước và khối lượng như nhau. Mai lấy ra ngẫu nhiên 1 viên bi từ hộp, xem màu rồi trả lại hộp. Lặp lại thử nghiệm đó 80 lần, Mai thấy có 24 lần lấy được viên bi màu trắng. a) Hãy tính xác suất thực nghiệm của biến cố “Lấy được viên bi màu đen” sau 80 lần thử. b) Biết tổng số bi trong hộp là 10. Hãy ước lượng xem trong hộp có khoảng bao nhiêu viên bi trắng. Phương pháp: Gọi \(P\left( A \right)\) là xác suất xuất hiện biến cố \(A\) khi thực hiện một phép thử. Gọi \(n\left( A \right)\) là số lần xuất hiện biến cố \(A\) khi thực hiện phép thử đó \(n\) lần. Xác suất thực nghiệm của biến cố \(A\) là tỉ số \(\frac{{n\left( A \right)}}{n}\) Khi \(n\) càng lớn, xác suất thực nghiệm của biến cố \(A\) càng gần \(P\left( A \right)\). Lời giải:
Bài 4 trang 94 SGK Toán 8 tập 2 - Chân trời sáng tạo Trong một cuộc điều tra, người ta phỏng vấn 300 người được lựa chọn ngẫu nhiên ở một khu dân cư thì thấy có 255 người ủng hộ việc tắt điện trong sự kiện Giờ Trái Đất. Hãy ước lượng xác suất của biến cố “Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ việc tắt đèn điện trong sự kiện Giờ Trái Đất”. Phương pháp: Gọi \(P\left( A \right)\) là xác suất xuất hiện biến cố \(A\) khi thực hiện một phép thử. Gọi \(n\left( A \right)\) là số lần xuất hiện biến cố \(A\) khi thực hiện phép thử đó \(n\) lần. Xác suất thực nghiệm của biến cố \(A\) là tỉ số \(\frac{{n\left( A \right)}}{n}\) Khi \(n\) càng lớn, xác suất thực nghiệm của biến cố \(A\) càng gần \(P\left( A \right)\). Lời giải:
Vì số lượng người được phỏng vấn lớn (300 người) nên xác suất thực nghiệm gần bằng xác suất của biến cố "Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ viêc tắt đèn điện trong sự kiện Giờ Trái Đất”. Vậy xác suất của biến cố "Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ viêc tắt đèn điện trong sự kiện Giờ Trái Đất” bằng khoảng 0,85. Sachbaitap.com
Xem thêm tại đây:
Bài 2. Xác suất lí thuyết và xác suất thực nghiệm
|
-

Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 trang 95, 96 SGK Toán 8 Chân trời sáng tạo tập 2
Giải SGK Toán lớp 8 trang 95, 96 Chân trời sáng tạo tập 2. Tỉ lệ vận động viên đạt huy chương trong một đại hội thể thao là 21%. Gặp ngẫu nhiên một vận động viên dự đại hội. Tính xác suất của biến cố vận động viên ấy đạt huy chương.

 Tải ngay
Tải ngay