Giải bài 2.21, 2.22, 2.23, 2.24, 2.25, 2.26, 2.27, 2.28, 2.29, 2.30, 2.31, 2.32 trang 42 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 42 Kết nối tri thức tập 1. Bài 2.31: Thanh tham dự một kì kiểm tra năng lực tiếng Anh gồm 4 bài kiểm tra nghe, nói, đọc và viết. Mỗi bài kiểm tra có điểm số nguyên từ 0 đến 10. Điểm trung bình của ba bài kiểm tra nghe, nói, đọc của Thanh là 6,7. Bài 2.21 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Nghiệm của bất phương trình \( - 2x + 1 < 0\) là A. \(x < \frac{1}{2}.\) B. \(x > \frac{1}{2}.\) C. \(x \le \frac{1}{2}.\) D. \(x \ge \frac{1}{2}.\) Phương pháp: Giải bất phương trình để tìm nghiệm. Lời giải: Đáp án đúng là: B Ta có: –2x + 1 < 0 –2x < –1
Bài 2.22 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Điều kiện xác định của phương trình \(\frac{x}{{2x + 1}} + \frac{3}{{x - 5}} = \frac{x}{{\left( {2x + 1} \right)\left( {x - 5} \right)}}\) là A. \(x \ne - \frac{1}{2}.\) B. \(x \ne - \frac{1}{2}\) và \(x \ne - 5.\) C. \(x \ne 5.\) D. \(x \ne - \frac{1}{2}\) và \(x \ne 5.\) Phương pháp: Điều kiện xác định của phương trình chứa ẩn ở mẫu là mẫu khác 0. Lời giải: Đáp án đúng là: D Ta có: (2x + 1)(x – 5) ≠ 0 khi 2x + 1 ≠ 0 và x – 5 ≠ 0. ⦁ 2x + 1 ≠ 0 khi 2x ≠ –1 hay x≠
⦁ x – 5 ≠ 0 khi x ≠ 5. Vậy điều kiện xác định của phương trình đã cho là x≠ Bài 2.23 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Phương trình \(x - 1 = m + 4\) có nghiệm lớn hơn 1 với A. \(m \ge - 4.\) B. \(m \le 4.\) C. \(m > - 4.\) D. \(m < - 4.\) Phương pháp: Giải phương trình để tìm x, vì phương trình có nghiệm lớn hơn 1 nên x > 1. Thay x để tìm giá trị của m. Lời giải: Đáp án đúng là: C Từ x – 1 = m + 4, suy ra x = m + 5. Theo bài, phương trình x – 1 = m + 4 có nghiệm lớn hơn 1 nên ta có: x > 1. Suy ra m + 5 >1, do đó m > –4. Bài 2.24 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Nghiệm của bất phương trình \(1 - 2x \ge 2 - x\) là A. \(x > \frac{1}{2}.\) B. \(x < \frac{1}{2}.\) C. \(x \le - 1.\) D. \(x \ge - 1.\) Phương pháp: Giải bất phương trình để tìm nghiệm. Lời giải: 1 – 2x ≥ 2 – x – 2x + x ≥ 2 – 1 –x ≥ 1 x ≤ –1. Vậy nghiệm của bất phương trình đã cho là x ≤ –1. Bài 2.25 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Cho \(a > b\) Khi đó ta có: A. \(2a > 3b.\) B. \(2a > 2b + 1.\) C. \(5a + 1 > 5b + 1.\) D. \( - 3a < - 3b - 3.\) Phương pháp: Áp dụng tính chất của bất đẳng thức: - Khi nhân cả hai vế của bất đẳng thức với một số dương ta được bất đẳng thức cùng chiều. - Khi nhân cả hai vế của bất đẳng thức với một số dương ta được bất đẳng thức ngược chiều. - Khi cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều. Lời giải: Đáp án đúng là: C Ta có: a > b, suy ra 5a > 5b, do đó 5a + 1 > 5b + 1. Vậy ta chọn phương án C. Bài 2.26 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Giải các phương trình sau: a) \({\left( {3x - 1} \right)^2} - {\left( {x + 2} \right)^2} = 0;\) b) \(x\left( {x + 1} \right) = 2\left( {{x^2} - 1} \right).\) Phương pháp: Đưa phương trình đã cho về dạng phương trình bậc nhất 1 ẩn \(ax + b = 0\left( {a \ne 0} \right)\) hoặc phương trình tích \(A\left( x \right).B\left( x \right) = 0\) (bằng cách phân tích đa thức thành nhân tử) Lời giải: a) (3x – 1)2 – (x + 2)2 = 0 (3x – 1 – x – 2)(3x – 1 + x + 2) = 0 (2x – 3)(4x + 1) = 0 2x – 3 = 0 hoặc 4x + 1 = 0 2x = 3 hoặc 4x = –1
b) x(x + 1) = 2(x2 – 1) x(x + 1) – 2(x2 – 1) = 0 x(x + 1) – 2(x + 1)(x – 1) = 0 (x + 1)(x – 2x + 2) = 0 (x + 1)(–x + 2) = 0 x + 1 = 0 hoặc –x + 2 = 0 x = –1 hoặc x = 2. Vậy phương trình đã cho có nghiệm là x = –1 hoặc x = 2. Bài 2.27 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Giải các phương trình sau: a) \(\frac{x}{{x - 5}} - \frac{2}{{x + 5}} = \frac{{{x^2}}}{{{x^2} - 25}};\) b) \(\frac{1}{{x - 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{3}{{{x^3} + 1}}.\) Phương pháp: Giải phương trình chứa ẩn ở mẫu: - Tìm ĐKXĐ - Quy đồng mẫu thức các phân thức và khử mẫu - Giải phương trình vừa nhận được và kết luận (đối chiếu điều kiện). Lời giải:
Suy ra x(x + 5) – 2(x – 5) = x2. (*) Giải phương trình (*): x(x + 5) – 2(x – 5) = x2 x2 + 5x – 2x + 10 – x2 = 0 3x = –10
Suy ra x2 – x + 1 – x(x + 1) = 3. (**) Giải phương trình (**): x2 – x + 1 – x(x + 1) = 3 x2 – x + 1 – x2 – x = 3 –2x = 2 x = – 1 (thỏa mãn điều kiện xác định). Vậy phương trình đã cho có nghiệm là x = –1. Bài 2.28 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Cho \(a < b,\) hãy so sánh: a) \(a + b + 5\) với \(2b + 5;\) b) \( - 2a - 3\) với \( - \left( {a + b} \right) - 3.\) Phương pháp: Áp dụng tính chất của bất đẳng thức: - Khi nhân cả hai vế của bất đẳng thức với một số dương ta được bất đẳng thức cùng chiều - Khi nhân cả hai vế của bất đẳng thức với một số dương ta được bất đẳng thức ngược chiều - Khi cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều Lời giải: a) Do a < b, nên a + b < b + b hay a + b < 2b. Suy ra a + b + 5 < 2b + 5. Vậy a + b + 5 < 2b + 5. b) Do a < b, nên a + a < a + b hay 2a < a + b. Suy ra –2a > –(a + b), do đó –2a – 3> – (a + b) – 3. Vậy –2a – 3 > – (a + b) – 3. Bài 2.29 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Giải các bất phương trình: a) \(2x + 3\left( {x + 1} \right) > 5x - \left( {2x - 4} \right);\) b) \(\left( {x + 1} \right)\left( {2x - 1} \right) < 2{x^2} - 4x + 1.\) Phương pháp: Đưa các phương trình đã cho về dạng bất phương trình bậc nhất 1 ẩn, bất phương trình bậc nhất một ẩn \(ax + b < 0\left( {a \ne 0} \right)\) được giải như sau: \(\begin{array}{l}ax + b < 0\\ax < - b.\end{array}\) Nếu \(a > 0\) thì \(x < \frac{{ - b}}{a}.\) Nếu \(a < 0\) thì \(x > \frac{{ - b}}{a}.\) Các bất phương trình \(ax + b > 0;ax + b \le 0;ax + b \ge 0\) giải tương tự. Lời giải: a) 2x + 3(x + 1) > 5x – (2x – 4) 2x + 3x + 3 > 5x – 2x + 4 5x + 3 > 3x + 4 5x – 3x > 4 – 3 2x > 1
b) (x + 1)(2x – 1) < 2x2 – 4x + 1 2x2 – x + 2x – 1 < 2x2 – 4x + 1 2x2 – x + 2x – 2x2 + 4x < 1 + 1 5x < 2
Bài 2.30 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức Một hãng viễn thông nước ngoài có hai gói cước như sau:
a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó. b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào? Phương pháp: a) Gọi thời gian gọi là x (phút) \(\left( {x > 0} \right)\) Biểu diễn số tiền phải trả khi gọi x phút đối với gói cước A, B. (Đối với gói cước A có 2 trường hợp: \(TH1:x \le 45\) \(TH2:x > 45\) Xác định phương trình cần tìm và giải. b) Ta cần tính số chi phí phải trả khi dùng cả hai gói cước, từ đó ta có lựa chọn gói cước cho phù hợp. Lời giải: a) Gọi x (phút) là thời gian gọi trong một tháng (x > 0). Theo bài, phí phải trả trong cùng một tháng của hai gói cước là như nhau, mà cước thuê bao hàng tháng của gói A nhỏ hơn gói B (32 < 44) nên thời gian gọi phải nhiều hơn 45 phút do tính thêm phí cho phút gọi thêm. Tức là x > 45. – Đối với gói cước A: ⦁ thời gian gọi thêm là: x – 45 (phút); ⦁ phí cần trả cho số phút gọi thêm là: 0,4.(x – 45) (USD); ⦁ phí phải trả cho hãng viễn thông là: T1 = 32 + 0,4.(x – 45) (USD). – Đối với gói cước B: ⦁ Phí cần trả cho x phút gọi là: 0,25x (USD); ⦁ Phí phải trả cho hãng viễn thông là: T2 = 44 + 0,25x (USD). Để phí phải trả trong cùng một tháng của hai gói cước là như nhau thì ta có phương trình sau: T1 = T2, hay 44 + 0,25x = 32 + 0,4.(x – 45). (*) Giải phương trình (*): 44 + 0,25x = 32 + 0,4.(x – 45) 44 + 0,25x = 32 + 0,4x – 0,4.45 0,25x – 0,4x = 32 – 18 – 44 –0,15x = –30 x = 200 (thỏa mãn điều kiện x > 45). Vậy thời gian gọi mà phí phải trả trong cùng một tháng của hai gói cước như nhau là 200 phút. b) – Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng, tức là x ≤ 180 thì: ⦁ x – 45 ≤ 180 – 45 hay x – 45 ≤ 135 Suy ra 0,4.(x – 45) ≤ 54 nên 32 + 0,4.(x – 45) ≤ 32 + 54 hay T1 ≤ 86. ⦁ 0,25x ≤ 45 nên 44 + 0,25x ≤ 44 + 45 hay T2 ≤ 89. Khi đó, khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước A để mất chi phí rẻ hơn. – Nếu khách hàng chỉ gọi tối đa là 500 phút trong 1 tháng, tức là x ≤ 500 thì: ⦁ x – 45 ≤ 500 – 45 hay x – 45 ≤ 455 Suy ra 0,4.(x – 45) ≤ 182 nên 32 + 0,4.(x – 45) ≤ 32 + 182 hay T1 ≤ 214. ⦁ 0,25x ≤ 125 nên 44 + 0,25x ≤ 44 + 125 hay T2 ≤ 169. Khi đó, khách hàng chỉ gọi tối đa là 500 phút trong 1 tháng thì nên dùng gói cước B để mất chi phí rẻ hơn. Bài 2.31 trang 43 SGK Toán 9 tập 1 - Kết nối tri thức Thanh tham dự một kì kiểm tra năng lực tiếng Anh gồm 4 bài kiểm tra nghe, nói, đọc và viết. Mỗi bài kiểm tra có điểm số nguyên từ 0 đến 10. Điểm trung bình của ba bài kiểm tra nghe, nói, đọc của Thanh là 6,7. Hỏi bài kiểm tra viết của Thanh cần được bao nhiêu điểm để điểm trung bình của cả 4 bài kiểm tra được từ 7,0 trở lên? Biết điểm trung bình được tính gần đúng đến chữ số thập phân thứ nhất. Phương pháp: Từ điểm trung bình, ta tính được tổng điểm các bài = điểm trung bình nhân với số bài, từ đó ta lập được bất phương trình biểu thị mối liên hệ giữa các ẩn. Lời giải: Tổng điểm của ba môn nghe, nói, đọc của Thanh khoảng: 6,7 . 3 = 20,1 ≈ 20 (do mỗi bài kiểm tra có điểm là số nguyên từ 0 đến 10). Gọi x là điểm bài kiểm tra viết của Thanh (0 < x ≤ 10, x ∈ ℕ*). Khi đó điểm trung bình bốn bài kiểm tra của Thanh là: Để điểm trung bình cả 4 bài kiểm tra được từ 7,0 trở lên thì: 20 + x ≥ 28 x ≥ 8. Mà 0 < x ≤ 10, x ∈ ℕ* nên x ∈ {8; 9; 10}. Vậy bài kiểm tra viết của Thanh cần được 8 điểm hoặc 9 điểm hoặc 10 điểm để điểm trung bình cả 4 bài kiểm tra được từ 7,0 trở lên. Bài 2.32 trang 43 SGK Toán 9 tập 1 - Kết nối tri thức Để lập đội tuyển năng khiếu về bóng rổ của trường, thầy thể dục đưa ra quy định tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 15 quả bóng vào rổ, quả bóng vào rổ được cộng 2 điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào đội tuyển. Hỏi một học sinh muốn được chọn vào đội tuyển thì phải ném ít nhất bao nhiêu quả vào rổ? Phương pháp: Số điểm học sinh đạt được khi ném 15 quả bóng = số điểm ném trúng (số lần ném trúng nhân 2) – số điểm ném trượt (số quả trượt nhân 1) Và số điểm tối thiểu để vào đội tuyển cần 15 điểm, từ đó ta lập được bất phương trình. Lời giải: Gọi x là số quả bóng học sinh cần ném vào rổ (0 ≤ x ≤ 15, x ∈ ℕ*). Số quả bóng ném ra ngoài là: 15 – x (quả). Ném vào rổ x quả bóng được cộng 2x (điểm). Ném ra ngoài 15 – x quả bóng bị trừ 15 – x (điểm). Vì vậy, sau khi ném 15 quả bóng thì học sinh đó sẽ có số điểm là: 2x – (15 – x) = 2x – 15 + x = 3x – 15 (điểm). Theo bài, để được vào đội tuyển thì học sinh cần có số điểm từ 15 trở lên, nên ta có bất phương trình: 3x – 15 ≥ 15 3x ≥ 30 x ≥ 10. Mà 0 ≤ x ≤ 15, x ∈ ℕ* nên học sinh đó cần phải ném vào rổ ít nhất là 10 quả bóng thì mới được chọn vào đội tuyển. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 2
|

 Tải ngay
Tải ngay
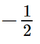

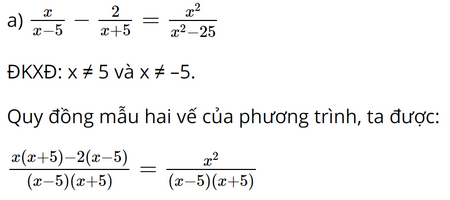




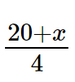
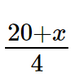 ≥ 7,0
≥ 7,0