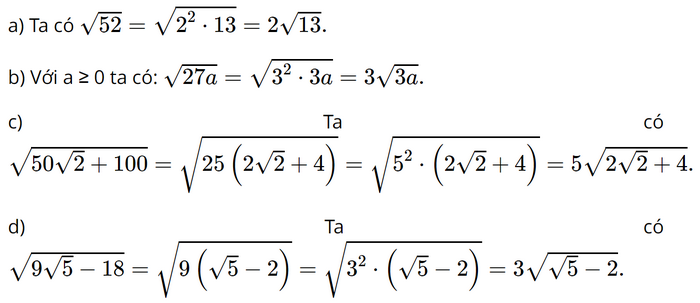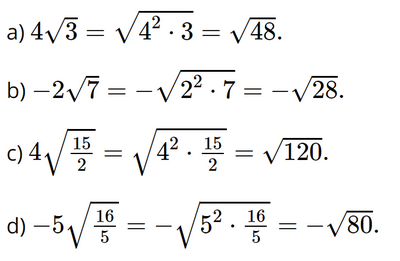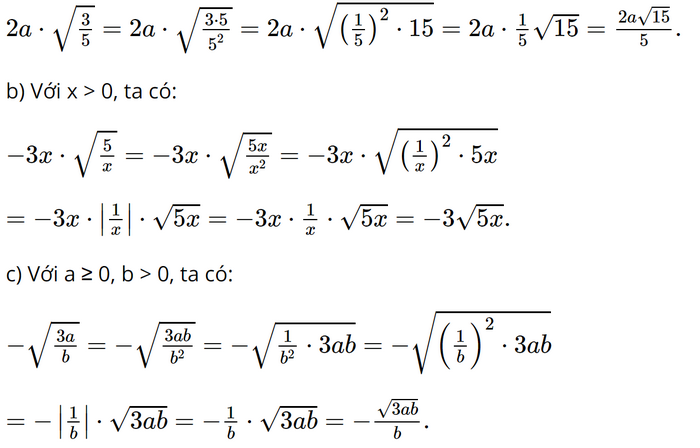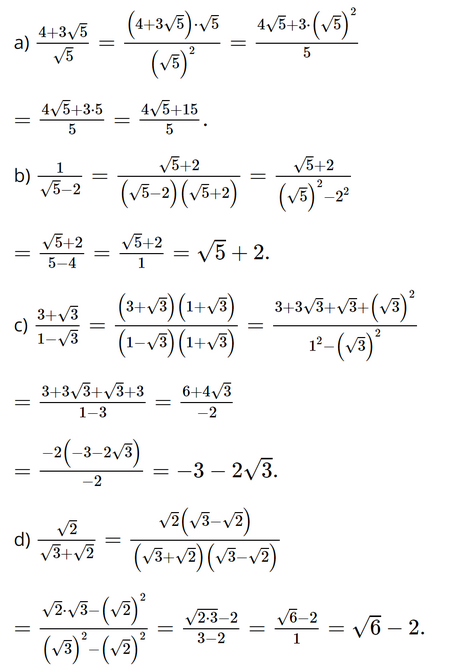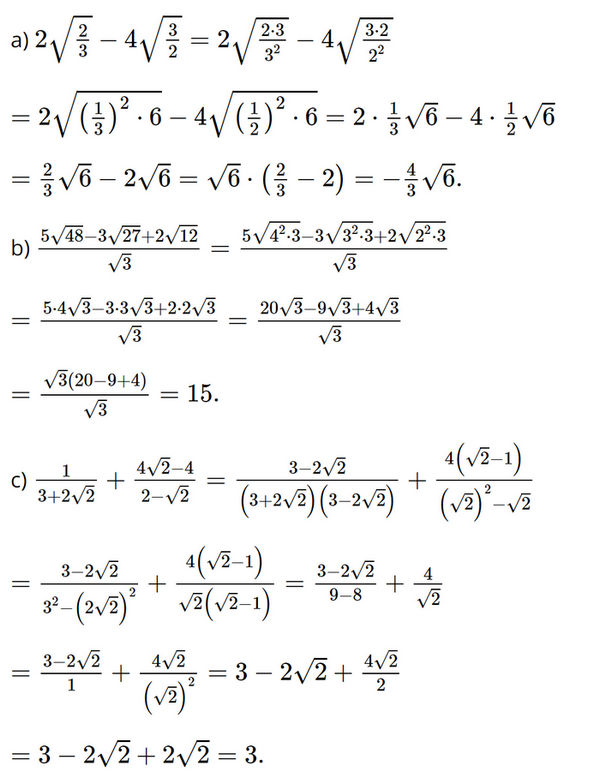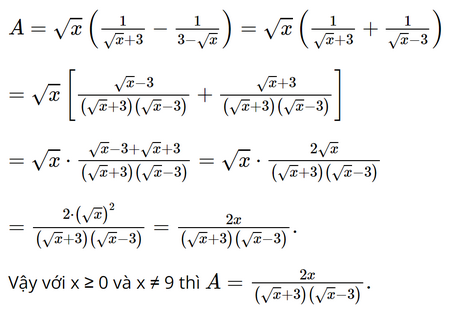Giải bài 3.17, 3.18, 3.19, 3.20, 3.21, 3.22 trang 59 SGK Toán 9 Kết nối tri thức tập 1

Bài 3.17 trang 59 SGK Toán 9 tập 1 - Kết nối tri thức

Đưa thừa số ra ngoài dấu căn:

a) \(\sqrt {75} ;\)

b) \(\sqrt {27a} \left( {a \ge 0} \right);\)

c) \(\sqrt {50\sqrt 2  + 100} ;\)

d) \(\sqrt {9\sqrt 5  - 18} .\)

Phương pháp:

Ta có \(\sqrt {{A^2}B}  = \left| A \right|.\sqrt B \)

Lời giải:

Bài 3.18 trang 59 SGK Toán 9 tập 1 - Kết nối tri thức

Đưa thừa số vào trong dấu căn:

a) \(3\sqrt 2 ;\)

b) \( - 2\sqrt 7 ;\)

c) \(4\sqrt {\frac{{15}}{2}} ;\)

d) \( - 5\sqrt {\frac{{16}}{5}} .\)

Phương pháp:

Ta có: \(a\sqrt b  = \sqrt {{a^2}b} \) khi \(a,b > 0.\)

\(a\sqrt b  =  - \sqrt {{a^2}b} \) khi \(a < 0,b > 0.\)

Lời giải:

Bài 3.19 trang 59 SGK Toán 9 tập 1 - Kết nối tri thức

Khử mẫu trong dấu căn:

a) \(2a.\sqrt {\frac{3}{5}} ;\)

b) \( - 3x.\sqrt {\frac{5}{x}} \left( {x > 0} \right);\)

c) \( - \sqrt {\frac{{3a}}{b}} \left( {a \ge 0,b > 0} \right).\)

Phương pháp:

Ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\)

Lời giải:

a) Ta có:

Bài 3.20 trang 59 SGK Toán 9 tập 1 - Kết nối tri thức

Trục căn thức ở mẫu:

a) \(\frac{{4 + 3\sqrt 5 }}{{\sqrt 5 }};\)

b) \(\frac{1}{{\sqrt 5  - 2}};\)

c) \(\frac{{3 + \sqrt 3 }}{{1 - \sqrt 3 }};\)

d) \(\frac{{\sqrt 2 }}{{\sqrt 3  + \sqrt 2 }}.\)

Phương pháp:

Ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\); \(\frac{C}{{\sqrt A  + \sqrt B }} = \frac{{C\left( {\sqrt A  - \sqrt B } \right)}}{{A - B}}\); \(\frac{C}{{\sqrt A  - B}} = \frac{{C\left( {\sqrt A  + B} \right)}}{{\left( {\sqrt A  - B} \right)\left( {\sqrt A  + B} \right)}}\);\(\frac{C}{{A - \sqrt B }} = \frac{{C\left( {A - \sqrt B } \right)}}{{\left( {A - \sqrt B } \right)\left( {A + \sqrt B } \right)}}\)

Chú ý nếu biểu thức rút gọn được thì ta rút gọn trước khi trục căn thức.

Lời giải:

Bài 3.21 trang 59 SGK Toán 9 tập 1 - Kết nối tri thức

Rút gọn các biểu thức sau:

a) \(2\sqrt {\frac{2}{3}}  - 4\sqrt {\frac{3}{2}} ;\)

b) \(\frac{{5\sqrt {48}  - 3\sqrt {27}  + 2\sqrt {12} }}{{\sqrt 3 }};\)

c) \(\frac{1}{{3 + 2\sqrt 2 }} + \frac{{4\sqrt 2  - 4}}{{2 - \sqrt 2 }}.\)

Phương pháp:

Sử dụng trục căn thức để khử mẫu, đưa thừa số ra ngoài dấu căn và đưa vào trong dấu căn, kết hợp các phương pháp để rút gọn biểu thức

Lời giải:

Bài 3.22 trang 59 SGK Toán 9 tập 1 - Kết nối tri thức

Rút gọn biểu thức \(A = \sqrt x \left( {\frac{1}{{\sqrt x  + 3}} - \frac{1}{{3 - \sqrt x }}} \right)\left( {x \ge 0,x \ne 9} \right).\)

Phương pháp:

Đối với biểu thức trên ta có thể sử dụng trục căn thức ở mẫu. Rồi quy đồng mẫu rồi cộng trừ như cộng trừ phân thức.

Lời giải:

Với x ≥ 0 và x ≠ 9, ta có:

Sachbaitap.com