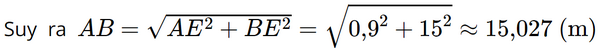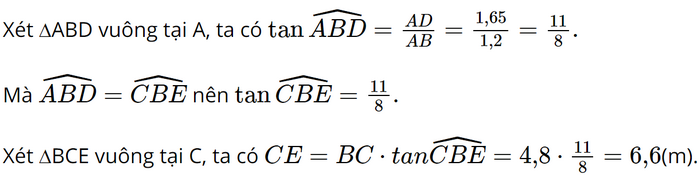Giải bài 4.8, 4.9, 4.10, 4.11, 4.12, 4.13 trang 78 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 78 Kết nối tri thức tập 1.Bài 4.11: Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và (sqrt 3 .) Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69) . Bài 4.8 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức Giải tam giác ABC vuông tại A có \(BC = a,AC = b,AB = c,\) trong các trường hợp: a) \(a = 21,b = 18;\) b) \(b = 10,\widehat C = {30^0};\) c) \(c = 5,b = 3.\) Phương pháp: Dựa vào tỉ số lượng giác giữa các cạnh ta tính được góc B hoặc góc C, và các biểu thức liên quan giữa cạnh và góc chưa biết kết hợp thêm định lý Pythagore để tính cạnh còn lại khi biết hai cạnh. Lời giải:
a) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a2 = b2 + c2
Vậy ∆ABC có
Bài 4.9 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức Tính góc nghiêng \(\alpha \) của thùng xe chở rác trong Hình 4.22
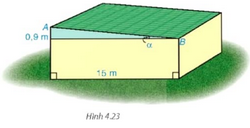
Phương pháp: Sử dụng tỉ số lượng giác liên quan đến cạnh kề và cạnh huyền trong tam giác vuông (\(\cos \alpha \)) Lời giải: Theo định nghĩa tỉ số lượng giác cos, ta có Vậy góc nghiêng α của thùng xe chở rác khoảng 36°52’. Bài 4.10 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức Tính góc nghiêng \(\alpha \) và chiều rộng AB của mái nhà kho trong Hình 4.23
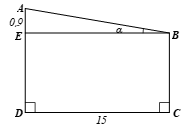
Phương pháp: Để tính góc cần lập tỉ số lượng giác liên quan giữa cạnh đối và cạnh kề của tam giác vuông (\(\tan \alpha \)). Để tính cạnh AB ta có thể sử dụng định lý Pythagore. Lời giải: Theo đề ta có hình vẽ:
Tứ giác BCDE là hình chữ nhật nên BE = CD = 15 m. Xét ∆ABE vuông tại E, theo định nghĩa tỉ số lượng giác tan, ta có:
Theo định lí Pythagore, ta có: AB2 = AE2 + BE2.
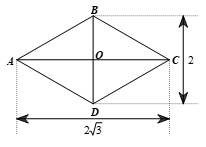
Vậy góc nghiêng của mái nhà kho khoảng 3°26’ và chiều rộng của mái nhà kho khoảng 15,027 m. Bài 4.11 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt 3 .\) Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69) . Phương pháp: Góc giữa cạnh ngắn hơn và đường chéo của hình chữ nhật chính là góc nhọn trong tam giác vuông khi biết cạnh đối và cạnh kề, ta sử dụng tỉ số lượng giác \(\tan ,\cot \) Lời giải: Theo đề ta có hình vẽ:
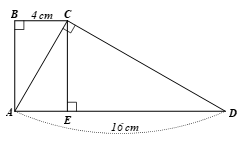
Bài 4.12 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức Cho hình thang ABCD (AD // BC) có \(AD = 16cm,BC = 4cm,\widehat A = \widehat B = \widehat {ACD} = {90^0}.\) a) Kẻ đường cao CE của tam giác ACD. Chứng minh \(\widehat {ADC} = \widehat {ACE}.\) Tính sin của các góc \(\widehat {ADC},\widehat {ACE}\) và suy ra \(A{C^2} = AE.AD.\) Từ đó tính AC. b) Tính góc D của hình thang. Phương pháp: Từ hai góc bằng nhau nên ta có tỉ số lượng giác của hai góc gần như nhau. Từ đó ta lập được tỉ lệ của hai góc này. Rồi tính AC, góc D. Lời giải:
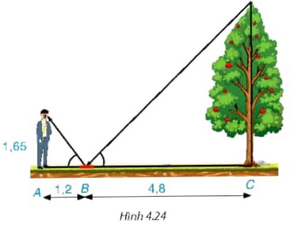
Bài 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).
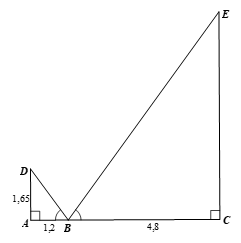
Phương pháp: Góc tạo bởi đoạn thẳng nối từ mắt người đứng tới gương và đoạn thẳng AB bằng góc tạo bởi đoạn thẳng nối từ ngọn cây đến gương và đoạn thẳng BC. Từ đó ta có thể sử dụng tam giác đồng dạng theo trường hợp góc góc để suy ra tỉ lệ các cạnh tương ứng, từ đó ta giải ra được chiều cao của cây, hoặc sử dụng tỉ số lượng giác của hai góc trên (\(\tan \alpha \) ) để tính chiều cao của cây. Tuy nhiên đối với cot thì ta có thể làm như sau: \(\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}}\) hoặc sử dụng tính chất hai góc phụ nhau có tan bằng cot. Lời giải: Theo đề ta có hình vẽ:
Vậy chiều cao của cây là 6,6 m. Sachbaitap.com
Xem thêm tại đây:
Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
|
-

Giải bài 4.14, 4.15, 4.16, 4.17, 4.18, 4.19, 4.20 trang 81 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 81 Kết nối tri thức tập 1.Bài 4.14: Một cuốn sách khổ (17 times 24) cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi (alpha) là góc giữa đường chéo và cạnh 17 cm. Tính (sin alpha ,cos alpha) (làm tròn đến chữ số thập phân thứ hai) và tính số đo (alpha) (làm tròn đến độ) .

 Tải ngay
Tải ngay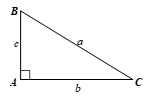
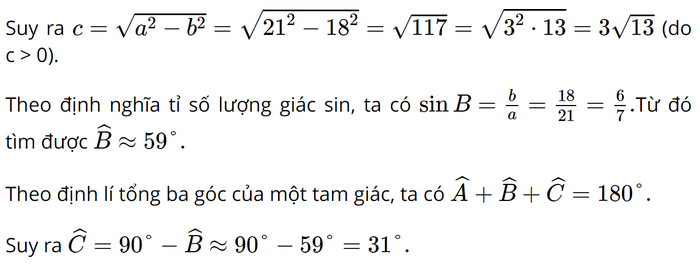
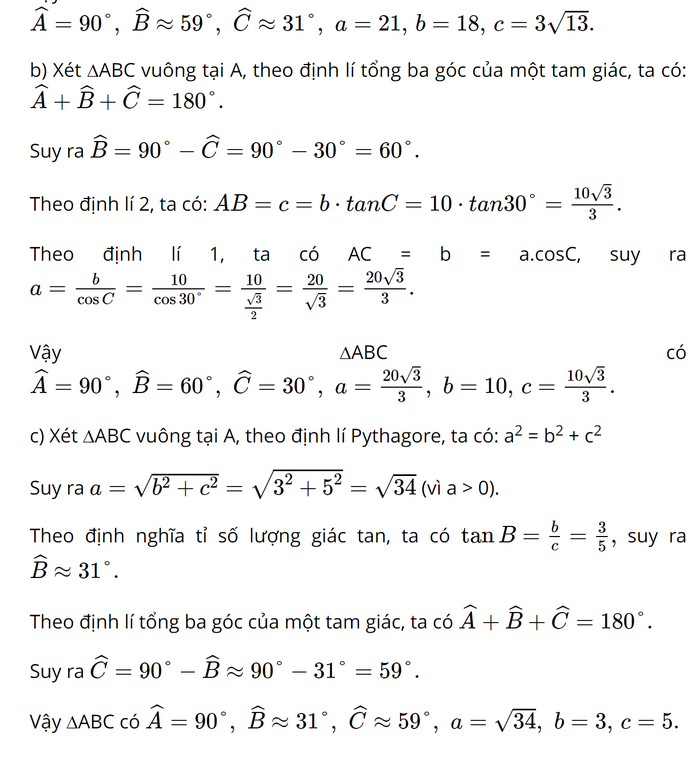
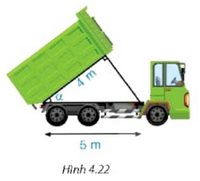
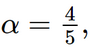 từ đó tính được α ≈ 36°52’.
từ đó tính được α ≈ 36°52’.