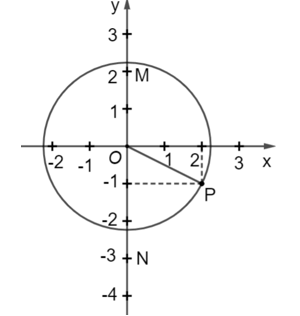
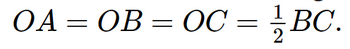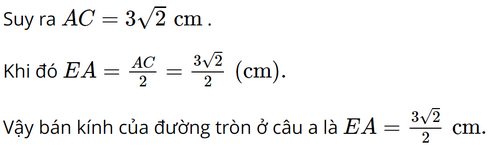Giải bài 5.1, 5.2, 5.3, 5.4 trang 86 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 86 Kết nối tri thức tập 1.Bài 5.2: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó. Bài 5.3: Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O. a) Ba điểm B, C và D có thuộc (O) hay không? Vì sao? Bài 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức Trong mặt phẳng tọa độ Oxy, cho các điểm M (0 ; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\)? Vì sao? Phương pháp: Vẽ đường tròn \(\left( {O;\sqrt 5 } \right)\) và các điểm M (0; 2), N (0; -3) và P(2; -1). Sau đó dựa vào hình vẽ xác định điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\). Lời giải:
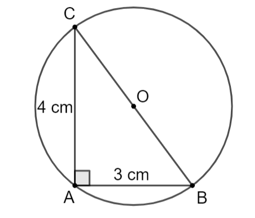
Bài 5.2 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó. Phương pháp: - Từ định lý Pythagore tính được độ dài cạnh BC. - Từ tính chất đường trung tuyến trong tam giác vuông suy ra A, B, C thuộc đường tròn đường kính BC. Lời giải:
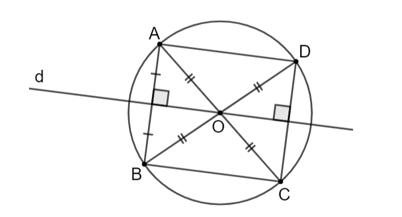
Gọi O là trung điểm của BC. Ta có AO là trung tuyến ứng với cạnh huyền nên Suy ra A, B, C cùng thuộc đường tròn bán kính OA. Tâm O là trung điểm của BC nên BC là đường kính. Do đó, các điểm A, B, C thuộc cùng một đường tròn. Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có: BC2 = AB2 + AC2 = 32 + 42 = 25. Suy ra BC = 5 cm. Khi đó OA = 1/2 BC = 5/2 = 2,5 (cm) Vậy các điểm A, B, C thuộc cùng một đường tròn và có bán kính là 2,5 cm. Bài 5.3 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O. a) Ba điểm B, C và D có thuộc (O) hay không? Vì sao? b) Chứng minh tứ giác ABCD là hình chữ nhật. c) Chứng minh rằng C và D đối xứng với nhau qua d. Phương pháp: Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng, ở đây d là trục đối xứng của đường tròn tâm O, nên B đối xứng với A qua d thì B thuộc đường tròn Đường tròn là hình có tâm đối xứng, tâm đối xứng chính là tâm của hình tròn, B và A thuộc đường tròn nên C và D cũng thuộc đường tròn. ABCD là hình chữ nhật dựa vào dấu hiệu hình bình hành có hai đường chéo bằng nhau. C và D đối xứng với nhau qua d khi d là trung trực của CD. Lời giải:
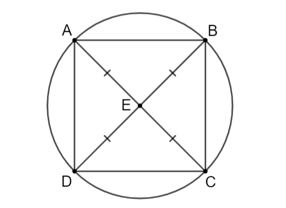
a) Ta có d là là đường thẳng đi qua tâm O nên d là trục đối xứng của đường tròn. Vì A thuộc (O) và B là điểm đối xứng của A qua d nên B cũng thuộc (O). Vì C, D lần lượt là điểm đối xứng của A, B qua O nên C, D cũng thuộc (O). b) C đối xứng với A qua O nên O là trung điểm của AC. D đối xứng với B qua O nên O là trung điểm của BD. Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường. Mà BD = CD (bằng 2 lần bán kính (O)). Do đó, tứ giác ABCD là hình chữ nhật. c) Vì ABCD là hình chữ nhật nên AB // CD, mà AB ⊥ d nên d ⊥ CD. Xét tam giác OCD có OC = OD nên tam giác OCD cân tại O. Mà đường thẳng d là đường cao của tam giác OCD nên d cũng là trung trực của CD. Hay C và D đối xứng nhau qua đường thẳng d. Bài 5.4 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức Cho hình vuông ABCD có E là giao điểm của hai đường chéo. a) Chứng minh rằng chỉ có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó. b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3 cm. Phương pháp: a) Sử dụng tính chất 2 đường chéo của hình vuông, từ đó suy ra bốn điểm A, B, C, D cùng thuộc (O). b) Sử dụng định lý Pythagore ta tính độ dài đường chéo của hình vuông và chính là đường kính của đường tròn, từ đó ta tính được bán kính. Lời giải:
a) Do ABCD là hình vuông nên AC = BD và E là trung điểm của AC và BD. Suy ra: EA = EB = EC = ED. Do đó các điểm A, B, C, D cùng thuộc một đường tròn hay chỉ có một đường tròn duy nhất đi qua bốn điểm này. Đường tròn (E) có tâm E là tâm đối xứng và có hai trục đối xứng là AC và BD. b) Hình vuông có cạnh bằng 3 cm nên AB = BC = CD = DA = 3 cm. Áp dụng định lý Pythagore vào tam giác ABC vuông tại B, ta có: AC2 = AB2 + BC2 = 32 + 32 = 18. Sachbaitap.com
Xem thêm tại đây:
Bài 13: Mở đầu về đường tròn
|
-

Giải bài 5.5, 5.6, 5.7, 5.8 trang 90 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 90 Kết nối tri thức tập 1.Bài 5.7: Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng (100^circ )(làm tròn kết quả đến hàng phần mười).

 Tải ngay
Tải ngay