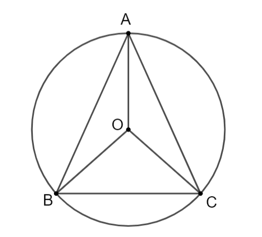
Giải bài 5.9, 5.10, 5.11, 5.12, 5.13 trang 95 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 95 Kết nối tri thức tập 1.Bài 5.12 Có hai chiếc bánh pizza hình tròn (H.5.18). Chiếc bánh thứ nhất có đường kính 16 cm được cắt thành 6 miếng đều nhau có dạng hình quạt tròn. Chiếc bánh thứ hai có đường kính 18 cm được cắt thành 8 miếng đều nhau có dạng hình quạt tròn. Hãy so sánh diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất và thứ hai. Bài 5.9 trang 94 SGK Toán 9 tập 1 - Kết nối tri thức Cho đường tròn (O; 4 cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng \(70^\circ .\) a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau. b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười). Phương pháp: a) Xét \(\Delta OAB\) và \(\Delta OAC\) từ đó suy ra\(\widehat {AOB} = \widehat {AOC}\) b) Tính số đo cung AB và AC, sau đó áp dụng công thức tính độ dài cung. Lời giải:
a) Xét ΔOAB và ΔOAC có: Cạnh OA chung OA = OC = R AB = AC (do ΔABC cân tại A). Do đó ΔOAB = ΔOAC (c.c.c).
Bài 5.10 trang 95 SGK Toán 9 tập 1 - Kết nối tri thức Tính diện tích của hình quạt tròn bán kính 4 cm, ứng với cung \(36^\circ .\) Phương pháp: Áp dụng công thức tính diện tích hình quạt tròn ứng với của cung \(n^\circ \): \({\rm{S = }}\frac{{\rm{n}}}{{{\rm{360}}}}{\rm{.\pi }}{{\rm{R}}^2}\) Lời giải: Diện tích của hình quạt tròn bán kính 4 cm, ứng với cung 36° là: 36/360 . π . 42 = 1,6π (cm2) Vậy diện tích của hình quạt tròn bán kính 4 cm, ứng với cung 36° là 1,6π cm2. Bài 5.11 trang 95 SGK Toán 9 tập 1 - Kết nối tri thức Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 cm và 4 cm. Phương pháp: Áp dụng công thức tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r) là: \(\pi \left( {{R^2} - {r^2}} \right).\) Lời giải: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 cm và 4 cm là: π(52 − 42) = 9π (cm2). Vậy diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 cm và 4 cm là 9π cm2. Bài 5.12 trang 95 SGK Toán 9 tập 1 - Kết nối tri thức Có hai chiếc bánh pizza hình tròn (H.5.18). Chiếc bánh thứ nhất có đường kính 16 cm được cắt thành 6 miếng đều nhau có dạng hình quạt tròn. Chiếc bánh thứ hai có đường kính 18 cm được cắt thành 8 miếng đều nhau có dạng hình quạt tròn. Hãy so sánh diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất và thứ hai.
Phương pháp: Lần lượt tính diện tích của mỗi miếng bánh = Diện tích hìnhh tròn : Số miếng Sau đó so sánh diện tích hai miếng bánh. Lời giải: Diện tích bề mặt của mỗi miếng bánh cắt ra từ chiếc bánh thứ nhất là
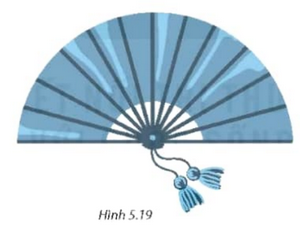
Vậy diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất lớn hơn chiếc bánh thứ hai. Bài 5.13 trang 95 SGK Toán 9 tập 1 - Kết nối tri thức Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 2,2 dm như hình 5.19. Tính diện tích phần giấy của chiếc quạt, biết rằng khi gấp lại, phần giấy có chiều dài khoảng 1,6 dm (làm tròn kết quả đến hàng trăm của dm2).
Phương pháp: Diện tích phần giấy của chiếc quạt là diện tích của hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính 2,2 dm và 1,6 dm. Áp dụng công thức tính diện tích hình vành khuyên: \(\pi \left( {{R^2} - {r^2}} \right).\) Lời giải: Diện tích phần giấy của chiếc quạt là: π(2,22 − 1,62) = 2,28π (dm2). Vậy diện tích phần giấy của chiếc quạt là 2,28π (dm2). Sachbaitap.com
|
-

Giải bài 5.14, 5.15, 5.16, 5.17, 5.18, 5.19 trang 96 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 96 Kết nối tri thức tập 1. Bài 5.15: Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng: a) Đường tròn đường kính BC đi qua các điểm H và K;b) KH < BC.

 Tải ngay
Tải ngay