Giải bài 6.36, 6.37, 6.38, 6.39, 6.40, 6.41, 6.42, 6.43, 6.44 trang 25, 26 SGK Toán 8 Kết nối tri thức tập 2Giải sách giáo khoa Toán lớp 8 trang 25,26 Kết nối tri thức với cuộc sống tập 2: bài 6.36, 6.37, 6.38, 6.39, 6.40, 6.41, 6.42, 6.43, 6.44. Một xe ô tô đi từ Hà Nội đến Vinh với vận tốc 60km/h và dự kiến sẽ đến Vinh sau 5 giờ chạy. Tuy nhiên, sau 2/3 giờ chạy với vận tốc 60km/h, xe dừng nghỉ 20 phút. Sau khi dừng nghỉ, để đến Vinh đúng thời gian dự kiến, xe phải tăng vận tốc so với chặng đầu. Bài 6.36 trang 25 SGK Toán 8 tập 2 - Kết nối tri thức Khẳng định nào sau đây là đúng: A. \(\frac{{{{\left( {x - 1} \right)}^2}}}{{x - 2}} = \frac{{{{\left( {1 - x} \right)}^2}}}{{2 - x}}\) B. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{\rm{x}}}}{{{{\left( {x - 2} \right)}^2}}}\) C. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - 3{\rm{x}}}}{{{{\left( {x - 2} \right)}^2}}}\) D. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{\rm{x}}}}{{{{\left( { - x - 2} \right)}^2}}}\)\(\) Phương pháp: Ta thấy \({\left( {x + 2} \right)^2} = {\left( { - x - 2} \right)^2}\) để tìm ra được đáp án đúng Lời giải: Đáp án đúng là: D Khẳng định D là đúng vì (x + 2)2 = (–x – 2)2. Bài 6.37 trang 25 SGK Toán 8 tập 2 - Kết nối tri thức Khẳng định nào sau đây là sai: A. \(\frac{{ - 6{\rm{x}}}}{{ - 4{{\rm{x}}^2}{{\left( {x + 2} \right)}^2}}} = \frac{3}{{2{\rm{x}}{{\left( {x + 2} \right)}^2}}}\) B. \(\frac{{ - 5}}{{ - 2}} = \frac{{10{\rm{x}}}}{{4{\rm{x}}}}\) C. \(\frac{{x + 1}}{{x - 1}} = \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}}\) D. \(\frac{{ - 6{\rm{x}}}}{{ - 4{{\left( { - x} \right)}^2}{{\left( {x - 2} \right)}^2}}} = \frac{3}{{2{\rm{x}}{{\left( { - x + 2} \right)}^2}}}\) Phương pháp: Xem xét các đáp án tìm ra đáp án vô lí là khẳng định sai Lời giải: Đáp án đúng là: C Khẳng định C là sai vì: (x + 1)(x2 – x + 1) = x3 + 1 và (x – 1)(x2 + x + 1) = x3 – 1. Suy ra (x + 1)(x2 – x + 1) ≠ (x – 1)(x2 + x + 1). Do đó, Bài 6.38 trang 25 SGK Toán 8 tập 2 - Kết nối tri thức Trong hằng đẳng thức \(\frac{{2{{\rm{x}}^2} + 1}}{{4{\rm{x}} - 1}} = \frac{{8{{\rm{x}}^3} + 4{\rm{x}}}}{Q}\), Q là đa thức A.4x B. \(4{{\rm{x}}^2}\) C.16x−4 D. \(16{{\rm{x}}^2} - 4{\rm{x}}\) Phương pháp: Áp dụng hai phân thức bằng nhau để tìm Q. Lời giải: Đáp án đúng là: D
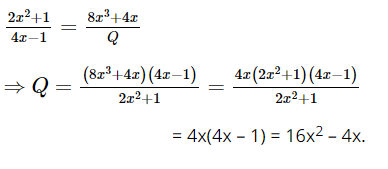 Bài 6.39 trang 25 SGK Toán Kết nối tri thức
Nếu \(\frac{{ - 5{\rm{x}} + 5}}{{2{\rm{x}}y}} - \frac{{ - 9{\rm{x}} - 7}}{{2{\rm{x}}y}} = \frac{{b{\rm{x}} + c}}{{xy}}\) thì b + c
A. -4 B. 8 C. 4 D. -10 Phương pháp: Ta rút gọn \(\frac{{ - 5{\rm{x}} + 5}}{{2{\rm{x}}y}} - \frac{{ - 9{\rm{x}} - 7}}{{2{\rm{x}}y}} \) rồi tính b + c Lời giải: Đáp án đúng là: B Ta có: Suy ra b = 2 và c = 6. Vậy b + c = 2 + 6 = 8 Bài 6.40 trang 25 SGK Toán 8 tập 2 - Kết nối tri thức Một ngân hàng huy động vốn với mức lãi suất một năm là x%. Để sau một năm, người gửi lãi a đồng thì người đó phải gửi vào ngân hàng số tiền là: A. \(\frac{{100{\rm{a}}}}{x}\) (đồng) B. \(\frac{a}{{x + 100}}\) (đồng) C. \(\frac{a}{{x + 1}}\) (đồng) D. \(\frac{{100{\rm{a}}}}{{x + 100}}\) (đồng) Phương pháp: Tính số tiền người đó gửi vào ngân hàng rồi đưa ra phương án lựa chọn Lời giải: Đáp án đúng là: A Sau một năm, người gửi lãi a đồng thì người đó phải gửi vào ngân hàng số tiền là:
Vì Bài 6.41 trang 26 SGK Toán 8 tập 2 - Kết nối tri thức Tìm đa thức P trong các đẳng thức sau: a) \(P + \frac{1}{{x + 2}} = \frac{x}{{{x^2} - 2{\rm{x}} + 4}}\) b) \(P - \frac{{4\left( {x - 2} \right)}}{{x + 2}} = \frac{{16}}{{x - 2}}\) c) \(P.\frac{{x - 2}}{{x + 3}} = \frac{{{x^2} - 4{\rm{x}} + 4}}{{{x^2} - 9}}\) d) \(P:\frac{{{x^2} - 9}}{{2{\rm{x}} + 4}} = \frac{{{x^2} - 4}}{{{x^2} + 3{\rm{x}}}}\) Phương pháp: Áp dụng quy tắc chuyển vế trong từng bài toán Lời giải:
Bài 6.42 trang 26 SGK Toán 8 tập 2 - Kết nối tri thức Rút gọn biểu thức sau: a) \(\frac{2}{{3{\rm{x}}}} + \frac{x}{{x - 1}} + \frac{{6{{\rm{x}}^2} - 4}}{{2{\rm{x}}\left( {1 - x} \right)}}\) b) \(\frac{{{x^3} + 1}}{{1 - {x^3}}} + \frac{x}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}\) c) \(\left( {\frac{2}{{x + 2}} - \frac{2}{{1 - x}}} \right).\frac{{{x^2} - 4}}{{4{{\rm{x}}^2} - 1}}\) d) \(1 + \frac{{{x^3} - x}}{{{x^2} + 1}}\left( {\frac{1}{{1 - x}} - \frac{1}{{1 - {x^2}}}} \right)\) Phương pháp: Thực hiện theo quy tắc cộng, trừ, nhân, chia các phân thức đại số Lời giải:
Bài 6.43 trang 26 SGK Toán 8 tập 2 - Kết nối tri thức Cho phân thức: \(P = \frac{{2{\rm{x}} + 1}}{{x + 1}}\) a) Viết điều kiện xác định của P b) Hãy viết P dưới dạng \(a - \frac{b}{{x + 1}}\), trong đó a, b là số nguyên dương c) Với giá trị nào của x thì P có giá trị là số nguyên Phương pháp: Điều kiện xác định của P là \(x + 1 \ne 0\) Ta tách: \(P = \frac{{2{\rm{x}} + 1}}{{x + 1}} = \frac{{2{\rm{x}} + 2 - 1}}{{x + 1}} = 2 - \frac{1}{{x + 1}}\) từ đó xác định được a, b Để P nguyên thì \(\frac{1}{{x + 1}}\) nguyên Lời giải: a) Điều kiện xác định của P là x + 1 ≠ 0 hay x ≠ –1. b) c) Vì Do vậy x + 1 = – 1, suy ra x = – 2 hoặc x + 1 = 1, suy ra x = 0. Vậy giá trị của P là số nguyên khi x = 0 hoặc x = – 2. Bài 6.43 trang 26 SGK Toán 8 tập 2 - Kết nối tri thức Một xe ô tô đi từ Hà Nội đến Vinh với vận tốc 60km/h và dự kiến sẽ đến Vinh sau 5 giờ chạy. Tuy nhiên, sau \(2\frac{2}{3}\) giờ chạy với vận tốc 60km/h, xe dừng nghỉ 20 phút. Sau khi dừng nghỉ, để đến Vinh đúng thời gian dự kiến, xe phải tăng vận tốc so với chặng đầu a) Tính độ dài quãng đường Hà Nội - Vinh b) Tính độ dài quãng đường còn lại sau khi dừng nghỉ c) Cho biết ở chặng thứ hai xe tăng vận tốc thêm x (km/h). Hãy viết biểu thức P biểu thị thời gian (tính bằng giờ) thực tế xe chạy hết chặng đường Hà Nội - Vinh d) Tính thời gian của P lần lượt tại x = 5, x = 10; x = 15, từ đó cho biết ở chặng thứ hai (sau khi xe dừng nghỉ): - Nếu tăng vận tốc thêm 5km/h thì xe đến Vinh muộn hơn dự kiến bao nhiêu giờ? - Nếu tăng vận tốc thêm 10km/h thì xe đến Vinh có đúng thời gian dự kiến không? - Nếu tăng vận tốc thêm 15km/h thì xe đến Vinh sớm hơn dự kiến bao nhiêu giờ? Phương pháp: Dựa vào thời gian và vận tốc đề bài cho để tính quãng đường Hà Nội – Vinh và quãng đường còn lại sau khi dừng. Viết biểu thức P biểu thị thời gian (tính bằng giờ) thực tế xe chạy hết chặng đường Hà Nội - Vinh Thay các giá trị x đã cho x = 5; x = 10; x = 15 để tính thời gia thực tế xe chạy chằng đường Hà Nội - Vinh Lời giải: a) Quãng đường Hà Nội – Vinh dài 5.60 = 300 (km). b) Trước khi dừng nghỉ, xe chạy trong Chiều dài chặng đầu là Chặng còn lại dài 300 – 160 = 140 (km). c) Nếu vận tốc tăng thêm x (km/h) thì vận tốc thực tế của xe chạy trên chặng sau là 60 + x (km/h). Thời gian thực tế xe chạy chặng sau là Thời gian xe chạy chặng đầu là Vì vậy thực tế xe chạy từ Hà Nội đến Vinh trong thời gian là:
d) Giá trị của
– Nếu tăng vận tốc thêm 5 km/h (tức là x = 5) thì thời gian chạy Hà Nội đến Vinh là – Nếu tăng vận tốc thêm 10 km/h (tức là x = 10) thì thời gian chạy Hà Nội đến Vinh là 5 giờ nên xe đến Vinh đúng thời gian dự định. – Nếu tăng vận tốc thêm 15 km/h (tức là x = 15) thì thời gian chạy Hà Nội đến Vinh là Sachbaitap.com
Xem thêm tại đây:
Luyện tập chung (trang 23)
|

 Tải ngay
Tải ngay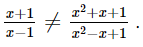
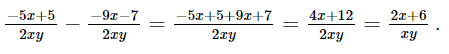
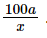
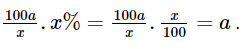

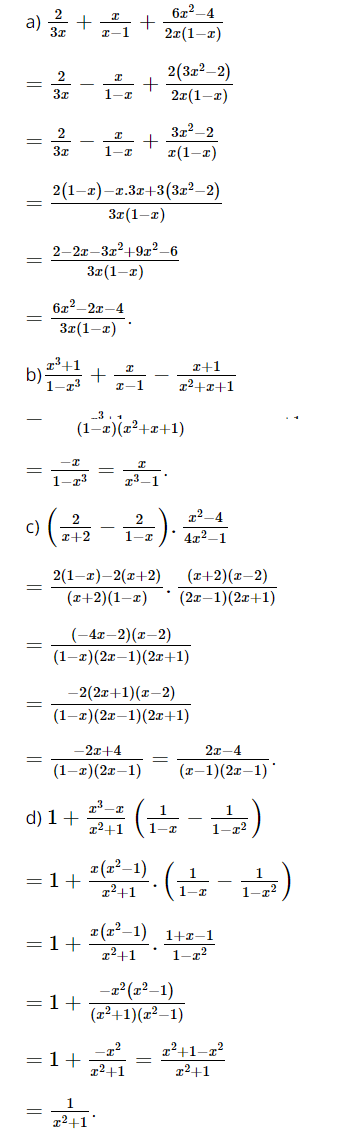
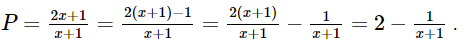
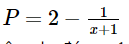 nên
nên 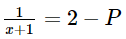 . Nếu x và P là số nguyên thì
. Nếu x và P là số nguyên thì 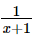 cũng là số nguyên, do đó x + 1 là ước của số 1 hay x + 1
cũng là số nguyên, do đó x + 1 là ước của số 1 hay x + 1 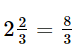 (giờ)
(giờ)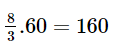 (km).
(km).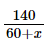 (giờ).
(giờ).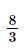 giờ, dừng nghỉ
giờ, dừng nghỉ 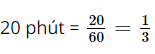 giờ.
giờ.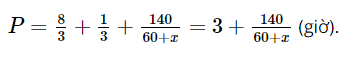
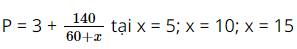
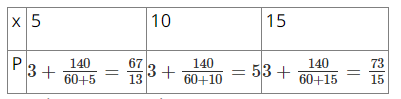
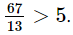
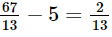
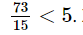
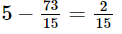 (giờ).
(giờ).