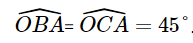Giải bài 7.30, 7.31, 7.32, 7.33, 7.34, 7.35 trang 54 SGK Toán 8 Kết nối tri thức tập 2Giải sách giáo khoa Toán lớp 8 trang Kết nối tri thức với cuộc sống tập 2: bài 7.30, 7.31, 7.32, 7.33, 7.34, 7.35. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y=x và y=−x+2. a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ Bài 7.30 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức Tìm hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1;-2) và có hệ số góc là 3. Phương pháp: Vì hàm số có hệ số góc là 3 => y = 3x + b Hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1;-2) , thay x = 1, y =−2 vào hàm số y = 3x + b rồi tìm ra b Suy ra công thức hàm số bậc nhất. Lời giải: Gọi hàm số cần tìm là y = ax + b (a ≠ 0). Vì đồ thị hàm số là đường thẳng có hệ số góc bằng 3 nên a = 3 hay y = 3x + b. Hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1; –2) , thay x = 1, y = –2 vào công thức hàm số, ta được: – 2 = 3 . 1 + b, tức là b = – 5.
Vậy ta có hàm số là y = 3x – 5. Bài 7.31 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là -2 và cắt trục hoành tại điểm có hoành độ bằng 3. Phương pháp: Vì hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là -2 => y = −2x + b Đường thẳng cắt trục hoành tại điểm có hoành độ bằng 3 => Đường thẳng đi qua điểm (3;0) Thay x=3; y=0 vào công thức hàm số: y = -2x + b tìm ra giá trị b. Suy ra công thức hàm số bậc nhất. Lời giải: Gọi hàm số cần tìm là y = ax + b (a ≠ 0). Vì hàm số có đồ thị là đường thẳng có hệ số góc là –2 nên a = – 2 hay y = –2x + b. Đường thẳng cắt trục hoành tại điểm có hoành độ bằng 3, có nghĩa là đường thẳng đi qua điểm (3; 0). Thay x = 3; y = 0 vào công thức hàm số ta có: 0 = –2 . 3 + b, hay b = 6. Vậy ta có hàm số y = –2x + 6. Bài 7.32 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức Hãy chỉ ra cặp đường thẳng song song với nhau và các cặp đường thẳng cắt nhau trong các đường thẳng sau y=−x+1; y=−2x+1; y=−2x+2; y=−x Phương pháp: Các cặp đường thẳng song song có a = a’; \(b \ne b'\) Các cặp đường thẳng cắt nhau có: \(a \ne a'\) Lời giải: +) Các cặp đường thẳng song song là: y = –x + 1 và y = –x (vì chúng có cùng hệ số góc là – 1); y = –2x + 1 và y = –2x + 2 (vì chúng có cùng hệ số góc là – 2). +) Các cặp đường thẳng cắt nhau là: y = –x + 1 và y = –2x + 2; y = –x và y = –2x + 1; y = –x + 1 và y = –2x + 1; y = –x và y = –2x + 2. Bài 7.33 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức Cho hàm số bậc nhất y=mx−5 và y=(2m+1)x+3. Tìm các giá trị của m để đồ thị của hai hàm số là: a) Hai đường thẳng song song b) Hai đường thẳng cắt nhau Phương pháp: Hai đường thẳng \(y = {\rm{ax + b(a}} \ne {\rm{0)}}\)và \(y = a'x + b'\left( {a' \ne 0} \right)\)song song với nhau khi a = a’; cắt nhau khi \(a \ne a'\) Lời giải: Hàm số y = mx – 5 là hàm số bậc nhất khi m ≠ 0. Hàm số y = (2m + 1)x + 3 là hàm số bậc nhất khi 2m + 1 ≠ 0 hay m ≠
a) Hai đường thẳng đã cho song song khi m = 2m + 1, suy ra m = –1. Giá trị này thỏa mãn điều kiện m ≠ 0 và m ≠
b) Hai đường thẳng đã cho cắt nhau khi m ≠ 2m + 1, suy ra m ≠ –1. Kết hợp với điều kiện, ta được m ≠ 0, m ≠ Bài 7.34 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y=−3x+1 và đi qua điểm (2;6) Phương pháp: Vì đồ thị hàm số bậc nhất là đường thẳng song song với đường thẳng y = -3x + 1 nên a = 3 Thay x = 2; y = 6 vào hàm số y = 3x + b ta tìm được b rồi suy ra công thức hàm số bậc nhất. Lời giải: Gọi y = ax + b là hàm số cần tìm (a ≠ 0). Vì đồ thị của hàm số song song với đường thẳng y = –3x + 1 nên a = –3 và b ≠ 1. Suy ra y = – 3x + 1 (b ≠ 1). Lại có, đồ thị hàm số là đường thẳng đi qua điểm (2; 6) nên ta có:
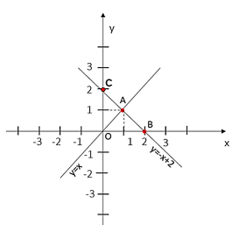
6 = –3 . 2 + b, suy ra b = 12 (thỏa mãn điều kiện b ≠ 1). Vậy hàm số cần tìm là y = –3x + 12. Bài 7.35 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y=x và y=−x+2 a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ b) Tìm giao điểm A của hai đường thẳng đã cho c) Gọi B là giao điểm của đường thẳng y=−x+2 và trục Ox. Chứng minh tam giác OAB vuông tại A, tức hai đường thẳng y=x và y=−x+2 vuông góc với nhau d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho Phương pháp: a) Vẽ hai đường thẳng y = x và y = −x + 2 trên mặt phẳng tọa độ bằng cách xác định hai điểm thuộc mỗi đường thẳng. b) Quan sát đồ thị hàm số y = x và y = 0x + 2 xác định tọa độ điểm A là giao điểm của hai đường thẳng đã cho. c) Lấy C là giao điểm của đường thẳng y = -x + 2 và trục Oy, chứng minh tam giác OBC vuông cân tại O. Chứng minh AB = AC => \(OA \bot AB\) hay tam giác OAB vuông cân tại A. d) Xác định hệ số góc của hai đường thẳng đã cho và tính tích của chúng Lời giải: a)* Xét đường thẳng y = x Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x. Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1). * Xét đường thẳng y = –x + 2 Cho y = 0 thì x = 2 nên điểm (2; 0) thuộc đường thẳng y = – x + 2. Cho x = 0 thì y = 2 nên điểm (0; 2 ) thuộc đường thẳng y = –x + 2. Đường thẳng y = – x + 2 đi qua hai điểm (2; 0) và (0; 2). b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho là: x = –x + 2 Giải phương trình này ta được x = 1. Từ đó suy ra y = 1. Vậy tọa độ giao điểm A(1; 1). c) Giao điểm của đường thẳng y = –x + 2 và trục Ox là B(2; 0). Gọi C là giao điểm của đường thẳng y = –x + 2 và trục Oy. Suy ra C(0; 2).
Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2). Xét hai tam giác OAB và OAC có: Cạnh OA chung; OB = OC;
Do đó ΔOAB = ΔOAC, từ đó suy ra AB = AC. Điều này chứng tỏ A là trung điểm của BC, mà ΔOBC cân tại O nên OA ⊥ AB, tức là ΔOAB vuông tại A. d) Đường thẳng y = x có hệ số góc bằng 1. Đường thẳng y = – x + 1 có hệ số góc bằng –1. Tích của hai hệ số góc của hai đường thẳng đã cho bằng –1. Từ câu c), ta có nhận xét: Hai đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng –1. Sachbaitap.com
Xem thêm tại đây:
Bài 29. Hệ số góc của đường thẳng
|
-

Giải bài 7.36, 7.37, 7.38, 7.39, 7.40 trang 56 SGK Toán 8 Kết nối tri thức tập 2
Giải sách giáo khoa Toán lớp 8 trang 56 Kết nối tri thức với cuộc sống tập 2: bài 7.36, 7.37, 7.38, 7.39, 7.40. Cho hai hàm số y=2x−1 và y=−x+2 a) Trong cùng mặt phẳng tọa độ Oxy, vẽ đồ thị của hai hàm số đã cho. b) Tìm tọa độ giao điểm của hai đồ thị trên.

 Tải ngay
Tải ngay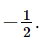
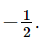 . Vậy giá trị m cần tìm là m = –1.
. Vậy giá trị m cần tìm là m = –1.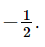
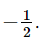 và m ≠ –1.
và m ≠ –1.