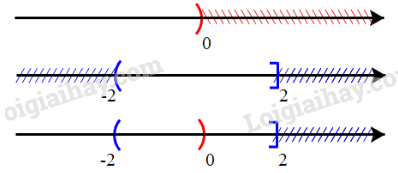
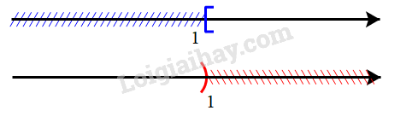
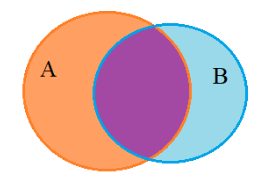
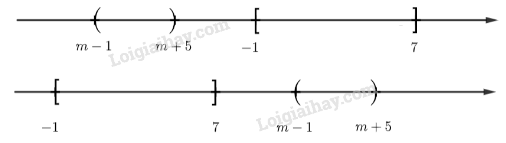
Giải SBT Toán 10 trang 14, 15, 16 Cánh Diều tập 1

Bài 18 trang 14 SBT Toán 10 - Cánh Diều

Cho tập hợp \(A = \left\{ {x \in \mathbb{N}|x \le 4} \right\}\). A là tập hợp nào sau đây?

A. \(\left\{ {0;1;2;3;4} \right\}\) 

B. \(\left( {0;4} \right]\) 

C. \(\left\{ {0;4} \right\}\) 

D. \(\left\{ {1;2;3;4} \right\}\)

Lời giải:

Đáp án đúng là A

Các phần tử thuộc tập hợp A là các số tự nhiên thỏa mãn bé hơn hoặc bằng 4. Do đó A = {0; 1; 2; 3; 4}.

Bài 19 trang 14 SBT Toán 10 - Cánh Diều

Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {3;4;5;6} \right\}\). Tập hợp \(A \cup B\) bằng

A. \(\left\{ {0;1;2;3;4;5;6} \right\}\)   

B. \(\left\{ {3;4} \right\}\)

C. \(\left\{ {0;1;2} \right\}\)   

D. \(\left\{ {5;6} \right\}\)

Lời giải:

Chọn A

Tập hợp A ∪ B gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B nên A ∪ B = {0; 1; 2; 3; 4; 5; 6}.

Bài 20 trang 14 SBT Toán 10 - Cánh Diều

Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {3;4;5;6} \right\}\). Tập hợp \(A\backslash B\) bằng:

A. \(\left\{ {0;1;2;3;4;5;6} \right\}\)

B. \(\left\{ {3;4} \right\}\)   

C. \(\left\{ {0;1;2} \right\}\) 

D. \(\left\{ {5;6} \right\}\)

Lời giải:

Đáp án đúng là C

Tập hợp A\B gồm các phần tử thuộc tập hợp A không thuộc tập hợp B nên A\B = {0; 1; 2}.

Bài 21 trang 14 SBT Toán 10 - Cánh Diều

Cho hai tập hợp \(A = \left( { - 3;3} \right],B = \left( {2; + \infty } \right)\). Tập hợp \(A \cap B\)bằng:

A. \(\left\{ { - 1;0;1;2;3} \right\}\)

B. \(\left[ { - 2; - 3} \right]\)

C. \(\left( { - 2;3} \right]\) 

D. \(\left( { - 3; + \infty } \right)\)

Lời giải:

Đáp án đúng là C

Ta có sơ đồ sau:

Tập hợp A∩B gồm các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B nên A∩B = ( – 2; 3].

Bài 22 trang 14 SBT Toán 10 - Cánh Diều

Cho tập hợp \(A = \left\{ {x \in \mathbb{R}|x \ge 2,x \ne 5} \right\}\). A là tập hợp nào sau đây?

A. \(\left( {2; + \infty } \right)\backslash \left\{ 5 \right\}\) 

B. \(\left[ {2;5} \right)\)

C. \(\left( {2;5} \right)\)

D. \(\left[ {2; + \infty } \right)\backslash \left\{ 5 \right\}\)

Lời giải:

Chọn D

Tập hợp A gồm các số thực lớn hơn hoặc bằng 2 và khác 5 nên A = [2; +∞) \ {5}.

Bài 23 trang 14 SBT Toán 10 - Cánh Diều

Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}| - 2 \le x \le 5} \right\},B = \left\{ {x \in \mathbb{Z}|{x^2} - x - 6 = 0} \right\}\). Tập hợp \(A\backslash B\) bằng:

A. \(\left( { - 2;3} \right)\)   

B. \(\left( { - 2;3} \right) \cup \left( {3;5} \right]\)   

C. \(\left( {3;5} \right]\) 

D. \(\left[ { - 2;5} \right]\backslash \left\{ 3 \right\}\)

Lời giải:

Chọn B

Ta có: A = {x ∈ ℝ| – 2 ≤ x ≤ 5} = [– 2; 5]

Xét phương trình \({x^2} - x - 6 = 0\)

\(\begin{array}{l} \Leftrightarrow \left( {x + 2} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ {_{x - 3 = 0}^{x + 2 = 0}} \right.\\ \Leftrightarrow \left[ {_{x = 3}^{x =  - 2}} \right.\end{array}\)

Vì –2; 3 ∈ ℤ nên B = {– 2; 3}.

Tập hợp A\B gồm các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B nên A\B = (– 2; 5] \ {-2;3} hay A\B = (– 2; 3) ∪ (3; 5].

Bài 24 trang 14 SBT Toán 10 - Cánh Diều

Cho tập hợp \(A = \left[ { - 1; + \infty } \right)\). Tập hợp \({C_\mathbb{R}}A\) bằng:

A. \(\left( { - 1; + \infty } \right)\) 

B. \(\left( { - \infty ; - 1} \right)\) 

C. \(\left( { - \infty ; - 1} \right]\)   

D. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)

Lời giải:

\({C_{\mathbb R}}A = \mathbb R{\rm{\backslash }}[1; + \infty ) = \left( { - \infty ; - 1} \right)\)

Chọn B

Bài 25 trang 14 SBT Toán 10 - Cánh Diều

Gọi A là tập nghiệm của đa thức\(P\left( x \right)\), B là tập nghiệm của đa thức \(Q\left( x \right)\), C là tập nghiệm của đa thức \(P(x).Q(x)\). C là tập hợp nào dưới đây?

A. \(A \cup B\)   

B. \(A \cap B\)

C. \(A\backslash B\) 

D. \(B\backslash A\)

Lời giải:

Chọn A

Xét \(P(x).Q(x)\) = 0

\( \Leftrightarrow \left[ {_{Q(x) = 0}^{P(x) = 0}} \right.\)

Do đó nghiệm của đa thức \(P(x).Q(x)\) là nghiệm của đa thức P(x) hoặc đa thức Q(x) nên \(C = A \cup B\).

Bài 26 trang 14 SBT Toán 10 - Cánh Diều

Gọi A là tập nghiệm của đa thức \(P\left( x \right)\), B là tập nghiệm của đa thức \(Q\left( x \right)\), D là tập nghiệm của đa thức \({P^2}(x) + {Q^2}(x)\). D là tập hợp nào dưới đây?

A. \(A \cup B\)       

B. \(A \cap B\)   

C. \(A\backslash B\)   

D. \(B\backslash A\)

Lời giải:

Chọn B

Xét P²(x) + Q²(x) = 0

Với mọi giá trị thực của x: P²(x) ≥ 0 và Q²(x) ≥ 0

nên để P²(x) + Q²(x) = 0 thì P(x) = Q(x) = 0.

Do đó nghiệm của đa thức \(P(x).Q(x)\)là nghiệm của đa thức P(x) vừa là nghiệm của đa thức Q(x) nên C = A∩B.

Bài 27 trang 14 SBT Toán 10 - Cánh Diều

Cho tập hợp \(X = \left\{ {a;b;c;d} \right\}\). Viết tất cả các tập con có ba phần từ của tập hợp X.

Lời giải:

Các tập hợp con có ba phần tử của tập hợp X là:

{a; b; c}, {a; b; d}, {a; c; d}, {b; c; d}.

Vậy các tập hợp con có ba phần tử của tập hợp X là: {a; b; c}, {a; b; d}, {a; c; d}, {b; c; d}.

Bài 28 trang 14 SBT Toán 10 - Cánh Diều

Cho ba tập hợp: A là tập hợp các tam giác; B là tập hợp các tam giác cân; C là tập hợp các tam giác đều. Dùng kí hiệu \( \subset \) để mô tả quan hệ của hai trong các tập hợp trên

Lời giải:

Ta có các tam giác cân, tam giác đều là tam giác. Do đó tập hợp B, tập hợp C là các tập hợp con của tập hợp A.

Ta lại có tam giác đều là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều nên tập hợp C là tập con của tập hợp B.

Vậy ta có quan hệ của các tập hợp đã cho là: C ⊂ B ⊂ A

Bài 29 trang 14 SBT Toán 10 - Cánh Diều

Dùng kí hiệu \( \subset \) để mô tả quan hệ của hai tập hợp khác nhau trong tập hợp sau: \(\left[ { - 1;3} \right];\left( { - 1;3} \right);\left[ { - 1;3} \right),\left( { - 1;3} \right],\left\{ { - 1;3} \right\}\)

Lời giải:

Ta có:

[– 1; 3] = {x ∈ ℝ| – 1 ≤ x ≤ 3}

(– 1; 3) = {x ∈ ℝ| – 1 < x < 3}

[– 1; 3) = {x ∈ ℝ| – 1 ≤ x < 3}

(– 1; 3] = {x ∈ ℝ| – 1 < x ≤ 3}

{– 1; 3}

Khi đó ta có:

(– 1; 3) ⊂ [– 1; 3]; [– 1; 3) ⊂ [– 1; 3]; (– 1; 3] ⊂ [– 1; 3]; {– 1; 3} ⊂ [– 1; 3].

(– 1; 3) ⊂ [– 1; 3); (– 1; 3) ⊂ (– 1; 3].

Bài 30 trang 15 SBT Toán 10 - Cánh Diều

Cho ba tập hợp sau: \(A = \left\{ {x \in \mathbb{N}|x \vdots 2} \right\},B = \left\{ {x \in \mathbb{N}|x \vdots 3} \right\};C = \left\{ {x \in \mathbb{N}|x \vdots 6} \right\}\)

a) Dùng kí hiệu \( \subset \)để mô tả quan hệ của hai trong các tập hợp trên

b) Xác định các tập hợp \(A \cap B,A \cup C,B \cap C\)

Lời giải:

a) Nếu x là một số chia hết cho 6 thì x chia hết cho 2 và x chia hết cho 3. Do đó tập hợp C là tập hợp con của tập hợp A và tập hợp B. Nên ta viết: C ⊂ A, C ⊂ B. 

Vậy C ⊂ A, C ⊂ B.

b) Tập hợp A∩B gồm các phần tử vừa thuộc tập hợp A và vừa thuộc tập hợp B nghĩa là các phần tử này vừa chia hết cho 2 và vừa chia hết cho 3 nên các phần tử của tập A∩B chia hết cho 6. Do đó A∩B = C.

Tập hợp A∪C gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp C nghĩa là các phần tử này hoặc chia hết cho 2 hoặc chia hết cho 6 mà chia hết cho 6 cũng là chia hết cho 2 nên các phần tử của tập A∪C chia hết cho 2. Do đó A∪C = A.

Tập hợp B∩C gồm các phần tử vừa chia hết cho 3 vừa chia hết cho 6 mà chia hết cho 3 cũng là chia hết cho 6 nên các phần tử của tập hợp B∩C chia hết cho 6. Do đó B∩C = C.

Vậy A∩B = C, A∪C = A, B∩C = C.

Bài 31 trang 15 SBT Toán 10 - Cánh Diều

Xác định các tập hợp sau

a) \(\left[ { - 2;3} \right] \cap \left( {0;5} \right)\) 

b) \(\left( { - 3;1} \right] \cap \left( {1; + \infty } \right)\)   

c) \(\left( { - \infty ;0} \right) \cup \left( { - 2;2} \right]\)

d) \(\left( { - \infty ;0} \right) \cup \left[ {0; + \infty } \right)\) 

e) \(\mathbb{R}\backslash \left[ {1; + \infty } \right)\)   

g) \(\left[ {3;5} \right]\backslash \left( {4;6} \right)\)

Lời giải:

a)

Vậy [– 2; 3] ∩ (0; 5) = (0; 3]

b)

Vậy [– 3; 1] ∩ (1; +∞) = ∅

c)

Vậy (– ∞; 0) ∪ (– 2; 2] = (– ∞; 2].

d)

Vậy (– ∞; 0) ∪ [0; +∞) = (– ∞; +∞) = ℝ

e)

Vậy ℝ \ [1; +∞) = (–∞; 1)

g)

Vậy [3; 5] \ (4; 6) = [3; 4]

Bài 31 trang 15 SBT Toán 10 - Cánh Diều

Cho A là một tập hợp. Xác định các tập hợp sau:

a) \(A \cap A\)   

b) \(A \cap \emptyset \)

c) \(A \cup A\)

d) \(A \cup \emptyset \)   

e) \(A\backslash A\)   

g) \(A\backslash \emptyset \)

Lời giải:

a) \(A \cap A = A\)

b)  \(A \cap \emptyset  = \emptyset \)

c)  \(A \cup A = A\)

d)  \(A \cup \emptyset  = A\)

e)  \(A\backslash A = \emptyset \)

g)  \(A\backslash \emptyset  = A\)

Bài 32 trang 15 SBT Toán 10 - Cánh Diều

Cho A là một tập hợp. Xác định các tập hợp sau:

a) \(A \cap A\)   

b) \(A \cap \emptyset \)

c) \(A \cup A\)

d) \(A \cup \emptyset \)   

e) \(A\backslash A\)   

g) \(A\backslash \emptyset \)

Lời giải:

a) \(A \cap A = A\)

b)  \(A \cap \emptyset  = \emptyset \)

c)  \(A \cup A = A\)

d)  \(A \cup \emptyset  = A\)

e)  \(A\backslash A = \emptyset \)

g)  \(A\backslash \emptyset  = A\)

Bài 33 trang 15 SBT Toán 10 - Cánh Diều

Cho tập hợp A. Có nhận xét gì về tập hợp B nếu:

a) \(A \cap B = A\)   

b) \(A \cap B = B\)   

c) \(A \cup B = A\)

d) \(A \cup B = B\)   

e) \(A\backslash B = \emptyset \)

g) \(A\backslash \emptyset  = B\)

Lời giải:

a) Ta có \(\left( {A \cap B} \right) \subset B \Rightarrow A \subset B\)

b) Ta có \(\left( {A \cap B} \right) \subset A \Rightarrow B \subset A\)

c) Ta có \(\left( {A \cup B} \right) \supset B \Rightarrow A \supset B\) hay B là tập con của A.

d) Ta có \(\left( {A \cup B} \right) \supset A \Rightarrow B \supset A\) hay A là tập con của B.

e) \(A\backslash B = \{ x \in A|x \notin B\}  = \emptyset  \Rightarrow \forall x \in A:x \in B \Leftrightarrow A \subset B\)

g) Ta có \(A\backslash \emptyset  = \left\{ {x \in A|x \notin \emptyset } \right\} = \left\{ {x \in A} \right\} = A\) suy ra \(A{\rm{\backslash }}\emptyset  = B \Leftrightarrow A = B\)

Bài 34 trang 15 SBT Toán 10 - Cánh Diều

Trong đợt văn nghệ chào mứng ngày 20/11, lớp 10A đăng kí tham gia hai tiết mục, đó là tốp ca và múa. Gọi A là tập hợp các học sinh tham gia hát tốp ca, B là tập hợp các học sinh tham gia múa, E là tập hợp các học sinh của lớp. Mô tả các tập hợp sau đây:

a) \(A \cap B\)   

b) \(A \cup B\)    

c) \(A\backslash B\)

d) \(E\backslash A\)

e) \(E\backslash \left( {A \cup B} \right)\)

Lời giải:

a) \(A \cap B\)là tập hợp các học sinh tham gia cả hai tiết mục hát tốp ca và tiết mục múa

b) \(A \cup B\) là tập hợp các học sinh tham gia ít nhất một tiết mục hát tốp ca hoặc múa.

c) \(A\backslash B\) là tập hợp các học sinh tham gia tiết mục hát tốp ca nhưng không tham gia tiết mục múa.

d) \(E\backslash A\) là tập hợp các học sinh của lớp 10A không tham gia tiết mục hát tốp ca.

e) \(E\backslash \left( {A \cup B} \right)\) là tập hợp các học sinh của lớp 10A không tham gia tiết mục nào trong hai tiết mục hát tốp ca và múa

Bài 35 trang 15 SBT Toán 10 - Cánh Diều

Lớp 10A có 27 học sinh tham gia ít nhất một trong hai câu lạc bộ bóng đá và cờ vua, trong đó có 19 học sinh tham gia câu lạc bộ bóng đá, 15 học sinh tham gia câu lạc bộ cờ vua.

a) Có bao nhiêu học sinh tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua?

b) Có bao nhiêu học sinh tham gia cả hai câu lạc bộ?

c) Biết trong lớp có 8 học sinh không tham gia câu lạc bộ nào trong hai câu lạc bộ trên. Lớp 10A có bao nhiêu học sinh?

Lời giải:

Gọi A là tập hợp các học sinh tham gia câu lạc bộ bóng đá,

B là tập hợp các học sinh tham gia câu lạc bộ cờ vua.

\( \Rightarrow A \cup B\) là tập hợp các học sinh tham gia ít nhất một trong hai câu lạc bộ bóng đá và cờ vua

\(A \cap B\) là tập hợp các học sinh tham gia cả hai câu lạc bộ

a) Ta có:  \(n\left( A \right) = 19,{\rm{ }}n\left( B \right) = 15,n(A \cup B) = 27\)

Tập hợp học sinh tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua là tập A\B (phần màu cam) hay chính là tập hợp \((A \cup B)\backslash B\)

Số phần tử của tập hợp \((A \cup B)\backslash B\) là số học sinh tham gia một trong hai câu lạc bộ trừ đi số học sinh tham gia câu lạc bộ cờ vua.

\(n((A \cup B)\backslash B) = n(A \cup B)--n\left( B \right) = 27--15 = 12.\)

Vậy số học sinh tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua là 12 học sinh.

b) Tập hợp số học sinh tham gia cả hai câu lạc bộ là tập \(A \cap B\).

Số phần tử của tập hợp \(A \cap B\)bằng số học sinh tham gia câu lạc bộ bóng đá trừ đi số học sinh chỉ tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua.

\( \Rightarrow n(A \cap B) = n\left( A \right)--n(A{\rm{\backslash }}B) = 19--12 = 7.\)

Vậy số học sinh tham gia cả hai câu lạc bộ là 7 học sinh

c) Lớp 10A gồm các học sinh tham gia ít nhất một trong hai câu lạc bộ và các học sinh không tham gia câu lạc bộ nào.

=> số học sinh của lớp 10A là: 27 + 8 = 35 (học sinh)

Vậy số học sinh của lớp 10A là 35 học sinh.

Bài 36 trang 15 SBT Toán 10 - Cánh Diều

Tìm \(D = E \cap G\), biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:

a) \(5x - 2 > 0\)và \(3x + 7 \ge 0\)

b) \(2x + 3 > 0\)và \(5x - 9 \le 0\)

c) \(9 - 3x \ge 0\)và \(12 - 3x < 0\)

Lời giải:

a) Ta có: \(5x - 2 > 0 \Leftrightarrow x > \frac{2}{5}\)           \( \Rightarrow E = \left\{ {x \in \mathbb{R}\left| {x > \frac{2}{5}} \right.} \right\} = \left( {\frac{2}{5}; + \infty } \right)\)

Lại có: \(3x + 7 \ge 0 \Leftrightarrow x \ge  - \frac{7}{3}\)    \( \Rightarrow G = \left\{ {x \in \mathbb{R}\left| {x \ge  - \frac{7}{3}} \right.} \right\} = \left[ { - \frac{7}{3}; + \infty } \right)\)

Tập hợp \(E \cap G\) là tập hợp các số thực x sao cho \(x > \frac{2}{5}\) và \(x \ge \frac{7}{3}\)

Hay \(E \cap G = \left\{ {x \in \mathbb{R}\left| {x > \frac{2}{5};x \ge  - \frac{7}{3}} \right.} \right\} = \left\{ {x \in \mathbb{R}\left| {x > \frac{2}{5}} \right.} \right\} = E\)

Vậy \(D = E\)

b) Ta có: \(2x + 3 > 0 \Leftrightarrow x >  - \frac{3}{2}\)\( \Rightarrow E = \left\{ {x \in \mathbb{R}\left| {x >  - \frac{3}{2}} \right.} \right\} = \left( { - \frac{3}{2}; + \infty } \right)\)

Lại có: \(5x - 9 \le 0 \Leftrightarrow x \le \frac{9}{5}\)          \( \Rightarrow G = \left\{ {x \in \mathbb{R}\left| {x \le \frac{9}{5}} \right.} \right\} = \left( { - \infty ;\frac{9}{5}} \right]\)

Tập hợp \(E \cap G\) là tập hợp các số thực x sao cho \(x >  - \frac{3}{2}\) và \(x \le \frac{9}{5}\)

Hay \(E \cap G = \left\{ {x \in \mathbb{R}\left| { - \frac{3}{2} < x \le \frac{9}{5}} \right.} \right\} = \left( { - \frac{3}{2};\frac{9}{5}} \right]\)

\( \Rightarrow D = E \cap G = \left( { - \frac{3}{2};\frac{9}{5}} \right]\)

c) Ta có: \(9 - 3x \ge 0 \Leftrightarrow x \le 3\) \( \Rightarrow E = \left\{ {x \in \mathbb{R}\left| {x \le 3} \right.} \right\} = \left( { - \infty ;3} \right]\)

Lại có: \(12 - 3x < 0 \Leftrightarrow x > 4\)      \( \Rightarrow G = \left\{ {x \in \mathbb{R}\left| {x > 4} \right.} \right\} = \left( {4; + \infty } \right)\)

Tập hợp \(E \cap G\) là tập hợp các số thực x sao cho \(x > 4\) và \(x \le 3\)

hay \(E \cap G = \left\{ {x \in \mathbb{R}\left| {4 < x \le 3} \right.} \right\} = \emptyset \)

Vậy \(D = \emptyset \)

Bài 37 trang 15 SBT Toán 10 - Cánh Diều

Tìm các tập hợp \(A = \left[ { - 1;7} \right],B = \left( {m - 1;m + 5} \right)\) với m là một tham số thực. Tìm m để

a) \(B \subset A\)

b) \(A \cap B = \emptyset \)

Lời giải:

a)

Để \(B \subset A\) thì \(\left\{ {\begin{array}{*{20}{c}}{m - 1 \ge  - 1}\\{m + 5 \le 7}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ge 0}\\{m \le 2}\end{array}} \right.} \right. \Leftrightarrow 0 \le m \le 2\)

Vậy với m thỏa mãn \(0 \le m \le 2\) thì \(B \subset A\)

b)

Để \(A \cap B = \emptyset \) thì \(\left[ {\begin{array}{*{20}{c}}{m - 1 \ge 7}\\{m + 5 \le  - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge 8}\\{m \le  - 6}\end{array}} \right.\)

Vậy với m thỏa mãn \(m \le  - 6\) hoặc \(m \ge 8\) thì \(A \cap B = \emptyset \)

Bài 38 trang 15 SBT Toán 10 - Cánh Diều

Cho \(A = \left[ {m;m + 2} \right]\)và \(B = \left[ {n;n + 1} \right]\) với m, n là các tham số thực. Tìm điều kiện của các số m và n để tập hợp \(A \cap B\)chứa đúng một phần tử.

Lời giải:

Để tập hợp \(A \cap B\) chứa đúng một phần tử thì \(\left[ {\begin{array}{*{20}{c}}{m + 2 = n}\\{n + 1 = m}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = n - 2}\\{m = n + 1}\end{array}} \right.\)

Vậy với \(m = n - 2\) hoặc \(m = n + 1\) thì  \(A \cap B\) chứa đúng một phần tử

Bài 39 trang 16 SBT Toán 10 - Cánh Diều

Cho \(A = \left( { - \infty ;m + 1} \right),B = \left[ {3; + \infty } \right)\) với m là một tham số thực. Tìm m để:

a) \(A \cup B = \mathbb{R}\)   

b) \(A \cap B\)chứa đúng 5 số nguyên

Lời giải:

a) Trường hợp 1: \(3 < m + 1\)

=> \(A \cup B = \mathbb{R}\)

Tường hợp 2: \(m + 1 < 3\)

=> \(A \cup B = \mathbb{R} \backslash  [m+1;3) \)

Trường hợp 3: \(m + 1 = 3\)

=> \(A \cup B = \mathbb{R}\)

Để \(A \cup B = \mathbb{R}\) thì \(m + 1 \ge 3 \Leftrightarrow m \ge 2\)

Vậy với \(m \ge 2\) thì \(A \cup B = \mathbb{R}\)

b) Ta có: \(A \cap B = \{ x \in \mathbb{R}|x < m + 1\) và \(x \ge 3\}  = \{ x \in \mathbb{R}|3 \le x < m + 1\} \)

Để \(A \cap B \ne \emptyset \)thì \(m + 1 \ge 3 \Leftrightarrow m \ge 2\quad (1)\)

Khi đó \(A \cap B = \left[ {3;m + 1} \right)\)

Để tập hợp \(A \cap B\) chưa đúng 5 số nguyên thì \(A \cap B = \left\{ {3;4;5;6;7} \right\}\) tức là \(7 < m + 1 \le 8\)(2)

Kết hợp (1) và (2) ta được \(6 < m \le 7\)

Vậy với \(6 < m \le 7\)thì\(A \cap B\) chứa đúng 5 số nguyên

Bài 40 trang 15 SBT Toán 10 - Cánh Diều

Biểu diễn tập hợp \(A = \left\{ {x \in \mathbb{R}|{x^2} \ge 9} \right\}\) thành hợp các nửa khoảng

Lời giải:

Ta có:  \({x^2} \ge 9\)\( \Leftrightarrow \left| x \right| \ge 3 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \ge 3}\\{x \le  - 3}\end{array}} \right.\)

Suy ra \(A = \{ x \in \mathbb{R}\left| {x \le  - 3} \right.\) hoặc \(x \le  - 3\}  = \{ x \in \mathbb{R}\left| {x \le  - 3\}  \cup } \right.\{ x \in \mathbb{R}\left| {x \ge 3\} } \right. = \left( { - \infty ; - 3} \right] \cup \left[ {3; + \infty } \right)\)

Vậy \(A = \left( { - \infty ; - 3} \right] \cup \left[ {3; + \infty } \right)\)

Sachbaitap.com