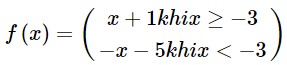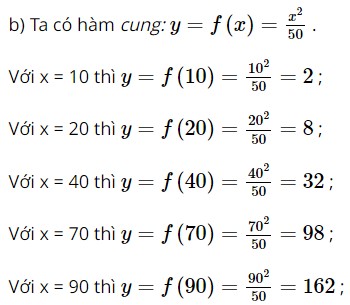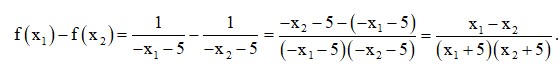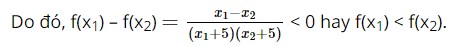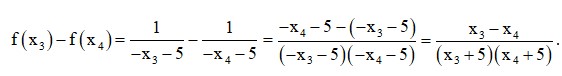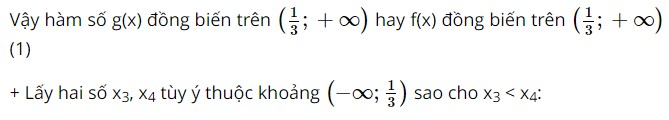Giải SBT Toán 10 trang 45, 46, 47 Chân trời sáng tạo tập 1

Bài 1 trang 45 SBT Toán 10 - Chân trời sáng tạo

Tìm tập xác định của các hàm số sau:

a) \(f\left( x \right) = \frac{{4x - 1}}{{\sqrt {2x - 5} }}\)

b) \(f\left( x \right) = \frac{{2 - x}}{{\left( {x + 3} \right)\left( {x - 7} \right)}}\)

c) \(f\left( x \right) = \left\{ \begin{array}{l}\frac{1}{{x - 3}}{\rm{ }}\quad \;\;x \ge {\rm{0  }}\\1{\rm{        }}\quad {\rm{ }}x < 0\end{array} \right.\)

Lời giải:

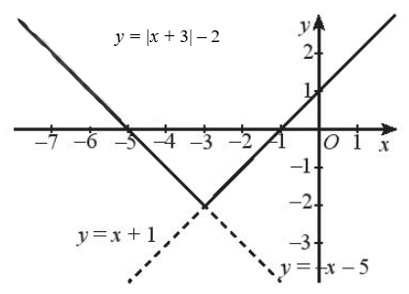
Vậy tập xác định của hàm số là D = ℝ \ {– 3; 7}.

c) Hàm số lấy giá trị bằng 1 khi x < 0 nên hàm số xác định với mọi x < 0.

Khi x ≥ 0, hàm số xác định khi và chỉ khi x – 3 ≠ 0 ⇒ x ≠ 3.

Vậy tập xác định của hàm số là D = ℝ \ {3}.

Bài 2 trang 45 SBT Toán 10 - Chân trời sáng tạo

Vẽ đồ thị các hàm số sau:

a) \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}{\rm{       }}\quad x \le 2{\rm{  }}\\x + 2{\rm{   }}\quad x > 2\end{array} \right.\) 

b) \(f\left( x \right) = \left| {x + 3} \right| - 2\)

Phương pháp:

Bước 1: Vẽ đồ thị của hàm số với công thức thứ nhất theo điều kiện đi kèm của x

Bước 2: Vẽ đồ thi của hàm số với công thức và điều kiện còn lại

Lời giải:

a) + Vẽ đồ thị hàm số g(x) = x2 và giữ lại phần đồ thị ứng với x ≤ 2:

Đồ thị hàm số g(x) = x2 là một parabol có đỉnh là gốc tọa độ O, trục đối xứng là trục Oy, đồ thị có bề lõm hướng lên trên, đi qua các điểm (1; 1), (– 1; 1), (2; 4), (– 2; 4).

Ta giữ lại phần đồ thị nằm bên trái đường thẳng x = 2:

+ Vẽ đồ thị hàm số h(x) = x + 2 và giữ lại phần đồ thị ứng với x > 2.

Đồ thị hàm số h(x) = x + 2 là một đường thẳng đi qua hai điểm (0; 2) và (– 2; 0).

Ta giữ lại phần đường thẳng nằm bên phải đường thẳng x = 2.

Ta được đồ thị cần vẽ như hình sau:

b) Với x + 3 ≥ 0 ⇔ x ≥ – 3, ta có: |x + 3| – 2 = x + 3 – 2 = x + 1.

Với x + 3 < 0 ⇔ x < – 3, ta có: |x + 3| – 2 = – (x + 3) – 2 = – x – 3 – 2 = – x – 5.

Khi đó ta có:

Ta vẽ đồ thị hàm số g(x) = x + 1 và giữ lại phần đồ thị ứng với x ≥ – 3: Đồ thị hàm số g(x) = x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; 0).

Ta vẽ đồ thị hàm số h(x) = – x – 5 và giữ lại phần đồ thị ứng với x < – 3: Đồ thị hàm số h(x) = – x – 5 là đường thẳng đi qua hai điểm (– 5; 0) và (– 3; – 2).

Ta được đồ thị của hàm số cần vẽ như hình sau:

Bài 3 trang 46 SBT Toán 10 - Chân trời sáng tạo

Trong kinh tế thị trường, lượng cầu và lượng cung là hai khái niệm quan trọng. Lượng cầu chỉ khả năng về số lượng sản phẩm cần mua của bên mua (người tiêu dùng), tùy theo đơn giá bán sản phẩm; còn lượng cung chỉ khả năng cung cấp số lượng sản phẩm này cho thị trường của bên bán (nhà sản xuất) cũng phụ thuộc vào đơn giá bán sản phẩm

Người ta khảo sát nhu cầu của thị trường đối với sản phẩm A theo đơn giá cúa sản phẩm này và thu được bảng sau:

a) Hãy cho biết tại sao bảng giá trị trên xác định một hàm số? Hãy tìm tập xác định và tập giá trị của hàm số đó (gọi là hàm cầu)

b) Giả sử lượng cung của sản phẩm A tuân theo công thức   \(y = f\left( x \right) = \frac{{{x^2}}}{{50}}\)

trong đó x là đơn giá sản phẩm A và y là lượng cung ứng với đơn giá này. Hãy điền các giá trị của hàm số \(f\left( x \right)\) (gọi là hàm cung) vào bảng sau

c) Ta nói thị trường của một sản phẩm là cân bằng khi lượng cung và lượng cầu bằng nhau. Hãy tìm đơn giá x của sản phẩm A khi thị trường cân bằng

Lời giải:

a) Từ bảng đã cho ta có thể thấy với mỗi mức đơn giá, đều có duy nhất một giá trị về lượng cầu. Do vậy bảng giá trị cho ở đề bài xác định một hàm số.

Hàm số này có tập xác định D = {10; 20; 40; 70; 90} và có tập giá trị T = {338; 288; 200; 98; 50}.

Vậy ta điền được bảng sau:

c) Từ hai bảng giá trị của lượng cung và lượng cầu, ta tìm được giá trị x = 70 thì lượng cung và lượng cầu đều bằng 98.

Vậy thị trường của sản phẩm A cân bằng khi đơn giá của sản phẩm A là 70 000 (đồng).

Bài 4 trang 46 SBT Toán 10 - Chân trời sáng tạo

Tìm khoảng đồng biến và nghịch biến của các hàm số sau:

a) \(f\left( x \right) = \frac{1}{{ - x - 5}}\)

b) \(f\left( x \right) = \left| {3{\rm{x}} - 1} \right|\)

Phương pháp:

Bước 1: Xác định tập xác định của hàm số

Bước 2: Lấy \({x_1},{x_2}\) tùy ý thuộc tập xác định, thay vào f(x) tính và so sánh biết:

Với hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) thì ta có

+) Hàm số đồng biến trên khoảng (a; b) nếu \(\forall {x_1},{x_2} \in \left( {a;b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)

+) Hàm số ngịch biến trên khoảng (a; b) nếu \(\forall {x_1},{x_2} \in \left( {a;b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)

Bước 3: Kết luận

Lời giải:

a) Tập xác định của hàm số là: D = ℝ \ {– 5}.

+ Xét khoảng (– ∞; – 5):

Lấy hai số x1, x2 tùy ý thuộc (– ∞; – 5) sao cho x1 < x2.

Ta có:

Vì x1, x2 ∈ (– ∞; – 5) nên x1 + 5 < 0 và x2 + 5 < 0.

Lại có: x1 < x2 nên x1 – x2 < 0.

Vậy hàm số đồng biến trên khoảng (– ∞; – 5). (1)

+ Xét khoảng (– 5; + ∞):

Lấy hai số x3, x4 tùy ý thuộc (– 5; + ∞) sao cho x3 < x4.

Ta có:

Vì x3, x4 ∈ (– 5; + ∞) nên x3 + 5 > 0 và x4 + 5 > 0.

Lại có: x3 < x4 nên x3 – x4 < 0.

ậy hàm số đồng biến trên khoảng (– 5; + ∞). (2)

Từ (1) và (2) suy ra hàm số đã cho đồng biến trên các khoảng (– ∞; – 5) và (– 5; + ∞).

Khi đó ta có:

Ta có: f(x1) – f(x2) = (3x1 – 1) – (3x2 – 1) = 3(x1 – x2) < 0 (do x1 < x2 nên x1 – x2 < 0).

Suy ra f(x1) < f(x2).

Ta có: f(x3) – f(x4) = (– 3x3 + 1) – (– 3x4 + 1) = 3(x4 – x3) > 0 (do x3 < x4 nên x4 – x3 > 0).

Suy ra f(x3) > f(x4).

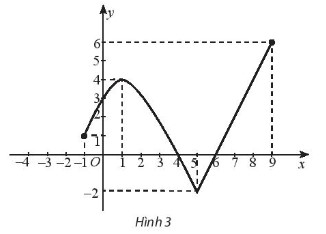
Bài 5 trang 46 SBT Toán 10 - Chân trời sáng tạo

Tìm khoảng đồng biến, nghịch biến của các hàm số sau:

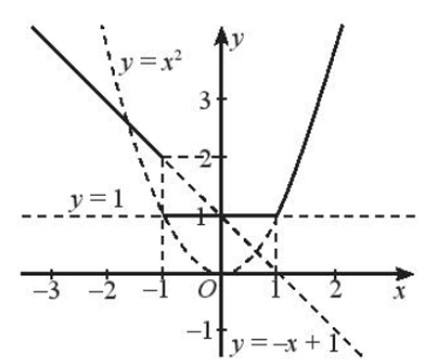
Phương pháp:

Dựa vào hình vẽ, xác định khoảng đồng biến là khoảng đồ thị hàm số đi lên, và nghịch biến là khoảng đồ thị hàm số đi xuống

Lời giải:

uan sát Hình 3 ta thấy:

- Đồ thị hàm số có dạng đi lên từ điểm có tọa độ (– 1; 1) đến điểm có tọa độ (1; 4) nên hàm số đồng biến trên khoảng (– 1; 1);

- Đồ thị hàm số có dạng đi xuống từ điểm có tọa độ (1; 4) đến điểm có tọa độ (5; – 2) nên hàm số nghịch biến trên khoảng (1; 5);

- Đồ thị hàm số có dạng đi lên từ điểm có tọa độ (5; – 2) đến điểm có tọa độ (9; 6) nên hàm số đồng biến trên khoảng (5; 9).

Vậy hàm số có đồ thị như Hình 3 đồng biến trên các khoảng (– 1; 1) và (5; 9), nghịch biến trên khoảng (1; 5).

Bài 6 trang 47 SBT Toán 10 - Chân trời sáng tạo

Vẽ đồ thị hàm số sau:  \(f\left( x \right) = \left\{ \begin{array}{l} - x + 1{\rm{   khi }}x <  - 1\\1{\rm{           khi }} - 1 \le x < 1{\rm{ }}\\{x^2}{\rm{         khi }}x \ge 1\end{array} \right.\)

Lời giải:

Ta vẽ đồ thị hàm số g(x) = – x + 1 trên khoảng (– ∞; – 1), đồ thị hàm số h(x) = 1 trên nửa khoảng [– 1; 1), đồ thị hàm số k(x) = x2 trên nửa khoảng [1; + ∞).

Khi đó ta có đồ thị hàm số f(x) như sau:

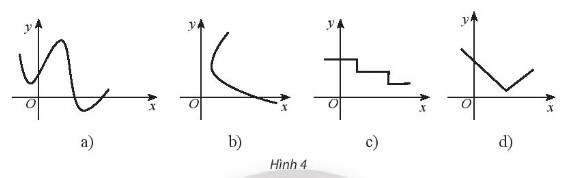
Bài 7 trang 47 SBT Toán 10 - Chân trời sáng tạo

Trong các đường biểu diễn được cho trong hình 4, chỉ ra trường hợp không phải là đồ thị hàm số và giải thích vì sao

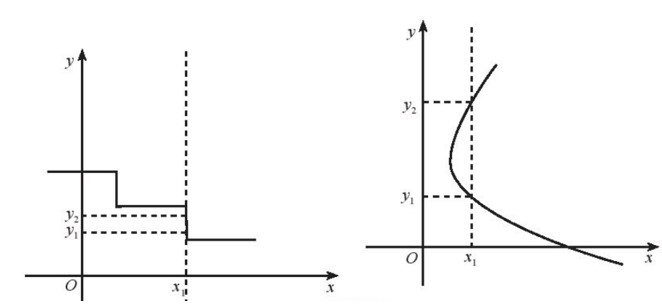
Lời giải:

Hai đường biểu diễn ở Hình b và Hình c không phải là đồ thị hàm số vì ứng với một giá trị của x, có đến hai (hay nhiều) giá trị khác nhau của y (quan sát trên hình sau).

Sachbaitap.com