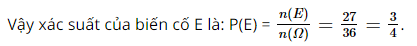Giải SBT Toán 10 trang 48, 49, 50 Cánh Diều tập 2

Bài 37 trang 48 SBT Toán 10 - Cánh Diều

Số quy tròn của số gần đúng 38,4753701 với độ chính xác 0,005 là:

A. 38,47                                                     B. 38,48

C. 38,49                                                     D. 38,5

Phương pháp:

Hàng lớn nhất của độ chính xác là \(d = 0,005\) là hàng phần nghìn, nên ta quy tròn a đến hàng phần trăm

Lời giải:

Do 0,001 < d = 0,005 < 0,01 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng phần trăm.

Vì thế, ta quy tròn số 38,4753701 đến hàng phần trăm.

Vậy số quy tròn của 38,4753701 là 38,48.

Do đó ta chọn phương án B.

Bài 38 trang 48 SBT Toán 10 - Cánh Diều

Số quy tròn của số gần đúng -97 186 với độ chính xác 50 là:

A. -97 100              B. -97 000              C. -97 200              D. -97 300

Phương pháp:

Hàng lớn nhất của độ chính xác là \(d = 50\) là hàng chục, nên ta quy tròn a đến hàng trăm

Lời giải:

Do 10 < d = 50 < 100 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng trăm.

Vì thế, ta quy tròn số –97 186 đến hàng trăm.

Vậy số quy tròn của –97 186 là –97 200.

Do đó ta chọn phương án C.

Bài 39 trang 48 SBT Toán 10 - Cánh Diều

Cho mẫu số liệu: 3 4 6 9 13

a) Trung vị của mẫu số liệu trên là:

A. 7              B. 6              C. 6,5           D. 8

b) Số trung bình cộng của mẫu số liệu trên là:

A. 7              B. 6              C. 6,5           D. 8

c) Khoảng biến thiên của mẫu số liệu trên là:

A. 7              B. 6              C. 1              D. 10

d) Tứ phân vị của mẫu số liệu trên là:

A. \({Q_1} = 4;{Q_2} = 6;{Q_3} = 9\)                    B. \({Q_1} = 3,5;{Q_2} = 6;{Q_3} = 9\)           

C. \({Q_1} = 4;{Q_2} = 6;{Q_3} = 11\)                  D. \({Q_1} = 3,5;{Q_2} = 6;{Q_3} = 11\)

e) Khoảng tứ phân vị của mẫu số liệu trên là:

A. 7,5           B. 6              C. 1              D. 10

g) Phương sai của mẫu số liệu trên là:

A. 66            B. 13,2                   C. \(\sqrt {66} \)    D. \(\sqrt {13,2} \)

h) Độ lệch chuẩn của mẫu số liệu trên là:

A. 66            B. 13,2                   C. \(\sqrt {66} \)    D. \(\sqrt {13,2} \)

Lời giải:

3 4 6 9 13

a) Vì \(n = 5\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 6\) là tứ phân vị

Chọn B.

b) Số trung bình của mẫu số liệu là: \(\overline x  = \frac{{3 + 4 + 6 + 9 + 13}}{5} = 7\)

Chọn A.

c) Số cao nhất và thấp nhất lần lượt là 13 và 3 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 13 - 3 = 10\)

Chọn D.

d)

+ Vì \(n = 5\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 6\) là tứ phân vị

+ Tứ phân vị thứ nhất là trung vị của 2 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {3 + 4} \right):2 = 3,5\)

+ Tứ phân vị thứ ba là trung vị của 2 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 13} \right):2 = 11\)

Chọn D.

e) + Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 11 - 3,5 = 7,5\)

Chọn A.

g) Phương sai: \({S^2} = \frac{1}{5}({3^2} + {4^2} + {6^2} + {9^2} + {13^2}) - {7^2} = 13,2\)

Chọn B.

h) Độ lệch chuẩn: \(S = \sqrt {{S^2}}  = \sqrt {13,2} \)

Chọn D.

Bài 40 trang 49 SBT Toán 10 - Cánh Diều

Tung một đồng xu hai lần liên tiếp. Xác suất của biến cố “Kết quả của hai lần tung lác khác nhau” là:

A. \(\frac{1}{2}\)             B. \(\frac{1}{4}\)             C. \(\frac{3}{4}\)                  D. \(\frac{1}{3}\)

Phương pháp:

Xác suất của biến cố A là một số, kí hiệu \(P\left( A \right)\) được xác định bởi công thức: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\), trong đó \(n\left( A \right)\) và \(n\left( \Omega  \right)\) lần lượt là kí hiệu số phần tử của tập A và \(\Omega \)

Lời giải:

Không gian mẫu trong trò chơi tung đồng xu hai lần liên tiếp là tập hợp:

Ω = {SS; SN; NS; NN}.

Do đó n(Ω) = 4.

Gọi A là biến cố “Kết quả của hai lần tung là khác nhau”.

Các kết quả thuận lợi cho biến cố A là: SN; NS.

Tức là, A = {SN; NS}.

Vì thế, n(A) = 2.

Do đó ta chọn phương án A.

Bài 41 trang 49 SBT Toán 10 - Cánh Diều

Gieo một xúc sắc hai lần liên tiếp. Xác suất của biến cố “Tích số chấm trong hai lần gieo là số chẵn” là:

A. \(\frac{1}{2}\)             B. \(\frac{1}{4}\)             C. \(\frac{3}{4}\)                  D. \(\frac{1}{3}\)

Phương pháp:

Xác suất của biến cố A là một số, kí hiệu \(P\left( A \right)\) được xác định bởi công thức: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\), trong đó \(n\left( A \right)\) và \(n\left( \Omega  \right)\) lần lượt là kí hiệu số phần tử của tập A và \(\Omega \)

Biến cố đối của biến cố A là biến cố không xảy ra A, kí hiệu là \(\overline A \) và \(P\left( {\overline A } \right) + P\left( A \right) = 1\)

Lời giải:

Không gian mẫu của trò chơi gieo một xúc xắc hai lần liên tiếp là tập hợp:

Ω = {(i; j) | i; j = 1; 2; 3; 4; 5; 6}.

Do đó n(Ω) = 36.

Gọi E là biến cố “Tích số chấm trong hai lần gieo là số chẵn”.

Các kết quả thuận lợi cho biến cố E là: (1; 2), (1; 4), (1; 6), (2; 1), (2; 2), (2; 3), (2; 4), (2; 5), (2; 6), (3; 2), (3; 4), (3; 6), (4; 1), (4; 2), (4; 3), (4; 4), (4; 5), (4; 6), (5; 2), (5; 4), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6).

Vì thế, n(E) = 27.

Do đó ta chọn phương án C.

Bài 42 trang 49 SBT Toán 10 - Cánh Diều

Bác Ngân có một chiếc ddienj thoại cũ để mật khẩu 6 chữ số. Bác đã quên mật khẩu chính xác và chỉ nhớ các chữ số đó là đôi một khác nhau. Xác suất để bác Ngân bấm đúng mật khẩu của chiếc điệnt hoại cũ đó trong 1 lần là:

A. \(\frac{1}{{A_{10}^6}}\)                B. \(\frac{1}{{C_{10}^6}}\)           C. \(\frac{{A_{10}^6}}{{6!}}\)                 D. \(\frac{{6!}}{{A_{10}^6}}\)

Lời giải:

Chọn 6 trong 10 chữ số và sắp xếp 6 chữ số đó \( \Rightarrow n\left( \Omega  \right) = A_{10}^6\)

+ \(n\left( A \right) = 1\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{1}{{A_{10}^6}}\)

Chọn A.

Bài 43 trang 49 SBT Toán 10 - Cánh Diều

Bảng dưới đây thống kê sản lượng thủy sản của VN từ năm 2013 đến năm 2020 (đơn vị: triệu tấn)

 a) Viết mẫu số liệu thống kê sản lượng thủy sản của VN nhận đươc từ bảng trên

b) Tìm số trung bình cộng, trung bị và tứ phân vị của mẫu số liệu đó

c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó

d) Tìm phương sai và độ lệch chuẩn của mẫu số liệu đó

Lời giải:

a) Viết mẫu số liệu thống kê sản lượng thủy sản của VN nhận đươc từ bảng trên: 6,053; 6,319; 6,563; 6,728; 7,279; 7,743; 8,150; 8,140

b)

+ Số trung bình của mẫu số liệu là: \(\overline x  = \frac{{6,053 + 6,319 + 6,563 + 6,728 + 7,279 + 7,743 + 8,150 + 8,140}}{8} = 7,155625\)

+ Vì \(n = 8\) là số chẵn nên tứ phân vị thứ hai là: \({Q_2} = \left( {6,728 + 7,279} \right):2 = 7,0035\) là tứ phân vị

+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {6,319 + 6,563} \right):2 = 6,441\)

+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {7,743 + 8,150} \right) = 7,9465\)

c)

+ Số cao nhất và thấp nhất lần lượt là 8,140 và 6,053 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 8,140 - 6,053 = 2,357\)

+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 7,9465 - 6,441 = 1,5055\)

d)

+ Phương sai: \({S^2} = \frac{1}{8}(6,{053^2} + 6,{319^2} + ... + 8,{140^2}) - 7,{155625^2} \approx 0,67\)

+ Độ lệch chuẩn: \(S = \sqrt {{S^2}}  \approx \sqrt {0,67}  \approx 0,82\)

Bài 44 trang 50 SBT Toán 10 - Cánh Diều

Một hội thảo quốc tế gồm 12 học sinh đến từ các nước: VN, Nhật Bản, Singapore, Ấn Độ, Hàn Quốc, Brasil, Canada, Tây Ban Nha, Đức, Pháp, Nam Phi, Cameroon, mỗi nước chỉ có đúng 1 học sinh. Chọn ra ngẫu nhiên 2 học sinh trong nhóm học sinh quốc tế để tham gia BTC:

Tính xác suất của mỗi biến cố sau:

a) A: “Hai học sinh được chọn ra đến từ châu Á”

b) B: “Hai học sinh được chọn ra đến từ châu Âu”

c) C: “Hai học sinh được chọn ra đến từ châu Mĩ”

d) D: “Hai học sinh được chọn ra đến từ châu Phi”

Lời giải:

Chọn 2 học sinh từ 12 học sinh \( \Rightarrow \) tổ hợp chập 2 của 12 \( \Rightarrow n\left( \Omega  \right) = C_{12}^2 = 66\)

a) A: “Hai học sinh được chọn ra đến từ châu Á”:

Có 5 nước châu Á: Việt Nam, Nhật Bản, Singapore, Ấn Độ, HQ

\( \Rightarrow n\left( A \right) = C_5^2 = 10\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{10}}{{66}} = \frac{5}{{33}}\)

b) B: “Hai học sinh được chọn ra đến từ châu Âu”: Có 3 nước châu Âu: TBN, Đức, Pháp \( \Rightarrow n\left( B \right) = C_3^2 = 3\)

\( \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{3}{{66}} = \frac{1}{{22}}\)

c) C: “Hai học sinh được chọn ra đến từ châu Mĩ”: Có 2 nước châu Mĩ: Brasil, Canada \( \Rightarrow n\left( C \right) = C_2^2 = 1\)

\( \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega  \right)}} = \frac{1}{{66}}\)

d) D: “Hai học sinh được chọn ra đến từ châu Phi”: Có 2 nước châu Phi: Nam Phi, Cameroon \( \Rightarrow n\left( D \right) = C_2^2 = 1\)

\( \Rightarrow P\left( D \right) = \frac{{n\left( D \right)}}{{n\left( \Omega  \right)}} = \frac{1}{{66}}\)

Bài 45 trang 50 SBT Toán 10 - Cánh Diều

Trong một trò chơi, bạn Hằng ghi tên 63 tỉnh, thành phố trực thuộc Trung ương của VN (tính đến năm 2021) vào 63 phiếu, hai phiếu khác nhau ghi tên hai nơi khác nhau, rồi bỏ tất cả các phiếu đó vào một hộp kín. Bạn Hoài rút ngẫu nhiên 2 phiếu. Tính xác suất của mỗi biến cố sau:

a) A: “Hai phiếu rút được ghi tên hai nơi bắt đầu bằng âm tiết Hà”

b) B: “Hai phiếu rút được ghi tên hai nơi bắt đầu bằng chữ K”

c) C: “Hai phiếu rút được ghi tên hai nơi bắt đầu bằng chữ B”

Lời giải:

Chọn 2 tỉnh thành trong số 63 tình thành \( \Rightarrow n\left( \Omega  \right) = C_{63}^2\)

a) A: “Hai phiếu rút được ghi tên hai nơi bắt đầu bằng âm tiết Hà”: có 4 tỉnh: HN, Hà Giang, Hà Tĩnh, Hà Nam \( \Rightarrow n\left( A \right) = C_4^2 = 6\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{6}{{C_{63}^2}} = \frac{2}{{651}}\)

b) B: “Hai phiếu rút được ghi tên hai nơi bắt đầu bằng chữ K”: có 3 tỉnh: Khánh Hòa, Kiên Giang, Kon Tum \( \Rightarrow n\left( B \right) = C_3^2 = 3\)

\( \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{3}{{C_{63}^2}} = \frac{1}{{651}}\)

 c) C: “Hai phiếu rút được ghi tên hai nơi bắt đầu bằng chữ B”: có 10 tỉnh: Bà Rịa – Vũng Tàu, Bắc Giang, Bắc Kạn, Bắc Ninh, Bạc Liêu, Bến Tre, Bình Phước, Bình Dương, Bình Định, Bình Thuận \( \Rightarrow n\left( C \right) = C_{10}^2 = 45\)

\( \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega  \right)}} = \frac{{45}}{{C_{63}^2}} = \frac{5}{{217}}\)

Bài 46 trang 50 SBT Toán 10 - Cánh Diều

Một đội thanh niên tình nguyện gồm 27 người đến từ các tỉnh (thành phố): Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng, Phú Yên, Khánh Hòa, Ninh Thuận, Bình Thuận, Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh, Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang và Cà Mau; mỗi tỉnh chỉ có đúng một thành viên của đội.

Chọn ngẫu nhiên 3 thành viên của đội để phân công nhiệm vụ trước. Tính xác suất của mỗi biến cố sau:

a) A: “Ba thành viên được chọn đến từ Tây Nguyên”

b) B: “Ba thành viên được chọn đến từ Duyên hải Nam Trung Bộ”

c) C: “Ba thành viên được chọn đến từ Đông Nam Bộ”

Lời giải:

Chọn 3 tỉnh thành trong số 27 tình thành \( \Rightarrow n\left( \Omega  \right) = C_{27}^3\)

a) A: “Ba thành viên được chọn đến từ Tây Nguyên”: có 5 tỉnh: Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng \( \Rightarrow n\left( A \right) = C_5^3 = 10\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{10}}{{C_{27}^3}} = \frac{2}{{585}}\)

b) B: “Ba thành viên được chọn đến từ Duyên hải Nam Trung Bộ”: có 4 tỉnh: Phú Yên, Khánh Hòa, Ninh Thuận, Bình Thuận \( \Rightarrow n\left( B \right) = C_4^3 = 4\)

\( \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{4}{{C_{27}^3}} = \frac{4}{{2925}}\)

c) C: “Ba thành viên được chọn đến từ Đông Nam Bộ”: có 5 tỉnh: Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh \( \Rightarrow n\left( C \right) = C_5^3 = 10\)

\( \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega  \right)}} = \frac{{10}}{{C_{27}^3}} = \frac{2}{{585}}\)

d) D: “Ba thành viên được chọn đến từ Đồng bằng sông Cửu Long”: có 13 tỉnh: Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang, Cà Mau \( \Rightarrow n\left( D \right) = C_{13}^3 = 286\)

\( \Rightarrow P\left( D \right) = \frac{{n\left( D \right)}}{{n\left( \Omega  \right)}} = \frac{{286}}{{C_{27}^3}} = \frac{{22}}{{225}}\)

Bài 47 trang 50 SBT Toán 10 - Cánh Diều

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ được rút ra và bỏ lại thẻ đó vào hộp. Xét phép thử “Rút ngẫu nhiên liên tiếp 3 chiếc thẻ trong hộp”.

Tính xác suất của biến cố A: “Tích các số ghi trên thẻ ở 3 lần rút là số chẵn”

Lời giải:

+ Rút 3 tấm thử liên tiếp trong 5 tấm thẻ \( \Rightarrow n\left( \Omega  \right) = 5.5.5 = 125\)

+ Xét biến cố đối \(\overline A \): “Tích các số ghi trên thẻ ở 3 lần rút là số lẻ” là biến cố đối của biến cố A \( \Rightarrow n\left( {\overline A } \right) = 3.3.3 = 27\)

\( \Rightarrow P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega  \right)}} = 1 - \frac{{27}}{{125}} = \frac{{98}}{{125}}\)

Bài 48 trang 50 SBT Toán 10 - Cánh Diều

Có 3 khách hàng (không quen biết nhau) cùng đến một cửa hàng có 5 quầy phục vụ khác nhau. Tính xác suất để có 2 khách hàng cùng vào 1 quầy và khách hàng còn lại vào quầy khác.

Lời giải:

+ Mỗi khách hàng có 5 cách chọn quầy \( \Rightarrow n\left( \Omega  \right) = 5.5.5 = 125\)

+ Gọi A là biến cố “2 khách hàng cùng vào 1 quầy và khách hàng còn lại vào quầy khác”

+ Số cách chọn 2 khách hàng là \(C_3^2 = 3\). Số cách chọn quầy cho 2 khách hàng đó là 5

+ Số cách chọn quầy cho khách hàng còn lại là 4 \( \Rightarrow n\left( A \right) = 3.5.4 = 60\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{60}}{{125}} = \frac{{12}}{{25}}\)

 Sachbaitap.com