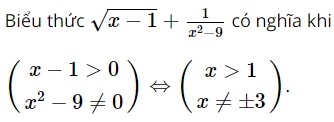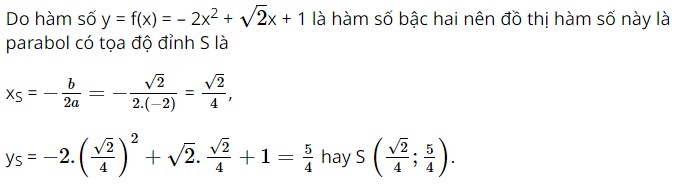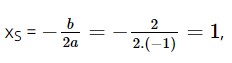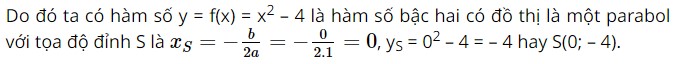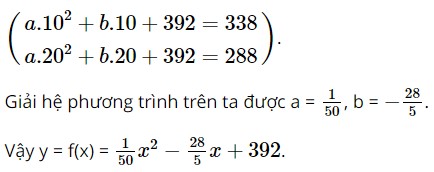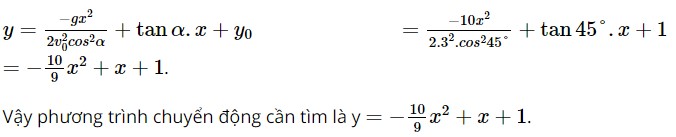Giải SBT Toán 10 trang 56, 57, 58 Chân trời sáng tạo tập 1

A. TRẮC NGHIỆM

Bài 1 trang 56 SBT Toán 10 - Chân trời sáng tạo

Một hàm số có thể được cho bằng:

A. Bảng giá trị của hàm số 

B. Đồ thị của hàm số

C. Công thức của hàm số 

D. Tất cả đều đúng

Lời giải:

Đáp án đúng là: D

Một hàm số có thể được cho bằng bảng giá trị của hàm số, hoặc bằng đồ thị của hàm số hoặc bằng công thức của hàm số. Vậy các đáp án A, B, C đều đúng, ta chọn đáp án D.

Bài 2 trang 56 SBT Toán 10 - Chân trời sáng tạo

Cho hàm số \(y = f\left( x \right) = 2\left( {x + 1} \right)\left( {x - 3} \right) + 2x - 6\). Giá trị của hàm số khi x=3 là:

A. 8 

B. 0

C. -6   

D. 3

Lời giải:

Đáp án đúng là: B

Thay x = 3 vào hàm số ta được:

f(3) = 2.(3 + 1).(3 – 3) + 2 . 3 – 6 = 0 + 6 – 6 = 0.

Vậy giá trị của hàm số khi x = 3 là 0.

Bài 3 trang 56 SBT Toán 10 - Chân trời sáng tạo

Hàm số \(y = f\left( x \right) = \sqrt {x - 1}  + \frac{1}{{{x^2} - 9}}\) có tập xác định là:

A. \(D = \left[ {1; + \infty } \right)\)

B. \(D = \mathbb{R}\backslash \left\{ { - 3;3} \right\}\)

C. \(D = \left[ {1; + \infty } \right)\backslash \left\{ 3 \right\}\)   

D. \(D = \left[ {3; + \infty } \right)\)

Lời giải:

Đáp án đúng là: C

Vậy tập xác định của hàm số là D = [1; + ∞) \ {3}.

Bài 4 trang 56 SBT Toán 10 - Chân trời sáng tạo

Hàm số nào trong các hàm số sau đây không phải là hàm số bậc hai?

A. \(y = f\left( x \right) = \sqrt 3 {x^2} + x - 4\)

B. \(y = f\left( x \right) = {x^2} + \frac{1}{x} - 5\)

C. \(y = f\left( x \right) =  - 2x\left( {x - 1} \right)\)

D. \(y = f\left( x \right) = 2\left( {{x^2} + 1} \right) + 3x - 1\)

Lời giải:

Đáp án đúng là: B

+) Hàm số y = f(x) = – 2x(x – 1) hay y = f(x) = – 2x² + 2x, đây là hàm số bậc hai do nó có dạng y = ax² + bx + c với a = – 2 ≠ 0, b = 2, c = 0.

+) Hàm số y = f(x) = 2(x² + 1) + 3x – 1 hay y = f(x) = 2x² + 3x + 1, đây hàm số bậc hai do nó có dạng y = ax² + bx + c với a = 2 ≠ 0, b = 3, c = 1.

Vậy trong các hàm số đã cho, chỉ có hàm số ở đáp án B không phải là hàm số bậc hai.

Bài 5 trang 57 SBT Toán 10 - Chân trời sáng tạo

Tập giá trị của hàm số \(y = f\left( x \right) =  - 2{x^2} + \sqrt 2 x + 1\) là:

A. \(T = \left( { - \frac{5}{4}; + \infty } \right)\)

B. \(T = \left[ { - \frac{5}{4}; + \infty } \right)\)

C. \(T = \left( { - \infty ;\frac{5}{4}} \right)\)   

D. \(T = \left( { - \infty ;\frac{5}{4}} \right]\)

Lời giải:

Đáp án đúng là: D

Lại có hàm số có hệ số a = – 2 < 0 nên bề lõm của parabol hướng xuống dưới, do đó đỉnh S là điểm cao nhất của đồ thị hàm số.

Bài 6 trang 57 SBT Toán 10 - Chân trời sáng tạo

Hàm số \(y = f\left( x \right) =  - \left( {x + 2} \right)\left( {x - 4} \right)\) đồng biến trên khoảng

A. \(\left( { - \infty ; - 1} \right)\)

B. \(\left( {1; + \infty } \right)\) 

C.  \(\left( { - \infty ;1} \right)\)

D. \(\left( { - 1; + \infty } \right)\)

Lời giải:

Đáp án đúng là: C

Ta có: – (x + 2)(x – 4) = – x² + 4x – 2x + 8 = – x² + 2x + 8.

Do đó ta có hàm số y = f(x) = – x² + 2x + 8.

Đây là hàm số bậc hai nên đồ thị hàm số là parabol với tọa độ đỉnh S là

yS = – 12 + 2 . 1 + 8 = 9 hay S(1; 9).

Do hệ số a = – 1 < 0 nên ta có bảng biến thiên:

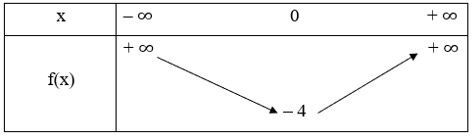
Vậy hàm số đã cho đồng biến trên khoảng (– ∞; 1).

Bài 7 trang 57 SBT Toán 10 - Chân trời sáng tạo

Hàm số \(y = f\left( x \right) = \left( {x + 2} \right)\left( {x - 2} \right)\) có:

A. Giá trị nhỏ nhất là 4 

B. Giá trị lớn nhất là 4

C. Giá trị lớn nhất là \( - 4\)

D. Giá trị nhỏ nhất là \( - 4\)

Lời giải:

Đáp án đúng là: D

Ta có: (x + 2)(x – 2) = x² – 4.

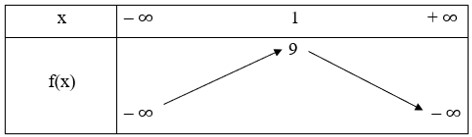
Vì hệ số a = 1 > 0 nên ta có bảng biến thiên

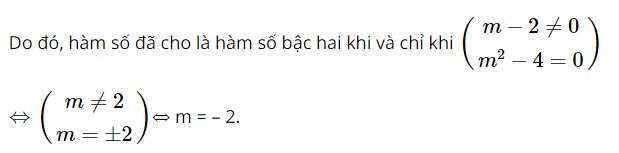
Từ bảng biến thiên, ta có giá trị nhỏ nhất của hàm số là – 4.

Bài 8 trang 57 SBT Toán 10 - Chân trời sáng tạo

Để hàm số \(y = f\left( x \right) = \left( {m - 2} \right){\left( {x + 5} \right)^2} + \left( {{m^2} - 4} \right)\left| {x - 7} \right| + 3\) là một hàm số bậc hai thì giá trị của m là:

A. \(2\)   

B. \(2\) hay \( - 2\) 

C. \( - 2\) 

D. \(4\)

Lời giải:

Đáp án đúng là: C

Ta có: y = f(x) = (m – 2)(x + 5)² + (m² – 4)|x – 7| + 3

⇔ y = f(x) = (m – 2)x² + 10(m – 2)x + 25(m – 2) + (m² – 4)|x – 7| + 3

Hàm số bậc hai có dạng y = ax² + bx + c với a ≠ 0 và không chứa dấu giá trị tuyệt đối.

Vậy m = – 2 thì thỏa mãn.

Bài 9 trang 57 SBT Toán 10 - Chân trời sáng tạo

Đồ thị hàm số \(y = f\left( x \right) =  - {x^2} + 4\left( {5m + 1} \right)x + \left( {3 - 2m} \right)\) có trục đối xứng là đường thẳng \(x =  - 2\) khi m có giá trị là:

A. \( - 3\)

B. \( - \frac{2}{5}\)

C. \(\frac{3}{2}\)

D. \( - \frac{1}{5}\)

Lời giải:

Đáp án đúng là: B

Hàm số y = f(x) = –x² + 4(5m + 1)x + (3 – 2m) là hàm số bậc hai.

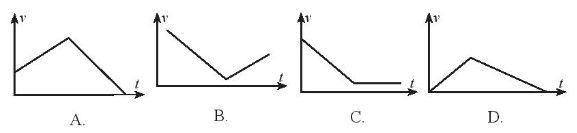
Bài 10 trang 57 SBT Toán 10 - Chân trời sáng tạo

Một viên bi được thả không vận tốc đầu và lăn trên máng nghiêng như hình 1

Đồ thị nào sau đây phù hợp với sự thay đổi vận tốc của viên bi theo thời gian?

Lời giải:

Đáp án đúng là: C

Quan sát Hình 1, ta thấy viên bi rơi từ trên cao xuống theo mặt phẳng nghiêng và tiếp tục lăn trên mặt phẳng ngang theo một đường thẳng. Do đó, trong các đồ thị ở trên, đồ thị ở đáp án C là phù hợp với sự thay đổi vận tốc của viên bi theo thời gian.

B. TỰ LUẬN

Bài 1 trang 58 SBT Toán 10 - Chân trời sáng tạo

Ta có bảng giá trị của hàm cầu đối với sản phẩm A theo đơn giá của sản phẩm A như sau:

a) Giả sử hàm cầu là một hàm số bậc hai theo đơn giá x , hãy viết công thức của hàm này, biết rằng \(c = 392\)

b) Chứng tỏ rằng hàm số có thể viết thành dạng \(y = f\left( x \right) = a{\left( {b - x} \right)^2}\)

c) Giả sử hàm cầu này lấy mọi giá trị trên đoạn \(\left[ {0;100} \right]\), hãy tính lượng cầu khi đơn giá sản phẩm A là 30, 50, 100

d) Cùng giả thiết với câu c) nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A là khoảng bao nhiêu (đơn vị: nghìn đồng)

Lời giải:

a) Theo giả thiết, hàm cầu là một hàm số bậc hai nên công thức của hàm số có dạng: y = f(x) = ax² + bx + 392 (a ≠ 0).

Ta chọn 2 cặp giá trị từ bảng đã cho lần lượt có x = 10, x = 20 thì được hệ phương trình sau:

Thep giả thiết câu c), hàm số xác định trên đoạn [0; 100] nên ta chọn x ≈ 53,4.

Vậy nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A khoảng 53 400 đồng.

Bài 2 trang 58 SBT Toán 10 - Chân trời sáng tạo

Khi một vật từ vị trí \({y_0}\) được ném xiên lên cao theo góc \(\alpha \) (so với phương ngang) với vận tốc ban đầu \({v_0}\) thì phương trình chuyển động của vật này là:

                 \(y = \frac{{ - g{x^2}}}{{2v_0^2{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}\)

a) Vật bị ném xiên như vậy có chuyển động theo đường xiên không? Tại sao?

b) Giả sử góc ném có số đo là \(45^\circ \), vận tốc ban đầu của vật là \(3\)m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, hãy viết phương trình chuyển động của vật

c) Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng \(45^\circ \). Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?

(Lưu ý: Lấy giá trị \(g = 10\) m/s² cho gia tốc trọng trường và làm tròn kết quả đến 2 chữ số thập phân)

Lời giải:

a) Với các giá trị đã biết là góc ném, vận tốc ban đầu và gia tốc trọng trường g là hằng số thì phương trình chuyển động trong ném xiên là một hàm số bậc hai theo x. Do vậy đồ thị của hàm số là một parabol. Quỹ đạo chuyển động của các vật cũng là một phần trên parabol này nên nó không thể chuyển động theo đường xiên.

b) Với góc ném có số đo là 45°, vận tốc ban đầu của vật là 3 m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, ta có phương trình chuyển động của vật này là:

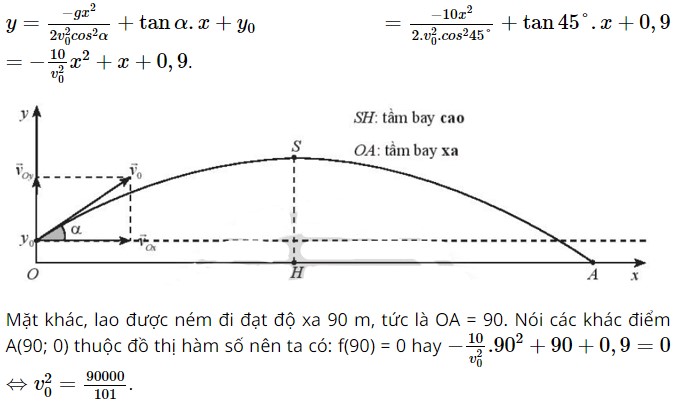
c) Theo giả thiết bài toán, ta có phương trình chuyển động của lao sau khi ném là:

Suy ra v0 ≈ 29,85 (m/s).

Vậy vận tốc đầu của lao khi được ném đi xấp xỉ bằng 29,85 m/s.

Sachbaitap.com