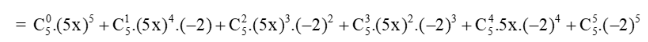Giải SBT Toán 10 trang 57 Kết nối tri thức tập 2Bài 8.13, 8.14. 8.15, 8.16, 8.17 trang 57 SBT Toán 10 KNTT tập 2. Khai triển các đa thức. Hãy sử dụng ba số hạng đầu tiên trong khai triển của (1 + 0.03) ^ 4 để tính giá trị gần đúng của 1,03 ^ 4. Xác định sai số tuyệt đối. Bài 8.13 trang 57 SBT Toán 10 tập 2 Kết nối tri thức Khai triển các đa thức a) \({(x - 2)^4}\); b) \({(x + 2)^5}\); c) \({(2x - 3y)^4}\); d) \({(2x - y)^5}\). Lời giải: a) \({(x - 2)^4} = {x^4} + 4{x^3}( - 2) + 6{x^2}{( - 2)^2} + 4x{( - 2)^3} + {( - 2)^4}\) \( = {x^4} - 8{x^3} + 24{x^2} - 32x + 16\) b) \({(x + 2)^5} = {x^5} + 5{x^4}.2 + 10{x^3}{.2^2} + 10{x^2}{.2^3} + 5x{.2^4} + {2^5}\) \( = {x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\) c) \({(2x - 3y)^4} = {(2x)^4} + 4{(2x)^3}(3y) + 6{(2x)^2}{(3y)^2} + 4(2x){(3y)^3} + {(3y)^4}\) \( = 16{x^4} + 96{x^3}y + 216{x^2}{y^2} + 216x{y^3} + 81{y^4}\) d) \({(2x - y)^5} = {(2x)^5} + 5{(2x)^4}.( - y) + 10{(2x)^3}.{( - y)^2}\) \( + 10{(2x)^2}.{( - y)^3} + 5(2x).{( - y)^4} + {( - y)^5}\) \( = 32{x^5} - 80{x^4}y + 80{x^3}{y^2} - 40{x^2}{y^3} + 10x{y^4} + 32{y^5}\) Bài 8.14 trang 57 SBT Toán 10 tập 2 Kết nối tri thức Trong khai triển của \({(5x - 2)^5}\), số mũ của x được sắp xếp theo lũy thừa tăng dần, hãy tìm hạng tử thứ hai. Lời giải: Áp dụng công thức khai triển của (a + b)5 với a = 5x, b = –2, ta có: (5x – 2)5 = 1 . 3 125x5 + 5 . 625x4.(–2) + 10 . 125x3.4 + 10 . 25x2.(–8) + 5 . 5x.16 + 1.(–32) = 3 125x5 – 6 250x4 + 5 000x3 – 2 000x2 + 400x – 32 = – 32 + 400x – 2 000x2 + 5 000x3 – 6 250x4 + 3 125x5 Vậy, số hạng thứ hai trong khai triển theo số mũ tăng dần của x là 400x. Bài 8.15 trang 57 SBT Toán 10 tập 2 Kết nối tri thức Hãy sử dụng ba số hạng đầu tiên trong khai triển của \({(1 + 0,03)^4}\) để tính giá trị gần đúng của \(1,{03^4}\). Xác định sai số tuyệt đối. Lời giải: Ta có: 1,034 = (1 + 0,03)4 = 14 + 4.13.0,03 + 6.12.(0,03)2 + … = 1 + 0,12 + 0,0054 + … ≈ 1,1254 Mặt khác, ta tính được giá trị đúng, chẳng hạn bằng máy tính, 1,034 = 1,12550881. Như vậy, sai số tuyệt đối của của giá trị gần đúng nhận được so với giá trị đúng là: |1,1254 – 1,12550881| = 0,00010881. Bài 8.16 trang 57 SBT Toán 10 tập 2 Kết nối tri thức Xác định hạng tử không chứa x trong khai triển của \({\left( {x + \frac{2}{x}} \right)^4}\). Lời giải: Ta có: \(\begin{array}{l}{\left( {x + \frac{2}{x}} \right)^4} = {x^4} + 4{x^3}\frac{2}{x} + 6{x^2}{\left( {\frac{2}{x}} \right)^2} + 4x{\left( {\frac{2}{x}} \right)^3} + {\left( {\frac{2}{x}} \right)^4}\\ = {x^4} + 8{x^2} + 24 + \frac{{32}}{{{x^2}}} + \frac{{16}}{{{x^4}}}\end{array}\) Vậy hạng tử không chứa x là 24. Bài 8.17 trang 57 SBT Toán 10 tập 2 Kết nối tri thức Khai triển \({\left( {{z^2} + 1 + \frac{1}{z}} \right)^4}\) Lời giải: Ta có: \({\left( {{z^2} + 1 + \frac{1}{z}} \right)^4}\) \( = {({z^2} + 1)^4} + 4{({z^2} + 1)^3}\frac{1}{z} + 6{({z^2} + 1)^2}{\left( {\frac{1}{z}} \right)^2} + 4({z^2} + 1){\left( {\frac{1}{z}} \right)^3} + {\left( {\frac{1}{z}} \right)^4}\) \(\begin{array}{l} = ({z^8} + 4{z^6} + 6{z^4} + 4{z^2} + 1) + 4.({z^6} + 3{z^4} + 3{z^2} + 1)\left( {\frac{1}{z}} \right)\\ + 6({z^4} + 2{z^2} + 1)\left( {\frac{1}{{{z^2}}}} \right) + 4({z^2} + 1)\left( {\frac{1}{{{z^3}}}} \right) + \left( {\frac{1}{{{z^4}}}} \right)\end{array}\) \( = {z^8} + 4{z^6} + 4{z^5} + 12{z^3} + 10{z^2} + 12z + 13 + \frac{8}{z} + \frac{6}{{{z^2}}} + \frac{4}{{{z^3}}} + \frac{1}{{{z^4}}}\) Sachbaitap.com
Xem thêm tại đây:
Bài 25. Nhị thức Newton
|
-

Giải SBT Toán 10 trang 58, 59, 60 Kết nối tri thức tập 2
Bài 8.18, 8.19, 8.20, 8.21, 8.22, 8.23, 8.24 trang 58, bài 8.25, 8.26, 8.27, 8.28, 8.29, 8.30, 8.31, 8.32 trang 59, bài 8.33, 8.34, 8.35, 8.36, 8.37 trang 60 SBT Toán 10 KNTT tập 2. Tại một cuộc họp của học sinh các lớp 10A, 10BB, 10C, 10D và 10E, ban tổ chức đề nghị đại diện của mỗi lớp trình bày một báo cáo. Ban đại diện của lớp 10A đề nghị được trình bày báo cáo ngay trước đại diện của lớp 10B và được ban tổ chức đồng ý. Số cách xếp chương trình là

 Tải ngay
Tải ngay