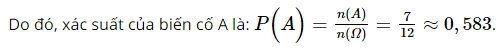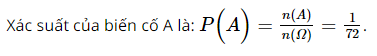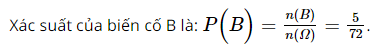Giải SBT Toán 10 trang 63 Kết nối tri thức tập 2

Bài 9.1 trang 63 SBT Toán 10 tập 2 Kết nối tri thức

Gieo một con xúc xắc liên tiếp hai lần.

a) Mô tả không gian mẫu. 

b) Gọi A là biến cố: “Tổng số chấm xuất hiện lớn hơn hay bằng 8". Biến cố A và \(\overline A \) là các tập con nào của không gian mẫu?

Lời giải:

a) Không gian mẫu là tập hợp các cặp số (x;y) thỏa mãn: \(x,y \in \left\{ {1;2;3;4;5;6} \right\}\)

\(\Omega  = {\rm{ }}\left\{ {\left( {x,y} \right){\rm{| x,y}} \in {\rm{N; }}1 \le x,y \le 6} \right\}\)

b)

+ Biến cố A là tập hợp các cặp số (x;y) thỏa mãn: \(x + y \ge 8\)

A = {(2,6); (3,5); (3, 6); (4, 4); (4, 5); (4, 6); (5, 3); (5, 4); (5, 5); (5, 6); (6, 2); (6, 3); (6, 4); (6,5); (6, 6)}.

 + Biến cố \(\overline A \) là tập hợp các cặp số (x;y) thỏa mãn: \(x + y < 8\)

\(\overline A =\{(1,1);(1,2);(1,3);(1,4);(1,5);\)\((1,6);(2,1);(2,2);(2,3);(2,4);(2,5);\)\((3,1);(3,2);(3,3);(3,4);(4,1);(4,2);(4,3);(5,1);(5,2);(6,1)\} \)

Bài 9.2 trang 63 SBT Toán 10 tập 2 Kết nối tri thức

Gieo một con xúc xắc đồng thời rút ngẫu nhiên một thẻ từ một hộp chứa 4 thẻ A, B, C, D.

a) Mô tả không gian mẫu.

b) Xét các biến cố sau:

E: “Con xúc xắc xuất hiện mặt 6";

\(F\) : “Rút được thẻ A hoặc con xúc xắc xuất hiện mặt 5".

Các biến cố \(E,\,\overline E ,F \) và \(\overline F \) là các tập con nào của không gian mẫu?

Lời giải:

a) Không gian mẫu là:

\(\Omega  = \{ (1,A);(2,A);(3,A);(4,A);\)\((5,A);(6,A);(1,B);(2,B);(3,B);\)\((4,B);(5,B);(6,B);(1,C);(2,C);\)\((3,C);(4,C);(5,C);(6,C);(1,D);\)\((2,D);(3,D);(4,D);(5,D);(6,D)\} \)

b) Tập hợp E là: E = {(6, A); (6, B); (6, C); (6, D)}.

Tập hợp \(\overline E \) là: \(\overline E \)  = {(1, A); (2, A); (3, A); (4, A); (5, A); (1, B): (2, B); (3, B); (4, B); (5, B); (1, C); (2, C); (3, C); (4, C); (5, C); (1, D); (2, D); (3, D); (4, D); (5, D)}.

Tập hợp F là: F = {(5, A); (5, B); (5, C); (5, D); (1, A); (2. A); (3, A); (4, A); (6, A)}.

Tập hợp \(\overline F \) là: \(\overline F \) = {(1, B); (2, B); (3, B); (4, B); (6, B); (1, C); (2, C); (3, C); (4, C); (6, C); (1, D); (2, D); (3, D); (4, D); (6, D)}.

Bài 9.3 trang 63 SBT Toán 10 tập 2 Kết nối tri thức

Hai túi I và II chứa các tấm thẻ được đánh số. Túi I: {1; 2; 3; 4;}, túi II: {1; 2; 3; 4; 5}. Rút ngẫu nhiên từ mỗi túi I và II một tấm thẻ.

a) Mô tả không gian mẫu.

b) Xét các biến cố sau:

A: “Hai số trên hai tấm thẻ bằng nhau";

B: “Hai số trên hai tấm thẻ chênh nhau 2";

C: “Hai số trên hai tấm thẻ chênh nhau lớn hơn hay bằng 2".

Các biến cố \(A,\overline A ,B,\overline B ,C,\overline C \)là các tập con nào của không gian mẫu?

Lời giải:

a) Không gian mẫu là: \(\Omega \)  = {(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (2, 1); (2, 2), (2, 3); (2, 4); (2,5); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (4, 1); (4, 2); (4,3); (4, 4); (4, 5)}.

b) Tập hợp A là: A = {(1,1); (2, 2); (3, 3); (4,4)}.

Tập hợp \(\overline A \) là: \(\overline A \) = {(1, 2); (1, 3); (1, 4); (1, 5); (2, 1); (2, 3); (2, 4); (2, 5); (3, 1); (3, 2); (3, 4); (3, 5); (4, 1); (4, 2); (4, 3); (4,5)}.

Tập hợp B là: B = {(1,3); (3, 1); (2, 4); (4, 2); (3,5)}.

Tập hợp \(\overline B \) là: \(\overline B \) = {(1, 1); (1, 2); (1, 4); (1, 5); (2, 1); (2, 2); (2, 3); (2, 5); (3, 2); (3, 3); (3, 4); (4, 1); (4, 3); (4, 4); (4,5)}.

Tập hợp C là: C = {(1, 3); (1, 4); (1, 5); (2, 4); (2, 5); (3, 1); (3,5); (4, 1); (4, 2)}

Tập hợp \(\overline C \)là: \(\overline C \)= {(1, 1); (1, 2); (2, 1); (2, 2); (2, 3); (3, 2); (3, 3); (3, 4); (4, 3); (4, 4); (4,5)}

Bài 9.4 trang 63 SBT Toán 10 tập 2 Kết nối tri thức

Gieo một đồng xu và một con xúc xắc đồng thời. Tính xác suất của biến cố A: “Đồng xu xuất hiện mặt sấp hoặc con xúc xắc xuất hiện mặt 5 chấm”.

Lời giải:

Gieo một đồng xu 1 lần ta thu được kết quả bất kì thuộc tập hợp: {sấp; ngửa}.

Gieo một con xúc xắc 1 lần ta thu được kết quả bất kì thuộc tập hợp: {1; 2; 3; 4; 5; 6}.

Do đó, không gian mẫu là:

Ω = {(sấp, 1); (sấp, 2); (sấp, 3); (sấp, 4); (sấp, 5); (sấp, 6); (ngửa, 1); (ngửa, 2); (ngửa, 3); (ngửa, 4); (ngửa, 5); (ngửa, 6)}.

Số phần tử của Ω là: n(Ω) = 12.

Xét biến cố A: “Đồng xu xuất hiện mặt sấp hoặc con xúc xắc xuất hiện mặt 5 chấm”.

A₁: “Đồng xu xuất hiện mặt sấp”. Ta có: A₁ = {(sấp, 1); (sấp, 2); (sấp, 3); (sấp, 4); (sấp, 5); (sấp, 6)}.

A₂: “Con xúc xắc xuất hiện mặt 5 chấm”. Ta có: A₂ = {(sấp, 5); (ngửa, 5)}.

Do đó, ta có:

A = A₁ ∪ A₂ = {(ngửa, 5); (sấp, 1); (sấp, 2); (sấp, 3); (sấp, 4); (sấp, 5); (sấp, 6)}.

Số phần tử của A là: n(A) = 7.

Bài 9.5 trang 63 SBT Toán 10 tập 2 Kết nối tri thức

Có hai hộp I và II. Hộp thứ nhất chứa 12 tấm thẻ vàng đánh số từ 1 đến 12. Hộp thứ hai chứa 6 tấm thẻ đỏ đánh số từ 1 đến 6. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Tính xác suất của các biến cố:

a) A: “Cả hai tấm thẻ đều mang số 5".

b) B: “Tổng hai số trên hai tấm thẻ bằng 6”.

Lời giải:

Rút ngẫu nhiên từ hộp I một tấm thẻ ta nhận được tấm thẻ vàng đánh số a bất kì với 1 ≤ a ≤ 12, a ∈ ℕ.

Rút ngẫu nhiên từ hộp II một tấm thẻ ta nhận được tấm thẻ đỏ đánh số b bất kì với 1 ≤ b ≤ 6, b ∈ ℕ.

Do đó, không gian mẫu là:

Ω = {(a, b), 1 ≤ a ≤ 12, 1 ≤ b ≤ 6, a, b ∈ ℕ}.

Do đó theo quy tắc nhân, Ω có: 12 . 6 = 72 (phần tử) hay n(Ω) = 72.

a)

Xét biến cố A: “Cả hai tấm thẻ đều mang số 5”. Ta có:

Khi a = 5 thì b = 5

Do đó A = {(5, 5)}.

 Số phần tử của A là: n(A) = 1 .

b)

Xét biến cố B: “Tổng hai số trên hai tấm thẻ bằng 6”. Ta có:

Khi a = 1 thì b = 5

Khi a = 2 thì b = 4

Khi a = 3 thì b = 3

Khi a = 4 thì b = 2

Khi a = 5 thì b = 1

Khi a ≥ 6 thì không tồn tại b với 1 ≤ b ≤ 6 thỏa mãn

Do đó B = {(1, 5); (2, 4); (3, 3); (4, 2); (5, 1)}.

Số phần tử của B là: n(B) = 5.

Bài 9.6 trang 63 SBT Toán 10 tập 2 Kết nối tri thức

Có ba chiếc hộp. Hộp thứ nhất chứa 5 tấm thẻ đánh số từ 1 đến 5. Hộp thứ hai chứa 6 tấm thẻ đánh số từ 1 đến 6. Hộp thứ ba chứa 7 tấm thẻ đánh số từ 1 đến 7. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ. Tính xác suất để tống ba số ghi trên ba tấm thẻ bằng 15.

Lời giải:

Ta có không gian mẫu là: \(\Omega  = \left\{ {\left( {a,b,c} \right),1 \le a \le 5;1 \le b \le 6;1 \le c \le 7} \right\}\). Vậy n(\(\Omega \)) =5.6.7 = 210.

Gọi A là biến cố “tống ba số ghi trên ba tấm thẻ bằng 15”.

Khi đó A = {(2, 6, 7); (3, 6, 6); (3, 5, 7); (4, 6, 5); (4, 5, 6); (4, 4, 7); (5, 3, 7); (5, 4, 6); (5, 5, 5); (5, 6, 4)}. Vậy n(A) = 10.

Do đó P(A) = \(\frac{{10}}{{210}} = \frac{1}{{21}}\).

Sachbaitap.com