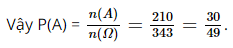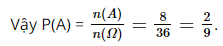Giải SBT Toán 10 trang 67, 68, 69 Kết nối tri thức tập 2Bài 9.13, 9.14, 9.15, 9.16 trang 67, bài 9.17, 9.18, 9.19, 9.20, 9.21, 9.22, 9.23 trang 68, bài 9.24, 9.25, 9.26, 9.27, 9.28 trang 69 SBT Toán 10 KNTT tập 2. Gieo ba con xúc xắc cân đối. Tính xác suất để tổng số chấm xuất hiện trên ba con xúc xắc bằng 7. Một chiếc hộp đựng 6 quả cầu trắng, 4 quả cầu đỏ và 2 quả cầu đen. Chọn ngẫu nhiên 6 quả cầu. Tính xác suất để chọn được 3 quả trắng, 2 quả đỏ và 1 quả đen. Bài 9.13 trang 67 SBT Toán 10 tập 2 Kết nối tri thức Xếp ngẫu nhiên ba bạn An, Bình, Cường đứng trên một hàng dọc. a) Xác suất để An không đứng cuối hàng là: A. \(\frac{2}{3}\). B. \(\frac{1}{3}\). C.\(\frac{3}{5}\). D.\(\frac{2}{5}\). b) Xác suất để Bình và Cường đứng cạnh nhau là A. \(\frac{1}{4}\). B. \(\frac{2}{3}\). C. \(\frac{2}{5}\). D.\(\frac{1}{2}\). c) Xác suất để An đứng giữa Bình và Cường là A. \(\frac{2}{3}\). B. \(\frac{1}{3}\). C.\(\frac{3}{5}\). D.\(\frac{2}{5}\). d) Xác suất để Bình đứng trước An là A. \(\frac{1}{4}\). B. \(\frac{2}{3}\). C. \(\frac{2}{5}\). D.\(\frac{1}{2}\). Lời giải: Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 3! = 6\). a) Gọi X là biến cố “An không đứng cuối hàng”. Khi đó ta có \(X = \left\{ {\left( {A,B,C} \right),\left( {A,C,B} \right),\left( {B,A,C} \right),\left( {C,A,B} \right)} \right\}\). Suy ra \(n\left( X \right) = 4\). Vậy \(P\left( X \right) = \frac{{n\left( X \right)}}{{n\left( \Omega \right)}} = \frac{2}{3}\). Chọn A b) Gọi Y là biến cố “Bình và Cường đứng cạnh nhau”. Khi đó ta có \(Y = \left\{ {\left( {A,B,C} \right),\left( {A,C,B} \right),\left( {B,C,A} \right),\left( {C,B,A} \right)} \right\}\). Suy ra \(n\left( Y \right) = 4\). Vậy \(P\left( Y \right) = \frac{{n\left( Y \right)}}{{n\left( \Omega \right)}} = \frac{2}{3}\). Chọn B c) Gọi Z là biến cố “An đứng giữa Bình và Cường”. Khi đó ta có \(Z = \left\{ {\left( {B,A,C} \right),\left( {C,A,B} \right)} \right\}\). Suy ra \(n\left( Z \right) = 2\). Vậy \(P\left( Z \right) = \frac{{n\left( Z \right)}}{{n\left( \Omega \right)}} = \frac{1}{3}\) Chọn B d) Gọi T là biến cố “Bình đứng trước An”. Khi đó ta có \(T = \left\{ {\left( {B,A,C} \right),\left( {B,C,A} \right),\left( {C,B,A} \right)} \right\}\). Suy ra \(n\left( T \right) = 3\). Vậy \(P\left( T \right) = \frac{{n\left( T \right)}}{{n\left( \Omega \right)}} = \frac{1}{2}\) Chọn D Bài 9.14 trang 67 SBT Toán 10 tập 2 Kết nối tri thức Một cái túi đựng 3 viên bi đỏ, 5 viên bi xanh và 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Xác suất để chọn được 3 viên bi màu đỏ là: A. \(\frac{1}{{364}}\). B. \(\frac{1}{{14}}\). C. \(\frac{1}{{182}}\). D.\(\frac{1}{{95}}\). Lời giải: Có tất cả 3+5+6=14 viên bi Vậy có \(n\left( \Omega \right) = C_{14}^3 = 364\) cách lấy ra 3 viên bi bất kì Gọi A là biến cố “Chọn được 3 viên bi màu đỏ”. Khi đó số cách chọn 3 viên bi màu đỏ là \(C_3^3\) . Do đó \(n\left( A \right) = C_3^3 = 1\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{{364}}\). Chọn A Bài 9.15 trang 67 SBT Toán 10 tập 2 Kết nối tri thức Gieo hai con xúc xắc cân đối. a) Xác suất để có đúng 1 con xúc xắc xuất hiện mặt 6 chấm là: A. \(\frac{{11}}{{36}}\). B. \(\frac{1}{3}\). C. \(\frac{5}{{18}}\). D.\(\frac{4}{9}\). b) Xác suất để tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 7 là: A. \(\frac{{11}}{{36}}\). B. \(\frac{7}{{12}}\). C. \(\frac{5}{{11}}\). D.\(\frac{4}{9}\). Lời giải: Ta có \(n\left( \Omega \right) = 6.6 = 36\). a) Gọi A là biến cố “có đúng một con xúc xắc xuất hiện mặt 6 chấm”. Thực hiện hai công đoạn: + Chọn một trong hai con xúc xắc xuất hiện mặt 6 chấm: có 2 cách + Xúc xắc còn lại có 5 cách xuất hiện số chấm (trừ mặt 6 chấm). Suy ra \(n\left( A \right) = 2.5 = 10\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{10}}{{36}} = \frac{5}{{18}}\) Chọn C b) Gọi A là biến cố “tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 7”. Số chấm xuất hiện trên 2 xúc xắc có thể là \(\begin{array}{l}\left( {1;1} \right),\left( {1;2} \right),\left( {1;3} \right),\left( {1;4} \right),\left( {1;5} \right),\left( {1;6} \right),\\\left( {2;1} \right),\left( {2;2} \right),\left( {2;3} \right),\left( {2;4} \right),\left( {2;5} \right),\\\left( {3;1} \right),\left( {3;2} \right),\left( {3;3} \right),\left( {3;4} \right),\\\left( {4;1} \right),\left( {4;2} \right),\left( {4;3} \right),\\\left( {5;1} \right),\left( {5;2} \right),\\\left( {6;1} \right)\end{array}\) Suy ra \(n\left( A \right) = 6 + 5 + 4 + 3 + 2 + 1 = 21\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{21}}{{36}} = \frac{7}{{12}}\). Chọn B Bài 9.16 trang 67 SBT Toán 10 tập 2 Kết nối tri thức Chọn ngẫu nhiên 5 số trong tập S = {1; 2; ...; 20}. Xác suất để cả 5 số được chọn không vượt quá 10 xấp xỉ là: A. \(0,016\). B. \(0,013\). C. \(0,014\). D.\(0,015\). Lời giải: Ta có \(n\left( \Omega \right) = C_{20}^5\). Gọi A là biến cố đang xét. Khi đó số cách chọn 5 số từ tập \(\left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\)là \(C_{10}^5\). Suy ra \(n\left( A \right) = C_{10}^5\). Vậy \(P\left( A \right) = \frac{{C_{10}^5}}{{C_{20}^5}} \approx 0,016\). Chọn A Bài 9.17 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Chọn ngẫu nhiên 5 học sinh trong một danh sách được đánh số thứ tự từ 1 đến 199. a) Xác suất để cả 5 học sinh được chọn có số thứ tự nhỏ hơn 100 xấp xỉ là A. 0,028. B. 0,029. C. 0,027. D.0,026. b) Xác suất để cả 5 học sinh được chọn Có số thứ tự lớn hơn 149 xấp xỉ là A. 0,00089. B. 0,00083. C. 0,00088. D. 0,00086. Lời giải: Ta có \(n\left( \Omega \right) = C_{199}^5\). a) Gọi A là biến cố đang xét. Khi đó, số cách chọn 5 học sinh có số thứ tự nhỏ hơn 100 là \(C_{99}^5\). Suy ra \(n\left( A \right) = C_{99}^5\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{99}^5}}{{C_{199}^5}} \approx 0,029\) Chọn B b) Gọi A là biến cố đang xét. Khi đó, số cách chọn 5 học sinh có số thứ tự lớn hơn 149 là \(C_{50}^5\). Suy ra \(n\left( A \right) = C_{50}^5\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{51}^5}}{{C_{199}^5}} \approx 0,00086\) Chọn D Bài 9.18 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Một túi đựng 3 viên bị trắng và 5 viên bị đen. Chọn ngẫu nhiên 3 viên bi. Xác suất để trong 3 viên bị đó có cả bi trắng và bị đen là A. \(\frac{{13}}{{15}}\). B. \(\frac{9}{{11}}\). C. \(\frac{{43}}{{56}}\). D.\(\frac{{45}}{{56}}\). Lời giải: Ta có \(n\left( \Omega \right) = C_8^3\). Gọi A là biến cố “chọn ngẫu nhiên được 3 viên bi có cả bi trắng và đen”. Suy ra \(\overline A \) là biến cố “chọn ngẫu nhiên được 3 viên bi chỉ có màu trắng hoặc màu đen”. Khi đó \(n\left( {\overline A } \right) = C_3^3 + C_5^3 = 11\). Suy ra \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{11}}{{C_8^3}} = \frac{{11}}{{56}}\). Vậy \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = 1 - \frac{{11}}{{56}} = \frac{{45}}{{56}}\). Chọn D Bài 9.19 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Mũi tên của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong 7 vị trí. Người chơi được quay 3 lần. Xác suất để mũi tên dừng lại ở ba vị trí khác nhau là A. \(\frac{{30}}{{49}}\). B. \(\frac{{29}}{{50}}\). C. \(\frac{3}{5}\). D.\(\frac{7}{{11}}\) Lời giải: Đáp án đúng là: A Quay ngẫu nhiên 3 lần, mỗi lần có thể dừng lại ở một trong 7 vị trí. Do đó, n(Ω) = 7 . 7 . 7 = 343. Gọi biến cố A: “mũi tên dừng lại ở ba vị trí khác nhau trong 3 lần quay”. Lần quay thứ nhất có số cách chọn vị trí là: 7 Lần quay thứ hai có số cách chọn vị trí là: 6 Lần quay thứ ba có số cách chọn vị trí là: 5 Số cách để mũi tên dừng lại ở ba vị trí khác nhau là: 7 . 6 . 5 = 210 (cách) Do đó, n(A) = 210. Bài 9.20 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Gieo đồng thời hai con xúc xắc cân đối. Xác suất để số chấm xuất hiện trên hai con xúc xắc hơn kém nhau 2 là: A. \(\frac{5}{{22}}\). B. \(\frac{1}{5}\). C. \(\frac{2}{9}\). D.\(\frac{7}{{34}}\). Lời giải: Đáp án đúng là: C Không gian mẫu là: Ω = {(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6); (4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)}. Suy ra n(Ω) = 36. Biến cố A: “số chấm xuất hiện trên hai con xúc xắc hơn kém nhau 2”. A = (1, 3); (2, 4); (3, 5); (4, 2); (5, 3); (6, 4); (3, 1); (4, 6)}. Suy ra n(A) = 8. Bài 9.21 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Chọn ngẫu nhiên hai số từ tập hợp S = {1; 2; ... 19} rồi nhân hai số đó với nhau. Xác suất để kết quả là một số lẻ là: A. \(\frac{9}{{19}}\). B. \(\frac{{10}}{{19}}\). C. \(\frac{4}{{19}}\). D.\(\frac{5}{{19}}\). Lời giải: Ta có \(n\left( \Omega \right) = C_{19}^2\). Gọi A là biến cố “2 số chọn ra có tích là một số lẻ”. Để tích của hai số là một số lẻ thì 2 số đó đều phải là số lẻ. Vậy hai số chọn ra phải thuộc tập \(X = \left\{ {1;3;5;...;19} \right\}\). Suy ra \(n\left( A \right) = C_{10}^2\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{19}^2}} = \frac{5}{{19}}\) Chọn D Bài 9.22 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Gieo ba con xúc xắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên mặt của ba con xúc xắc khác nhau là A. \(\frac{5}{9}\). B. \(\frac{4}{9}\). C. \(\frac{7}{9}\). D.\(\frac{2}{9}\). Lời giải: Ta có \(n\left( \Omega \right) = 6.6.6 = 216\). Gọi A là biến cố “số chấm xuất hiện trên mặt của ba con xúc xắc khác nhau”. Khi đó \(n\left( A \right) = A_6^3\).Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{9}\) Chọn A Bài 9.23 trang 68 SBT Toán 10 tập 2 Kết nối tri thức Một khách sạn có 6 phòng đơn. Có 10 khách thuê phòng trong đó có 6 nam và 4 nữ. Người quản lí chọn ngẫu nhiên 6 người cho nhận phòng. a) Xác suất để cả 6 người là nam là: A. \(\frac{{11}}{{210}}\). B. \(\frac{1}{{105}}\). C. \(\frac{1}{{210}}\). D.\(\frac{7}{{210}}\). b) Xác suất để có 4 nam và 2 nữ là: A. \(\frac{2}{7}\). B. \(\frac{3}{7}\). C. \(\frac{4}{7}\). D.\(\frac{5}{7}\). c) Xác suất để có ít nhất 3 nữ là: A. \(\frac{2}{7}\). B. \(\frac{3}{7}\). C. \(\frac{4}{7}\). D.\(\frac{5}{7}\). Lời giải: Ta có \(n\left( \Omega \right) = C_{10}^6\). a) Gọi A là biến cố “chọn được 6 người đều là nam”. Suy ra \(n\left( A \right) = C_6^6 = 1\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{{C_{10}^6}} = \frac{1}{{210}}\) Chọn C b) Gọi B là biến cố “chọn được 4 nam và 2 nữ”. Suy ra \(n\left( B \right) = C_6^4.C_4^2 = 90\) Vậy \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{90}}{{C_{10}^6}} = \frac{3}{7}\) Chọn B c) Gọi C là biến cố “chọn được ít nhất 3 nữ”. + Chọn 3 nữ và 3 nam: Có \(C_4^3.C_6^3\) cách + Chọn 4 nữ và 2 nam: Có \(C_4^4.C_6^2\) cách Suy ra \(n\left( C \right) = C_4^3.C_6^3 + C_4^4.C_6^2 = 95\) Vậy \(P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{95}}{{C_{10}^6}} = \frac{{19}}{{42}}\) Chọn D Bài 9.24 trang 69 SBT Toán 10 tập 2 Kết nối tri thức Gieo ba con xúc xắc cân đối. Tính xác suất để tổng số chấm xuất hiện trên ba con xúc xắc bằng 7. Lời giải: Mỗi xúc xắc có 6 cách xuất hiện số chấm do đó \(n\left( \Omega \right) = 6.6.6 = 216\). Gọi A là biến cố “tổng số chấm xuất hiện trên ba con xúc xắc bằng 7”. Chỉ các bộ số \(\left( {1,1,5} \right);\left( {1,2,4} \right) & ;\left( {1,3,3} \right);\left( {2,2,3} \right)\) có tổng bằng 7 Các bộ số \(\left( {1,1,5} \right);\left( {1,3,3} \right);\left( {2,2,3} \right)\) mỗi bộ có 3 hoán vị và bộ số \(\left( {1,2,4} \right)\) có 6 hoán vị nên suy ra \(n\left( A \right) = 3.3 + 6 = 15\). Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{15}}{{216}} = \frac{5}{{72}}\) Bài 9.25 trang 69 SBT Toán 10 tập 2 Kết nối tri thức Một cửa hàng bán ba loại kem: xoài, sô cô la và sữa. Một học sinh chọn mua ba cốc kem một cách ngẫu nhiên. Tính xác suất để ba cốc kem chọn được thuộc hai loại. Phương pháp: Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\). Lời giải: Kí hiệu A là kem xoài, B là kem sô cô la và C là kem sữa. Suy ra \(\Omega = {\rm{ }}\{ AAA;{\rm{ }}BBB;{\rm{ }}CCC;{\rm{ }}ABC;{\rm{ }}ABB;{\rm{ }}ACC;{\rm{ }}BCC;{\rm{ }}BAA;{\rm{ }}CAA;{\rm{ }}CBB\} \). Do đó n(\(\Omega \)) = 10. Gọi E là biến cố: “Ba cốc kem chọn thuộc hai loại". Khi đó\(E{\rm{ }} = {\rm{ }}\{ ABB;{\rm{ }}ACC;{\rm{ }}BCC;{\rm{ }}BAA;{\rm{ }}CAA;{\rm{ }}CBB\} \). Suy ra n(E) = 6. Vậy\(P\left( E \right) = \frac{6}{{10}}{\rm{ = }}0,6\). Bài 9.26 trang 69 SBT Toán 10 tập 2 Kết nối tri thức Hai thầy trò đến dự một buổi hội thảo. Ban tổ chức xếp ngẫu nhiên 6 đại biểu trong đó có hai thầy trò ngồi trên một chiếc ghế dài. Tính xác suất đề hai thầy trò ngồi cạnh nhau. Phương pháp: Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\). Lời giải: Ta có \(n\left( \Omega \right) = 6! = 720\). Gọi E là biến cố: “Hai thầy trò ngồi cạnh nhau". Công đoạn 1: Xếp hai thầy trò ngồi cạnh nhau: (1, 2); (2, 1); (2, 3); (3, 2); (3, 4); (4, 3); (4, 5); (5, 4), (5, 6) (6, 5). Có 10 cách xếp. Công đoạn 2: Xếp 4 đại biểu vào 4 vị trí còn lại. Có 4! = 24 cách xếp. Theo quy tắc nhân, ta có 10.24 = 240 cách xếp hai thầy trò ngồi cạnh nhau. Vậy n(E) = 240. Từ đó \(P\left( E \right) = \frac{{240}}{{720}} = \frac{1}{3}\) Bài 9.27 trang 69 SBT Toán 10 tập 2 Kết nối tri thức Có ba cặp vợ chồng, trong đó có hai vợ chồng ông bà An đến dự một bữa tiệc. Họ được xếp ngẫu nhiên ngồi xung quanh một chiếc bàn tròn. a) Không gian mẫu có bao nhiêu phần tử. Hai cách xếp chỗ ngồi quanh bàn tròn được coi là như nhau nếu đối với mỗi người A trong nhóm, trong hai cách xếp đó, người ngồi bên trái A và bên phải A không thay đồi. b) Tính xác suất để hai vợ chồng ông bà An ngồi cạnh nhau Lời giải: a) Mỗi cách xếp chỗ ngồi quanh bàn tròn là một phần tử của không gian mẫu. Giả sử 6 chiếc ghế quanh bàn tròn được đánh số là 1, 2, ..., 6 và \({x_i}\) kí hiệu là người ngồi ở ghế mang số \(i\). Khi đó mỗi cách xếp 6 người này \(\left( {{x_1},{x_2},{x_3},{x_4},{x_5},{x_6}} \right)\) cho ta một hoán vị của tập hợp 6 người. Có tất cả 6! cách xếp chỗ ngồi cho họ. Vì ngồi xung quanh một chiếc bàn tròn nên 6 cách xếp sau đây được xem là giống nhau. Mặc dù số ghế họ ngôi có thay đổi những vị trí tương đối giữa 6 người đó là không thay đồi. \(\begin{array}{l}\left( {{x_1},{x_2},{x_3},{x_4},{x_5},{x_6}} \right){\rm{ }}\left( {{x_2},{x_3},{x_4},{x_5},{x_6},{x_1}} \right){\rm{ }}\left( {{x_3},{x_4},{x_5},{x_6},{x_1},{x_2}} \right)\\\left( {{x_4},{x_5},{x_6},{x_1},{x_2},{x_3}} \right){\rm{ }}\left( {{x_5},{x_6},{x_1},{x_2},{x_3},{x_4}} \right){\rm{ }}\left( {{x_6},{x_1},{x_2},{x_3},{x_4},{x_5}} \right)\end{array}\) Vậy có \(\frac{{6!}}{6} = 5!\)= 120 cách xếp. Do đó \(n\left( \Omega \right) = 120\). b) Gọi E là biến Cố: “Hai ông bà An ngồi cạnh nhau". Ta hãy tính xem có bao nhiều cách xếp trong đó hai ông bà An ngồi cạnh nhau. Ta coi hai ông bà An ngồi chung một ghề. Như vậy có (5 – 1)! = 4! = 24 cách xếp. Vì hai ông bà An có thề đồi chỗ cho nhau nên có 24.2= 48 cách xếp đề hai ông bà An ngồi cạnh nhau. Vậy n(E) = 48. Từ đó P(E) = \(\frac{{48}}{{120}} = \frac{2}{5}\). Bài 9.28 trang 69 SBT Toán 10 tập 2 Kết nối tri thức Một chiếc hộp đựng 6 quả cầu trắng, 4 quả cầu đỏ và 2 quả cầu đen. Chọn ngẫu nhiên 6 quả cầu. Tính xác suất để chọn được 3 quả trắng, 2 quả đỏ và 1 quả đen. Phương pháp: Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\). Lời giải: Có tất cả 6+4+2=12 quả cầu Lấy ngẫu nhiên 6 trong 12 quả có \(n\left( \Omega \right) = C_{12}^6 = 924\) cách. Gọi E là biến cố: "Chọn được 3 quả trắng, 2 quả đỏ và 1 quả đen. Chọn 3 quả cầu trắng từ 6 quả cầu trắng, có \(C_6^3 = 20\) cách chọn. Chọn 2 quả cầu đỏ từ 4 quả cầu đỏ, có \(C_4^2 = 6\)cách chọn. Chọn 1 quả cầu đen từ 2 quả cầu đen, có 2 cách chọn. Theo quy tắc nhân ta có: n(E) = 20.6.2 = 240. Do đó \(P\left( E \right) = \frac{{240}}{{924}} = \frac{{20}}{{77}}\) Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 9
|
-

Giải SBT Toán 10 trang 70, 71, 72, 73 Kết nối tri thức tập 2
Bài 1, 2, 3 trang 70, bài 4, 5, 6 trang 71 bài 7, 8, 9, 10, 11, 12, 13, 14 trang 72, bài 15, 16, 17, 18 trang 73 SBT Toán 10 KNTT tập 2. Cho tam giác ABC có AB =2, AC = 3, BC = 4. a) Tính diện tích S của tam giác. b) Tính bán kính đường tròn ngoại tiếp của tam giác.

 Tải ngay
Tải ngay