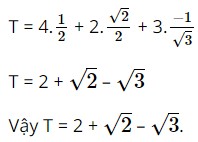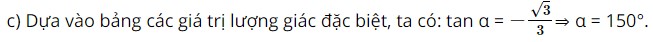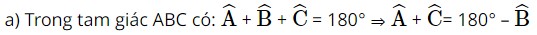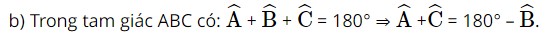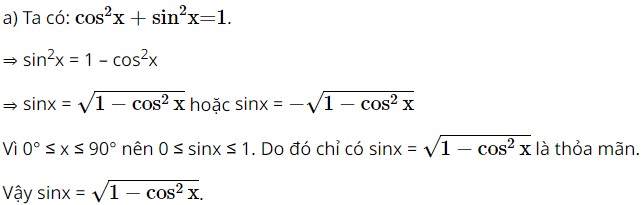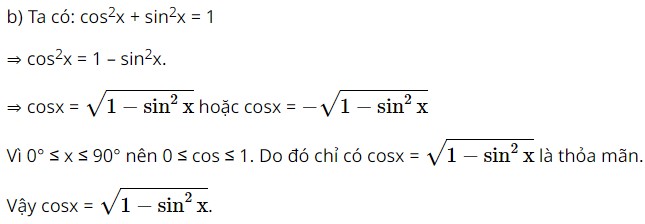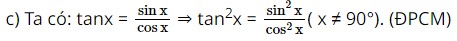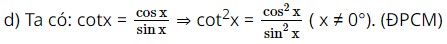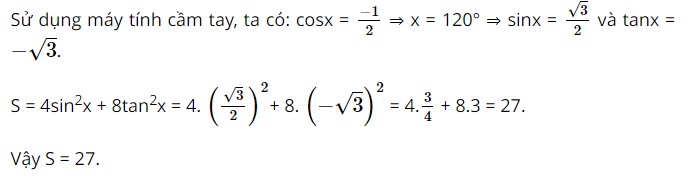Giải SBT Toán 10 trang 69 Chân trời sáng tạo tập 1Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 69, SBT Toán 10 Chân trời sáng tạo tập 1. Bài 4. Chứng minh rằng trong tam giác ABC ta có: Bài 1 trang 69 SBT Toán 10 - Chân trời sáng tạo Tính giá trị của \(T = 4\cos 60^\circ + 2\sin 135^\circ + 3\cot 120^\circ \) Lời giải: Sử dụng máy tính cầm tay ta có: T = 4cos60° + 2sin135° + 3cot120°
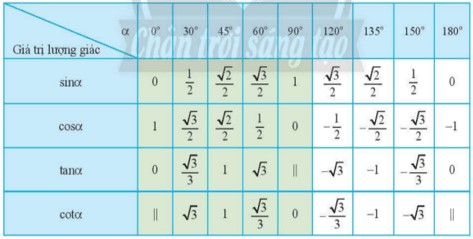
Bài 2 trang 69 SBT Toán 10 - Chân trời sáng tạo Chứng minh rằng a) \(\sin 138^\circ = \sin 42^\circ \) b) \(\tan 125^\circ = - \cot 35^\circ \) Phương pháp: a) \(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\) b) \(\tan \alpha = - \tan \left( {180^\circ - \alpha } \right)\left( {a \ne 90^\circ } \right)\) Lời giải: a) Ta có sinx = sin(180° – x ) nên: sin138° = sin (180° – 138°) = sin42°. Vậy sin138° = sin42°. b) Ta có tanx = –tan(180° – x) và tanx = cot( 90° – x ) tan125 = –tan(180° – 125°) = –tan55° = –cot( 90° – 55° ) = –cot35°. Vậy tan125° = – cot35°. Bài 3 trang 69 SBT Toán 10 - Chân trời sáng tạo Tìm góc \(\alpha \left( {0^\circ \le \alpha \le 180^\circ } \right)\) trong mỗi trường hợp sau: a) \(\cos \alpha = - \frac{{\sqrt 3 }}{2}\) b) \(\sin \alpha = \frac{{\sqrt 3 }}{2}\) c) \(\tan \alpha = - \frac{{\sqrt 3 }}{3}\) d) \(\cot \alpha = - 1\) Phương pháp: Sử dụng máy tính cầm tay hoặc tra bảng giá trị lượng giác của các góc đặc biệt. Lời giải: a) Sử dụng máy tính cầm tay, ta có được: α = 150°. b) Sử dụng máy tính cầm tay, ta có được: α = 60°. Lại có sinα = sin(180° – α ) nên α = 120°. Vậy α = 60° hoặc α = 120°.
d) Dựa vào bảng các giá trị lượng giác đặc biệt, ta có: cot α = –1 ⇒ α = 135°. Vậy α = 135°. Bài 4 trang 69 SBT Toán 10 - Chân trời sáng tạo Chứng minh rằng trong tam giác ABC ta có: a) \(\tan B = - \tan \left( {A + C} \right)\) b) \(\sin C = \sin \left( {A + B} \right)\) Phương pháp: Dựa vào mối liên hệ giữa các giá trị lượng giác giữa hai góc phụ nhau, bù nhau Lời giải:
Ta có: tanα = –tan(180° – α ) nên tanB = –tan( 180° – B ) = –tan( A+C) Vậy tanB = –tan( A+C).
Ta có: sinα = sin(180° – α ) nên sinC = sin(180° – C ) = sin ( A+B ). Vậy sinC = sin ( A+B ). Bài 5 trang 69 SBT Toán 10 - Chân trời sáng tạo Chứng minh rằng với mọi góc \(x\left( {0^\circ \le x \le 90^\circ } \right)\), ta đều có: a) \(\sin x = \sqrt {1 - {{\cos }^2}x} \) b) \(\cos x = \sqrt {1 - {{\sin }^2}x} \) c) \({\tan ^2}x = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\left( {x \ne 90^\circ } \right)\) d) \({\cot ^2}x = \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}}\left( {x \ne 0^\circ } \right)\) Lời giải:
Bài 6 trang 69 SBT Toán 10 - Chân trời sáng tạo Cho góc x với \(\cos x = - \frac{1}{2}\). Tính giá trị của biểu thức \(S = 4{\sin ^2}x + 8{\tan ^2}x\) Lời giải:
Bài 7 trang 69 SBT Toán 10 - Chân trời sáng tạo Dùng máy tính cầm tay, tính: a) \(\sin 130^\circ 12'24''\) b) \(\cos 144^\circ 35'12''\) c) \(\tan 152^\circ 35'44''\) Lời giải: Sử dụng máy tính cầm tay, ta tính được: a) sin138°12’24’’ ≈ 0,666. b) cos144°35’12’’≈ –0,815. c) tan152°35’44’’ ≈ –0,518. Bài 8 trang 69 SBT Toán 10 - Chân trời sáng tạo Dùng máy tính cầm tay, tìm x biết: a) \(\cos x = - 0,234\) b) \(\sin x = 0,812\) c) \(\cot x = - 0,333\) Lời giải: Sử dụng máy tính cầm tay, ta tính được: a) cosx = –0,234 ⇒ x ≈ 103°31’58’’. b) sinx = 0,812 ⇒ x ≈ 54°17’30’’ hay x ≈ 125°42’30’’. c) cotx = –0,333 ⇒ x ≈ 108°25’4’’. Sachbaitap.com
Xem thêm tại đây:
Bài 1. Giá trị lượng giác của một góc từ 0 đến 180 - SBT Toán 10 CTST
|
-

Giải SBT Toán 10 trang 74, 75 Chân trời sáng tạo tập 1
Giải bài 1, 2, trang 74, bài 3, 4, 5, 6, 7, 8, 9, 10 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 1. Tính độ dài các cạnh chưa biết trong các tam giác sau:

 Tải ngay
Tải ngay