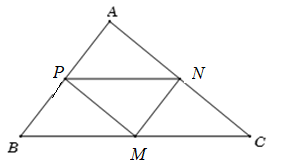
Giải SBT Toán 10 trang 73, 74 Cánh Diều tập 2Giải bài 24, 25, 26, 27, 28, 29, 30 trang 73, bài 31, 32 trang 74 SBT Toán 10 Cánh Diều tập 2. Cho đường thẳng ∆: x − 3y + 4 = 0. Phương trình nào dưới đây là phương trình tham số của ∆? Bài 24 trang 73 SBT Toán 10 - Cánh Diều Cho đường thẳng ∆: 2x − 3y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của ∆? A. \(\overrightarrow {{n_1}} = (2; - 3)\) B. \(\overrightarrow {{n_2}} = ( - 3;2)\) C. \(\overrightarrow {{n_3}} = (2;3)\) D. \(\overrightarrow {{n_4}} = (3;2)\) Lời giải: ∆: 2x − 3y + 5 = 0 có vectơ pháp tuyến là \(\overrightarrow n = (2; - 3)\) Chọn A Bài 25 trang 73 SBT Toán 10 - Cánh Diều Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 - t\\y = 4 + 2t\end{array} \right.\). Vectơ nào dưới đây là một vectơ chỉ phương của ∆? Lời giải: \(\Delta :\left\{ \begin{array}{l}x = 3 - t\\y = 4 + 2t\end{array} \right.\) có một vectơ chỉ phương là \(\overrightarrow u = ( - 1;2)\) Chọn C Bài 26 trang 73 SBT Toán 10 - Cánh Diều Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 - 5t\\y = - 1 + 3t\end{array} \right.\). Trong các điểm có tọa độ dưới đây điểm nào nằm trên đường thẳng ∆? A. (-3; -2) B. (2; -1) C. (-2; 1) D. (-5; 3) Phương pháp: Bước 1: Tìm điểm đi qua trên phương trình đường thẳng Bước 2: Nếu không có điểm trên PT, thay tọa độ các điểm và giải tìm t, nếu 2 giá trị t trong hệ giống nhau thì điểm đó thuộc ∆ Lời giải: Ta thấy điểm (2; -1) thuộc đường thẳng ∆ Chọn B Bài 27 trang 73 SBT Toán 10 - Cánh Diều Cho đường thẳng ∆: x − 3y + 4 = 0. Phương trình nào dưới đây là phương trình tham số của ∆? A. \(\left\{ \begin{array}{l}x = - 1 + 3t\\y = - 1 + t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = - 1 + 3t\\y = 1 + t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = - 1 - 3t\\y = 1 + t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 1 - t\end{array} \right.\) Lời giải: ∆ có VTPT là \(\overrightarrow n = (1; - 3) \Rightarrow \)VTCP của ∆ là \(\overrightarrow {{u_1}} = (3;1)\)hoặc \(\overrightarrow {{u_2}} = ( - 3; - 1)\) Loại C Xét điểm (-1; 1) ta có -1 – 3.1 + 4 = 0 \( \Rightarrow ( - 1;1) \in \Delta \) ∆ có VTPT là \(\overrightarrow n = (1; - 3) \Rightarrow \)VTCP của ∆ là \(\overrightarrow {{u_1}} = (3;1)\)hoặc \(\overrightarrow {{u_2}} = ( - 3; - 1)\) Loại C Xét điểm (-1; 1) ta có -1 – 3.1 + 4 = 0 \( \Rightarrow ( - 1;1) \in \Delta \) Chọn B Bài 28 trang 73 SBT Toán 10 - Cánh Diều Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = - 2 + 2t\\y = 3 - 5t\end{array} \right.\). Phương trình nào dưới đây là phương trình tổng quát của ∆? A. 5x + 2y – 4 = 0 B. 2x - 5y + 19 = 0 C. -5x + 2y – 16 = 0 D. 5x + 2y + 4 = 0 Lời giải: ∆ có VTCP là \(\overrightarrow u = (2; - 5) \Rightarrow \)VTPT của ∆ là \(\overrightarrow {{u_1}} = (5;2)\)hoặc \(\overrightarrow {{u_2}} = ( - 5; - 2)\) Loại B, C ∆ có điểm đi qua là (-2; 3) PTTQ của ∆ là: 5x + 2y + 4 = 0 Chọn D Bài 29 trang 73 SBT Toán 10 - Cánh Diều Cho tam giác ABC, biết toạ độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1 ; 1), N(3 ; 4), P(5 ; 6). a) Viết phương trình tham số của các đường thẳng AB, BC, CA b) Viết phương trình tổng quát của các đường trung trực của tam giác ABC Lời giải: a) Theo giả thiết, MN, MP, NP là các đường trung bình của ∆ABC \( \Rightarrow MN//AB,MP//AC,NP//BC\) Khi đó, AB, AC, BC lần lượt nhận các vectơ \(\overrightarrow {MN} = (4;3),\overrightarrow {MP} = (6;5),\overrightarrow {NP} = (2;2)\) làm VTCP + AB đi qua P, nhận \(\overrightarrow {MN} = (4;3)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 5 + 4t\\y = 6 + 3t\end{array} \right.\) + AC đi qua N, nhận \(\overrightarrow {MP} = (6;5)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 3 + 6k\\y = 4 + 5k\end{array} \right.\) + BC đi qua M, nhận \(\overrightarrow u = (1;1)\)cùng phương với \(\overrightarrow {NP} = (2;2)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = - 1 + p\\y = 1 + p\end{array} \right.\) b) Ta có: + Đường trung trực của cạnh AB đi qua P và nhận \(\overrightarrow {MN} = (4;3)\) làm VTPT nên có PTTQ: 4x + 3y – 38 = 0 + Đường trung trực của cạnh AC đi qua N và nhận \(\overrightarrow {MP} = (6;5)\) làm VTPT nên có PTTQ: 6x + 5y – 38 = 0 + Đường trung trực của cạnh BC đi qua M và nhận \(\overrightarrow {NP} = (2;2)\) làm VTPT nên có PTTQ: 2x + 2y = 0 \( \Leftrightarrow x + y = 0\) Bài 30 trang 73 SBT Toán 10 - Cánh Diều Cho tam giác ABC có A(3 ; 7), B(–2 ; 2), C(6 ; 1). Viết phương trình tổng quát của các đường cao của tam giác ABC. Lời giải: Ta có: \(\overrightarrow {AB} = ( - 5; - 5),\overrightarroaw {AC} = (3; - 6),\overrightarrow {BC} = (8; - 1)\) Gọi AH, BM, CN là các đường cao của ∆ABC. Khi đó: + \(AH \bot BC \Rightarrow \) AH đi qua A và nhận \(\overrightarrow {BC} = (8; - 1)\) làm VTPT nên có PT: 8x – y – 17 = 0 + \(BM \bot AC \Rightarrow \) BM đi qua B và nhận \(\overrightarrow {{n_1}} = (1; - 2)\) cùng phương với \(\overrightarrow {AC} = (3; - 6)\) làm VTPT nên có PT: x – 2y + 6 = 0 + \(CN \bot AB \Rightarrow \) CN đi qua C và nhận \(\overrightarrow {{n_2}} = (1;1)\) cùng phương với \(\overrightarrow {AB} = ( - 5; - 5)\) làm VTPT nên có PT: x + y – 7 = 0 Bài 31 trang 74 SBT Toán 10 - Cánh Diều Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 4 + t\\y = - 1 + 2t\end{array} \right.\) và điểm A(2 ; 1). Hai điểm M, N nằm trên ∆. a) Tìm toạ độ điểm M sao cho AM = \(\sqrt {17} \) b) Tìm toạ độ điểm N sao cho đoạn thẳng AN ngắn nhất Lời giải: Do \(M,N \in \Delta \) nên \(M(4 + t; - 1 + 2t)\) và \(N(4 + k; - 1 + 2k)\) a) Ta có: \(\overrightarrow {AM} = (t + 2;2t - 2)\) Theo giả thiết, AM = \(\sqrt {17} \) \( \Rightarrow A{M^2} = 17 \Leftrightarrow {(t + 2)^2} + {(2t - 2)^2} = 17\)\( \Leftrightarrow 5{t^2} - 4t - 9 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = \frac{9}{5}\end{array} \right.\) Với t = -1 thì \(M(3; - 3)\) Với \(t = \frac{9}{5}\) thì \(M\left( {\frac{{29}}{5};\frac{{13}}{5}} \right)\) Vậy có 2 điểm M thỏa mãn là \(M(3; - 3)\) và \(M\left( {\frac{{29}}{5};\frac{{13}}{5}} \right)\) b) Ta có: \(\overrightarrow {AN} = (k + 2;2k - 2)\) \(AN = \sqrt {{{\left( {k + 2} \right)}^2} + {{(2k - 2)}^2}} \)\( \Leftrightarrow A{N^2} = {\left( {k + 2} \right)^2} + {(2k - 2)^2} \Leftrightarrow A{N^2} = 5{k^2} - 4k + 8\) AN nhỏ nhất \( \Leftrightarrow A{N^2} = 5{k^2} - 4k + 8\) nhỏ nhất Ta có: \(5{k^2} - 4k + 8 = 5{\left( {k - \frac{2}{5}} \right)^2} + \frac{{44}}{5}\)\( \Rightarrow A{N^2} \ge \frac{{44}}{5} \Rightarrow AN \ge \frac{{2\sqrt {55} }}{5}\) Dấu “=” xảy ra khi và chỉ khi \(k = \frac{2}{5}\) \( \Rightarrow N\left( {\frac{{22}}{5}; - \frac{1}{5}} \right)\) Bài 32 trang 74 SBT Toán 10 - Cánh Diều Cho ba điểm A(-2 ; 2), B(7 ; 5), C(4 ; – 5) và đường thẳng ∆: 2x + y – 4 = 0 a) Tìm toạ độ điểm M thuộc ∆ và cách đều hai điểm A và B b*) Tìm toạ độ điểm N thuộc ∆ sao cho |\(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} \)| có giá trị nhỏ nhất. Lời giải: a) Gọi \(M(t;4 - 2t) \in \Delta \) Ta có: \(\overrightarrow {AM} = (t + 2; - 2t + 2)\), \(\overrightarrow {BM} = (t - 7; - 2t - 1)\) Theo giả thiết, M cách đều hai điểm A và B \( \Rightarrow AM = BM \Leftrightarrow A{M^2} = B{M^2}\) \( \Leftrightarrow {(t + 2)^2} + {( - 2t + 2)^2} = {(t - 7)^2} + {( - 2t - 1)^2}\) \( \Leftrightarrow - 4t + 8 = - 10t + 50 \Leftrightarrow 6t = 42 \Leftrightarrow t = 7\) Vậy M(7 ; -10) b*) Ta có: \(\overrightarrow {AB} = (9;3),\overrightarrow {AC} = (6; - 7)\) Vì \(\frac{9}{6} \ne \frac{3}{{ - 7}}\) nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương \( \Rightarrow A,B,C\) không thẳng hàng Gọi G là trọng tâm ∆ABC \( \Rightarrow G\left( {3;\frac{2}{3}} \right)\) và \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) Xét \(\left| {\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} } \right| = \left| {\overrightarrow {NG} + \overrightarrow {GA} + \overrightarrow {NG} + \overrightarrow {GB} + \overrightarrow {NG} + \overrightarrow {GC} } \right|\)\( = \left| {3\overrightarrow {NG} } \right| = 3NG\) \(\left| {\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} } \right|\) nhỏ nhất khi và chỉ khi NG nhỏ nhất \( \Leftrightarrow \) N là hình chiếu của G trên ∆ Gọi d là đường thẳng đi qua G, vuông góc với ∆ ∆ có VTPT \(\overrightarrow n = (2;1)\) \( \Rightarrow \) ∆ có một VTCP là \(\overrightarrow u = (1; - 2)\) Do \(d \bot \Delta \) nên d nhận \(\overrightarrow u = (1; - 2)\)làm VTPT \( \Rightarrow \) d có PT: 3x – 6y – 5 = 0 N là giao điểm của d và ∆ \( \Rightarrow \) tọa độ điểm N là nghiệm của hệ PT: \(\left\{ \begin{array}{l}2x + y - 4 = 0\\3x - 6y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{29}}{{15}}\\y = \frac{2}{{15}}\end{array} \right.\) Vậy \(N\left( {\frac{{29}}{{15}};\frac{2}{{15}}} \right)\) Sachbaitap.com
Xem thêm tại đây:
Bài 3. Phương trình đường thẳng
|
-

Giải SBT Toán 10 trang 81, 82, 83 Cánh Diều tập 2
Giải bài 33, 34, 35, 36, 37 trang ,81 bài 38, 39, 40, 4, 42, 43, 44, 45 trang 82, bài 46 trang 83, bài 17 trang 10 SBT Toán 10 Cánh Diều tập 2. Phương trình nào dưới đây là phương trình tham số của một đường thẳng song song với đường thẳng. Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau:

 Tải ngay
Tải ngay