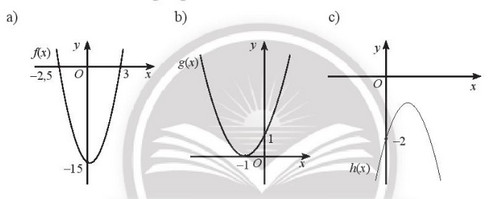
Giải SBT Toán 10 trang 8, 9, 10 Chân trời sáng tạo tập 2

Bài 1 trang 8 SBT Toán 10 - Chân trời sáng tạo

Tính biệt thức và nghiệm (nếu có) của tam thức bậc hai sau. Xác định dấu của chúng tại \(x =  - 2\)

a) \(f\left( x \right) =  - 2{x^2} + 3x - 4\)

b) \(g\left( x \right) = 2{x^2} + 8x + 8\)

c) \(h\left( x \right) = 3{x^2} + 7x - 10\)

Lời giải:

a) Biệt thức của f(x) là \(\Delta  = {3^2} - 4.\left( { - 2} \right).\left( { - 4} \right) =  - 23\)

Ta có \(\Delta  < 0\) nên tam thức bậc hai đã cho vô nghiệm

\(f( - 2) =  - 2.{( - 2)^2} + 3.( - 2) - 4 =  - 18 < 0\) nên \(f(x)\) âm tại \(x =  - 2\)

b) Biệt thức của g(x) là \(\Delta  = {8^2} - 4.2.8 = 0\)

Ta có \(\Delta  = 0\) nên tam thức bậc hai đã cho có nghiệm kép \({x_1} = {x_2} =  - 2\)

Vậy nghiệm của g(x) là \( - 2\)

Do đó \(g( - 2) = 0\) nên \(g(x)\) không âm, không dương tại \(x =  - 2\)

c) Biệt thức của h(x) là \(\Delta  = {7^2} - 4.3.\left( { - 10} \right) = 169\)

Ta có \(\Delta  > 0\) nên tam thức bậc hai đã cho có hai nghiệm là  \(x =  - \frac{{10}}{3}\) hoặc \(x = 1\)

Vậy nghiệm của h(x) là \( - \frac{{10}}{3}\) và 1

\(h( - 2) = 3.{( - 2)^2} + 7.( - 2) - 10 =  - 12 < 0\) nên \(h(x)\) âm tại \(x =  - 2\)

Bài 2 trang 9 SBT Toán 10 - Chân trời sáng tạo

Tìm giá trị của tham số m để:

a) \(f\left( x \right) = \left( {2m - 8} \right){x^2} + 2mx + 1\) là một tam thức bậc hai

b) \(f\left( x \right) = \left( {2m + 3} \right){x^2} + 3x - 4{m^2}\) là một tam thức bậc hai có \(x = 3\) là một nghiệm

c) \(f\left( x \right) = 2{x^2} + mx - 3\) dương tại \(x = 2\)

Lời giải:

a) f(x) là tam thức bậc hai khi và chỉ khi  \(2m - 8 \ne 0 \Leftrightarrow m \ne 4\)

Vậy để \(f\left( x \right)\) là tam thức bậc hai thì \(m \ne 4\)

b) f(x) là tam thức bậc hai khi và chỉ khi  \(2m + 3 \ne 0 \Leftrightarrow m \ne  - \frac{3}{2}\)

Mặt khác, \(x = 3\) là nghiệm của f(x) khi và chỉ khi \(f\left( 3 \right) = 0\)

hay \(f\left( 3 \right) = \left( {2m + 3} \right){.3^2} + 3.3 - 4{m^2} = 0 \Leftrightarrow  - 4{m^2} + 18m + 36 = 0\)

Suy ra \(m =  - \frac{3}{2}\) hoặc \(m = 6\)

Vậy để \(f\left( x \right)\) là tam thức bậc hai và có nghiệm là \(x = 3\) thì \(m = 6\)

c) Hàm số f(x) có \(a = 2 \ne 0\) nên là tam thức bậc hai

\(f\left( x \right) = 2{x^2} + mx - 3\) dương tại \(x = 2\) khi và chỉ khi \(f\left( 2 \right) > 0\)

hay \(f\left( 2 \right) = {2.2^2} + 2m - 3 > 0 \Leftrightarrow m >  - \frac{5}{2}\)

Vậy để \(f\left( x \right)\) dương tại \(x = 2\) thì \(m >  - \frac{5}{2}\)

Bài 3 trang 9 SBT Toán 10 - Chân trời sáng tạo

Tìm các giá trị của tham số m để:

a) \(f\left( x \right) = \left( {{m^2} + 9} \right){x^2} + \left( {m + 6} \right)x + 1\) là một tam thức bậc hai có một nghiệm duy nhất

b) \(f\left( x \right) = \left( {m - 1} \right){x^2} + 3x + 1\) là một tam thức bậc hai có hai nghiệm phân biệt

c) \(f\left( x \right) = m{x^2} + \left( {m + 2} \right)x + 1\) là một tam thức bậc hai vô nghiệm

Lời giải:

a) Để \(f\left( x \right)\) là tam thức bậc hai thì \({m^2} + 9 \ne 0\) đúng với mọi \(m \in \mathbb{R}\)

Mặt khác, tam thức trên có một nghiệm duy nhất khi và chỉ khi \(\Delta  = 0\)

hay \({\left( {m + 6} \right)^2} - 4.\left( {{m^2} + 9} \right) = 0 \Rightarrow  - 3{m^2} + 12m = 0\) suy ra \(m = 0\) hoặc \(m = 4\)

Vậy khi \(m = 0\) hoặc \(m = 4\) thì \(f\left( x \right) = \left( {{m^2} + 9} \right){x^2} + \left( {m + 6} \right)x + 1\) là một tam thức bậc hai có một nghiệm duy nhất

b) Để \(f\left( x \right)\) là tam thức bậc hai thì \(m - 1 \ne 0 \Leftrightarrow m \ne 1\)     (*)

Mặt khác, tam thức trên có hai nghiệm phân biệt khi và chỉ khi \(\Delta  > 0\)

hay \({3^2} - 4.\left( {m - 1} \right) > 0 \Rightarrow  - 4m + 13 > 0 \Leftrightarrow m < \frac{{13}}{4}\)        (**)

Kết hợp (*) và (**) ta được \(m \in \left( { - \infty ;\frac{{13}}{4}} \right)\backslash 1\)

Vậy khi \(m \in \left( { - \infty ;\frac{{13}}{4}} \right)\backslash 1\) thì \(f\left( x \right) = \left( {m - 1} \right){x^2} + 3x + 1\) là một tam thức bậc hai có hai nghiệm phân biệt

c) Để \(f\left( x \right)\) là tam thức bậc hai thì \(m \ne 0\)           

Mặt khác, tam thức trên vô nghiệm khi và chỉ khi \(\Delta  < 0\)

hay \({\left( {m + 2} \right)^2} - 4m < 0 \Rightarrow {m^2} + 4 < 0\)

Ta có \({m^2} \ge 0\;\forall m \in \mathbb{R} \Rightarrow {m^2} + 4 \ge 4 > 0\;\forall m \in \mathbb{R}\),

Vậy không có giá trị m thỏa mãn yêu cầu bài toán

Bài 4 trang 9 SBT Toán 10 - Chân trời sáng tạo

Dựa vào đồ thị của hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai tương ứng:

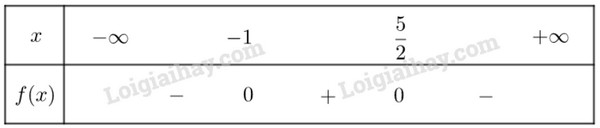
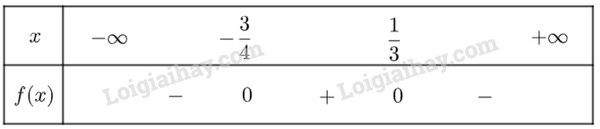
Lời giải:

a) \(f\left( x \right) > 0\) dương trên khoảng \(\left( { - \infty ; - 2,5} \right)\) và \(\left( {3; + \infty } \right)\)

   \(f\left( x \right) < 0\) âm trên khoảng \(\left( { - 2,5;3} \right)\)

b) \(g\left( x \right) > 0\) dương với mọi \(x \ne  - 1\)

c) \(h\left( x \right) < 0\) âm với mọi \(x \in \mathbb{R}\)

Bài 5 trang 9 SBT Toán 10 - Chân trời sáng tạo

Xét dấu của các tam thức bậc hai sau:

a) \(f\left( x \right) = {x^2} - 5x + 4\)   

b) \(f\left( x \right) =  - \frac{1}{3}{x^2} + 2x - 3\)

c) \(f\left( x \right) = 3{x^2} + 6x + 4\)

d) \(f\left( x \right) =  - 2{x^2} + 3x + 5\)

e) \(f\left( x \right) =  - 6{x^2} + 3x - 1\) 

g) \(f\left( x \right) = 4{x^2} + 12x + 9\)

Lời giải:

a) \(f\left( x \right) = {x^2} - 5x + 4\) có \(\Delta  = 9 > 0\) , hai nghiệm phân biết \({x_1} = 1,{x_2} = 4\) và có \(a = 1 > 0\)

Ta có bảng xét dấu \(f\left( x \right)\) như sau:

Vậy \(f\left( x \right)\) dương trong hai khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {4; + \infty } \right)\), âm trong khoảng \(\left( {1;4} \right)\)

b) \(f\left( x \right) =  - \frac{1}{3}{x^2} + 2x - 3\) có \(\Delta  = 0\) , có nghiệm kép \({x_1} = {x_2} = 3\)và có \(a =  - \frac{1}{3} < 0\)

Vậy \(f\left( x \right)\) âm với mọi \(x \ne 3\)

c) \(f\left( x \right) = 3{x^2} + 6x + 4\) có \(\Delta  =  - 12 < 0\) và có \(a = 3 > 0\)

Vậy \(f\left( x \right)\) dương với mọi \(x \in \mathbb{R}\)

d) \(f\left( x \right) =  - 2{x^2} + 3x + 5\) có \(\Delta  = 49 > 0\) , hai nghiệm phân biết \({x_1} =  - 1,{x_2} = \frac{5}{2}\) và có \(a =  - 2 < 0\)

Ta có bảng xét dấu \(f\left( x \right)\) như sau:

Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {\frac{5}{2}; + \infty } \right)\), dương trong khoảng \(\left( { - 1;\frac{5}{2}} \right)\)

e) \(f\left( x \right) =  - 6{x^2} + 3x - 1\) có \(\Delta  =  - 15 < 0\) và có \(a =  - 6 < 0\)

Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)

g) \(f\left( x \right) = 4{x^2} + 12x + 9\) có \(\Delta  = 0\) , có nghiệm kép \({x_1} = {x_2} =  - \frac{3}{2}\)và có \(a = 4 > 0\)

Vậy \(f\left( x \right)\) dương với mọi \(x \ne  - \frac{3}{2}\)

Bài 6 trang 9 SBT Toán 10 - Chân trời sáng tạo

Tìm các giá trị của tham số m để:

a) \(f\left( x \right) = \left( {m + 1} \right){x^2} + 5x + 2\) là tam thức bậc hai không đổi dấu trên \(\mathbb{R}\)

b) \(f\left( x \right) = m{x^2} - 7x + 4\) là tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)

c) \(f\left( x \right) = 3{x^2} - 4x + \left( {3m - 1} \right)\)là tam thức bậc hai dương với mọi \(x \in \mathbb{R}\)

d) \(f\left( x \right) = \left( {{m^2} + 1} \right){x^2} - 3mx + 1\) là tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)

Lời giải:

a) \(f\left( x \right)\) là tam thức bậc hai khi và khi \(m + 1 \ne 0 \Leftrightarrow m \ne  - 1\)

Mặt khác, để tam thức bậc hai không đổi dấu trên \(\mathbb{R}\) , tức là không cắt trục hoành (hay f(x)=0 vô nghiệm) khi và chỉ khi \(\Delta  < 0\)

hay \({5^2} - 4\left( {m + 1} \right).2 < 0 \Leftrightarrow  - 8m + 17 < 0 \Leftrightarrow m > \frac{{17}}{8}\)

Vậy để \(f\left( x \right) = \left( {m + 1} \right){x^2} + 5x + 2\) là tam thức bậc hai không đổi dấu trên \(\mathbb{R}\) thì \(m > \frac{{17}}{8}\)

b) \(f\left( x \right)\) là tam thức bậc hai khi và khi \(m \ne 0\)

Mặt khác, \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(a < 0\) và \(\Delta  < 0\)

hay \(\left\{ \begin{array}{l}m < 0\\{\left( { - 7} \right)^2} - 4m.4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\m > \frac{{49}}{{16}}\end{array} \right.\) (Vô lý)

Vậy không có giá trị nào của tham số m thỏa mãn yêu cầu.

c) \(f\left( x \right)\) có \(a = 3 > 0\), suy ra \(f\left( x \right)\)  dương với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(\Delta  < 0\)

hay \({\left( { - 4} \right)^2} - 4.3.\left( {3m - 1} \right) < 0 \Leftrightarrow  - 36m + 28 < 0 \Leftrightarrow m > \frac{7}{9}\)

Vậy để \(f\left( x \right) = 3{x^2} - 4x + \left( {3m - 1} \right)\)là tam thức bậc hai dương với mọi \(x \in \mathbb{R}\) thì \(m > \frac{7}{9}\)

d) \(f\left( x \right) = \left( {{m^2} + 1} \right){x^2} - 3mx + 1\) có \(a = {m^2} + 1 > 0\forall m \in \mathbb{R}\)

mà để \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\) thì \(a < 0\) và \(\Delta  < 0\)

Vậy không tồn tại giá trị m để \(f\left( x \right) = \left( {{m^2} + 1} \right){x^2} - 3mx + 1\) là tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)

Bài 7 trang 10 SBT Toán 10 - Chân trời sáng tạo

Chứng minh rằng

a) \(2{x^2} + \sqrt 3 x + 1 > 0\) với mọi \(x \in \mathbb{R}\)

b) \({x^2} + x + \frac{1}{4} \ge 0\) với mọi \(x \in \mathbb{R}\)

c) \( - {x^2} <  - 2x + 3\) với mọi \(x \in \mathbb{R}\)

Lời giải:

a) Tam thức \(2{x^2} + \sqrt 3 x + 1\) có \(\Delta  = {\left( {\sqrt 3 } \right)^2} - 4.2 =  - 5 < 0\) và \(a = 2 > 0\)

Suy ra \(2{x^2} + \sqrt 3 x + 1 > 0\forall x \in \mathbb{R}\)  (đpcm)

b) Tam thức \({x^2} + x + \frac{1}{4}\) có \(\Delta  = {1^2} - 4.\frac{1}{4} = 0\), có nghiệm kép \(x =  - \frac{1}{2}\) và \(a = 1 > 0\)

Suy ra \({x^2} + x + \frac{1}{4} \ge 0\) với mọi \(x \in \mathbb{R}\)  (đpcm)

c) \( - {x^2} <  - 2x + 3\) với mọi \(x \in \mathbb{R}\)         \( \Leftrightarrow {x^2} - 2x + 3 > 0\) với mọi \(x \in \mathbb{R}\)

Xét tam thức \({x^2} - 2x + 3\) ta có \(\Delta  = {\left( { - 2} \right)^2} - 4.3 =  - 8 < 0\) và \(a = 1 > 0\)

Suy ra \({x^2} - 2x + 3 > 0\) với mọi \(x \in \mathbb{R}\)\( \Leftrightarrow  - {x^2} <  - 2x + 3\)      (đpcm)

Bài 8 trang 10 SBT Toán 10 - Chân trời sáng tạo

Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) trong mỗi trường hợp sau:

a) Đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { - 1; - 4} \right),\left( {0;3} \right)\) và \(\left( {1; - 14} \right)\)

b) Đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; - 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\)

c) \(f\left( { - 5} \right) = 33,f\left( 0 \right) = 3\) và \(f\left( 2 \right) = 19\)

Lời giải:

a) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)

Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { - 1; - 4} \right),\left( {0;3} \right)\) và \(\left( {1; - 14} \right)\) nên thay tọa độ của ba điểm vào phương trình tổng quát ta có:

\(\left\{ \begin{array}{l} - 4 = a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + c\\3 = a{.0^2} + b.0 + c\\ - 14 = a{\left( 1 \right)^2} + b\left( 1 \right) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b + c =  - 4\\c = 3\\a + b + c =  - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 12\\b =  - 5\\c = 3\end{array} \right.\)

Từ a, b, c đã xác định được ta có \(\Delta  = 169 > 0\), tam thức có hai nghiệm phân biệt \(x =  - \frac{3}{4}\) và \(x = \frac{1}{3}\), trong đó \(a =  - 12 < 0\)

Ta có bảng biến thiên sau đây

Vậy tam thức đã cho có dạng là \(f\left( x \right) =  - 12{x^2} - 5x + 3\) dương trên khoảng \(\left( { - \frac{3}{4};\frac{1}{3}} \right)\), âm trên khoảng \(\left( { - \infty ; - \frac{3}{4}} \right)\) và \(\left( {\frac{1}{3}; + \infty } \right)\)

b) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)

Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; - 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\)

 nên thay tọa độ của ba điểm vào phương trình tổng quát ta có:

\(\left\{ \begin{array}{l} - 2 = a{.0^2} + b.0 + c\\6 = a{.2^2} + b.2 + c\\13 = a{.3^2} + b.3 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c =  - 2\\4a + 2b + c = 6\\9a + 3b + c = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c =  - 2\end{array} \right.\)

Từ a, b, c đã xác định được ta có \(\Delta  = 12 > 0\), tam thức có hai nghiệm phân biệt \(x =  - 1 - \sqrt 3 \) và \(x =  - 1 + \sqrt 3 \), trong đó \(a = 1 > 0\)

Ta có bảng biến thiên sau đây

Vậy tam thức đã cho có dạng là \(f\left( x \right) = {x^2} + 2x - 2\) âm  trên khoảng \(\left( { - 1 - \sqrt 3 ; - 1 + \sqrt 3 } \right)\), dương trên khoảng \(\left( { - \infty ; - 1 - \sqrt 3 } \right)\) và \(\left( { - 1 + \sqrt 3 ; + \infty } \right)\)

c) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)

Vì \(f\left( { - 5} \right) = 33\) nên \(a.{( - 5)^2} + b.( - 5) + c = 33\)

Vì \(f\left( 0 \right) = 3\) nên \(a{.0^2} + b.0 + c = 3\)

Vì \(f\left( 2 \right) = 19\) nên \(a{.2^2} + b.2 + c = 19\)

Từ đó ta có hệ

\(\left\{ \begin{array}{l}a.{( - 5)^2} + b.( - 5) + c = 33\\a{.0^2} + b.0 + c = 3\\a{.2^2} + b.2 + c = 19\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25a - 5b + c = 33\\c = 3\\4a + 2b + c = 19\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25a - 5b = 30\\4a + 2b = 16\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\\c = 3\end{array} \right.\)

Vậy \(f(x) = 2{x^2} + 4x + 3\), có \(\Delta ' = {2^2} - 2.3 =  - 2 < 0\) và \(a = 2 > 0\)nên \(f(x) > 0\) với mọi \(x \in \mathbb{R}\).

Sachbaitap.com