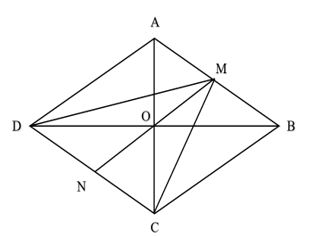
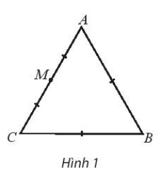
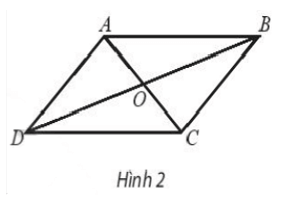
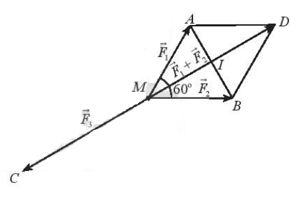
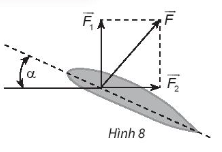
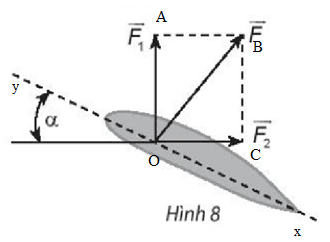
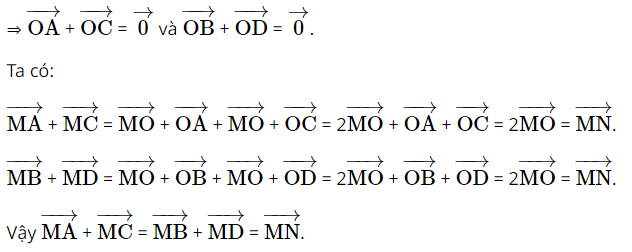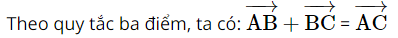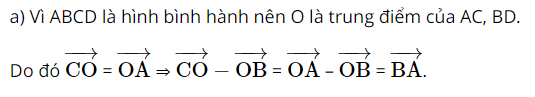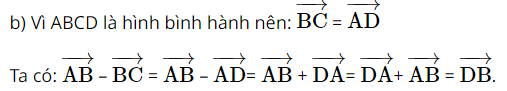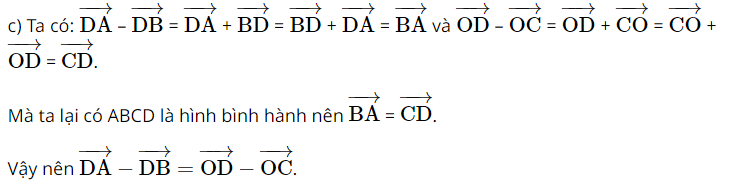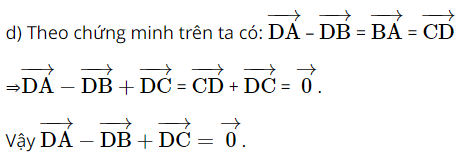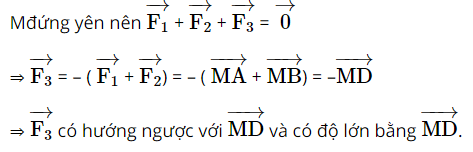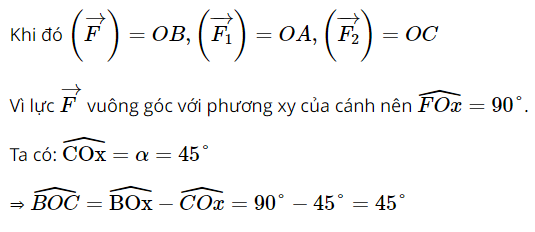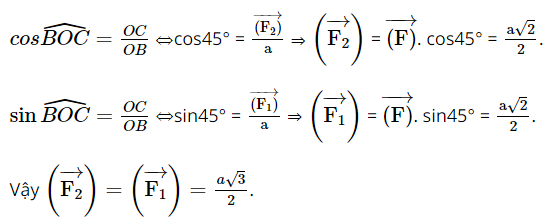Giải SBT Toán 10 trang 94 Chân trời sáng tạo tập 1Giải bài 1, 2, 3, 4, 5, 6, 7 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 2. Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có: Bài 1 trang 94 SBT Toán 10 - Chân trời sáng tạo Cho hình thoi ABCD và M là trung điểm của cạnh AB, N là trung điểm cạnh CD. Chứng minh rằng: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} = \overrightarrow {MN} \) Phương pháp: Sử dụng tính chất trung điểm \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) (với M là trung điểm của BC) Lời giải: Gọi O là tâm hình thoi. O là trung điểm của AC và BD ( tính chất hình thoi). Bài 2 trang 94 SBT Toán 10 - Chân trời sáng tạo Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có: a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) b) \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CB} - \overrightarrow {CD} \) Phương pháp: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} \) và phép trừ vectơ \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) Lời giải: a) Sử dụng quy tắc ba điểm ta có: \(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 \end{array}\) b) \(\begin{array}{l}\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} ;\overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {DB} \\ \Rightarrow \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CB} - \overrightarrow {CD} \end{array}\) Bài 3 trang 94 SBT Toán 10 - Chân trời sáng tạo Cho tam giác đều ABC cạnh a. Tính độ dài của các vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) và \(\overrightarrow {AB} - \overrightarrow {BC} \) Phương pháp: Bước 1: Xác định vectơ tổng và vectơ hiệu dựa vào các quy tắc cộng, trừ vectơ Bước 2: Xác định độ dài các cạnh dưới dấu vectơ đã tìm được ở bước 1 Lời giải: Tam giác ABC đều cạnh bằng a nên AC = a. Bài 4 trang 94 SBT Toán 10 - Chân trời sáng tạo Cho hình bình hành ABCD có tâm O. Chứng minh rằng: a) \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {BA} \) b) \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {DB} \) c) \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {OD} - \overrightarrow {OC} \) d) \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \) Phương pháp: Sử dụng tính chất của phép cộng, trừ vectơ và quy tắc ba điểm Lời giải: Bài 5 trang 94 SBT Toán 10 - Chân trời sáng tạo Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết độ lớn của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là 100N và \(\widehat {AMB} = 60^\circ \). Tìm độ lớn của lực \(\overrightarrow {{F_3}} \) Phương pháp: Điểm M dưới tác động của 3 lực nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \) Và áp dụng các tính chất của phép cộng của vectơ, quy tắc hình bình hành Lời giải: Dựng hình bình hành MADB. Gọi I là giao điểm của AB và MD. Khi đó I là trung điểm của AB và MD. Bài 6 trang 94 SBT Toán 10 - Chân trời sáng tạo Khi máy bay nghiêng cánh một góc \(\alpha \), lực \(\overrightarrow F \) của không khí tác động vuông góc với cánh và bằng tổng của lực nâng \(\overrightarrow {{F_1}} \) và lực cản \(\overrightarrow {{F_2}} \) (hình 8). Cho biết \(\alpha = 45^\circ \) và \(\left| {\overrightarrow F } \right| = a\). Tính \(\left| {\overrightarrow {{F_1}} } \right|\) và \(\left| {\overrightarrow {{F_2}} } \right|\) Lời giải: Đặt tên các điểm trong hình vẽ, ta có: Xét tam giác BOC vuông tại C, có: Bài 7 trang 94 SBT Toán 10 - Chân trời sáng tạo Cho hình vuông ABCD có tâm O và có cạnh bằng a. Cho 2 điểm M, N thỏa mãn: \(\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 ;\overrightarrow {NB} + \overrightarrow {ND} + \overrightarrow {NC} = \overrightarrow 0 \) Tìm độ dài các vectơ \(\overrightarrow {MA} ,\overrightarrow {NO} \) Lời giải: Áp dụng vào tính chất của trung điểm và trọng tâm của tam giác ta có: \(\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 \) suy ra M là trung điểm của AD Từ đó ta có: \(\overrightarrow {MA} = \frac{1}{2}\overrightarrow {DA} \Rightarrow \left| {\overrightarrow {MA} } \right| = \frac{1}{2}\left| {\overrightarrow {DA} } \right| = \frac{1}{2}DA = \frac{a}{2}\) \(\overrightarrow {NB} + \overrightarrow {ND} + \overrightarrow {NC} = \overrightarrow 0 \) suy ra N là trọng tâm của tam giác BCD Suy ra \(\overrightarrow {NO} = \frac{1}{3}\overrightarrow {CO} \Rightarrow \left| {\overrightarrow {NO} } \right| = \frac{1}{3}\left| {\overrightarrow {CO} } \right| = \frac{1}{3}CO\) Ta tính được \(AC = BD = a\sqrt 2 \Rightarrow CO = \frac{{a\sqrt 2 }}{2}\) \( \Rightarrow \left| {\overrightarrow {NO} } \right| = \frac{1}{3}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{6}\) Vậy độ dài các vectơ \(\overrightarrow {MA} ,\overrightarrow {NO} \) lần lượt là \(\frac{a}{2};\frac{{a\sqrt 2 }}{6}\) Sachbaitap.com
Xem thêm tại đây:
Bài 2. Tổng và hiệu của hai vectơ - SBT Toán 10 CTST
|
-

Giải SBT Toán 10 trang 96, 97 Chân trời sáng tạo tập 1
Giải bài 1 trang 96, bài 2, 3, 4, 5, 6 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 1. Cho hình bình hành ABCD có G là trọng tâm của tam giác ABD.

 Tải ngay
Tải ngay