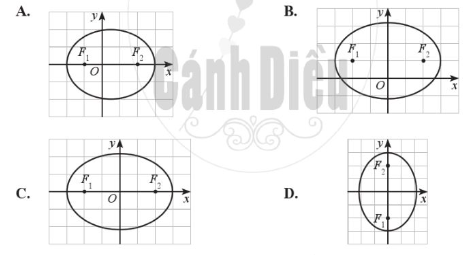
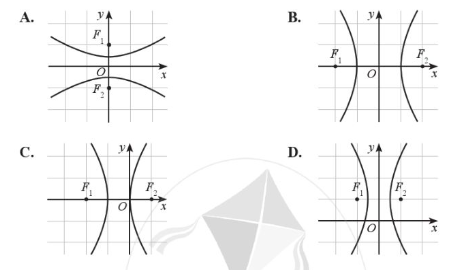
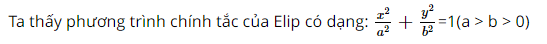Giải SBT Toán 10 trang 95, 96, 97 Cánh Diều tập 2

Bài 59 trang 95 SBT Toán 10 - Cánh Diều

Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)?

Phương pháp:

Đường elip trên hệ trục tọa độ Oxy có 2 tiêu điểm F₁, F₂ nằm trên trục Ox và đối xứng nhau qua gốc O 

Lời giải:

Khi cho x = 0 ta được y = ±b

Khi cho y = 0 ta được x = ±a

Do đó suy ra Elip đối xứng qua trục Ox và Oy và có tiêu điểm F1, F2 nằm trên trục Ox.

Vậy chọn đáp án C.

Bài 60 trang 95 SBT Toán 10 - Cánh Diều

Phương trình nào sau đây là phương trình chính tắc của elip?

A. \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)                    B. \(\frac{{{x^2}}}{{{3^2}}} - \frac{{{y^2}}}{{{3^2}}} = 1\)                        C. \(\frac{{{x^2}}}{6} + {y^2} = 1\)             D. \(\frac{{{x^2}}}{{{2^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)

Phương pháp:

Elip trong hệ trục tọa độ có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)

Lời giải:

Vậy chọn đáp án C.

Bài 61 trang 96 SBT Toán 10 - Cánh Diều

Hypebol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:

\(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)?

Phương pháp:

Đường hypebol trên hệ trục tọa độ Oxy có 2 tiêu điểm F₁, F₂ nằm trên trục Ox và đối xứng nhau qua gốc O

Lời giải:

Thì có tiêu điểm nằm trên trục Ox.

Cho y = 0 ta được x = ±a

Do đó Hypebol này đối xứng qua trục Oy.

Vậy ta chọn đáp án B.

Bài 62 trang 96 SBT Toán 10 - Cánh Diều

Phương trình nào sau đây là phương trình chính tắc của hypebol?

A. \({x^2} + \frac{{{y^2}}}{{{3^2}}} = 1\)               B. \(\frac{{{x^2}}}{{16}} - {y^2} =  - 1\)           C. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{9} =  - 1\)   D. \({x^2} - \frac{{{y^2}}}{2} = 1\)

Phương pháp:

Hypebol trong hệ trục tọa độ Oxy có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)

Lời giải:

Do đó chỉ có phương trình ở ý D là thỏa mãn.

Vậy ta chọn đáp án D.

Bài 63 trang 96 SBT Toán 10 - Cánh Diều

Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:

\({y^2} = 2px\) (p > 0)?

Phương pháp:

Đường parabol \({y^2} = 2px\) (p > 0) trong hệ trục tọa độ Oxy có bề lõm quay sang bên phải, đỉnh parabol là gốc O

Lời giải:

Parabol có dạng y² = 2px (p > 0).

Ta thấy Parabol đối xứng qua trục Ox.

Do p > 0 nên x ≥ 0 thì hàm số có nghĩa, do đó đồ thị nằm bên phải trục Oy.

Vậy chọn đáp án A.

Bài 64 trang 97 SBT Toán 10 - Cánh Diều

Phương trình nào sau đây là phương trình chính tắc của hypebol?

A. \({y^2} =  - 0,3x\)              B. \({x^2} = 0,3y\)                 

C. \({y^2} = 0,3x\)                       D. \({x^2} =  - 0,3y\)

Lời giải:

Xét đáp án C ta có: PT \({y^2} = 0,3x\) có dạng \({y^2} = 2px\) với \(p = 0,15 > 0\) nên là PT hypebol

Chọn C

Bài 65 trang 97 SBT Toán 10 - Cánh Diều

Lập phương trình chính tắc của elip (E) biết (E) đi qua hai điểm:

\(P\left( {2;\frac{{3\sqrt 3 }}{2}} \right)\) và \(Q\left( {2\sqrt 2 ;\frac{{3\sqrt 2 }}{2}} \right)\)

Phương pháp:

Bước 1: Thay tọa độ P và Q vào PT chính tắc của Elip để tìm giá trị a và b

Bước 2: Viết PT chính tắc của elip với a và b tìm được ở bước 

Lời giải:

Gọi elip cần lập PT chính tắc là (E). Khi đó (E) có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)

Do \(P\left( {2;\frac{{3\sqrt 3 }}{2}} \right) \in (E)\) nên \(\frac{{{2^2}}}{{{a^2}}} + \frac{{{{\left( {\frac{{3\sqrt 3 }}{2}} \right)}^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{4}{{{a^2}}} + \frac{{27}}{{4{b^2}}} = 1\)

Do \(Q\left( {2\sqrt 2 ;\frac{{3\sqrt 2 }}{2}} \right) \in (H)\) nên \(\frac{{{{\left( {2\sqrt 2 } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {\frac{{3\sqrt 2 }}{2}} \right)}^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{8}{{{a^2}}} + \frac{9}{{2{b^2}}} = 1\)

Ta có hệ PT: \(\left\{ \begin{array}{l}\frac{4}{{{a^2}}} + \frac{{27}}{{4{b^2}}} = 1\\\frac{8}{{{a^2}}} + \frac{9}{{2{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{{{a^2}}} = \frac{1}{{16}}\\\frac{1}{{{b^2}}} = \frac{1}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 9\end{array} \right.\)

Vậy elip (E) có PT: \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)

Bài 66 trang 97 SBT Toán 10 - Cánh Diều

Cho elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\). Tìm điểm P thuộc (E) thoả mãn OP = 2,5.

Phương pháp:

Bước 1: Tham số hóa tọa độ điểm P và thay tọa độ P vào PT (E)

Bước 2: Lập hệ PT 2 ẩn m², n² theo giả thiết

Bước 3: Giải hệ PT tìm tọa độ điểm P

Lời giải:

Giả sử điểm P có tọa độ P(m ; n)

Do \(P \in (E)\) nên \(\frac{{{m^2}}}{9} + \frac{{{n^2}}}{4} = 1\)

Theo giả thiết, \(OP = 2,5 \Rightarrow O{P^2} = 6,25 \Leftrightarrow {m^2} + {n^2} = 6,25\)

Ta có hệ PT: \(\left\{ \begin{array}{l}{m^2} + {n^2} = 6,25\\\frac{{{m^2}}}{9} + \frac{{{n^2}}}{4} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = \frac{{81}}{{20}}\\{n^2} = \frac{{11}}{5}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m =  \pm \frac{{9\sqrt 5 }}{{10}}\\n =  \pm \frac{{\sqrt {55} }}{5}\end{array} \right.\)

Vậy có 4 điểm P thỏa mãn là: \({P_1}\left( {\frac{{9\sqrt 5 }}{{10}};\frac{{\sqrt {55} }}{5}} \right),{P_2}\left( { - \frac{{9\sqrt 5 }}{{10}};\frac{{\sqrt {55} }}{5}} \right),{P_3}\left( {\frac{{9\sqrt 5 }}{{10}}; - \frac{{\sqrt {55} }}{5}} \right),{P_4}\left( { - \frac{{9\sqrt 5 }}{{10}}; - \frac{{\sqrt {55} }}{5}} \right)\)

Bài 67 trang 97 SBT Toán 10 - Cánh Diều

Lập phương trình chính tắc của hypebol (H), biết (H) đi qua hai điểm M(-1 ; 0) và \(N(2;2\sqrt 3 )\)

Lời giải:

Gọi hypebol cần lập PT chính tắc là (H). Khi đó (H) có dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)

Do \(M\left( { - 1;0} \right) \in (H)\) nên \(\frac{{{{( - 1)}^2}}}{{{a^2}}} = 1 \Leftrightarrow \frac{1}{{{a^2}}} = 1 \Leftrightarrow {a^2} = 1\)

Do \(N\left( {2;2\sqrt 3 } \right) \in (H)\) nên \(\frac{{{2^2}}}{{{a^2}}} - \frac{{{{\left( {2\sqrt 3 } \right)}^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{4}{1} - \frac{{12}}{{{b^2}}} = 1 \Leftrightarrow {b^2} = 4\)

Vậy hypebol (H) có PT: \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{4} = 1\)

Bài 68 trang 97 SBT Toán 10 - Cánh Diều

Cho hypebol (H) có phương trình chính tắc: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với a > 0, b > 0 và  đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.

Lời giải:

Do \(P,Q \in d:y = n\) nên \(P(t;n),Q(k;n)\)

Do \(P,Q \in (H)\) nên \(\left\{ \begin{array}{l}\frac{{{t^2}}}{{{a^2}}} - \frac{{{n^2}}}{{{b^2}}} = 1\\\frac{{{k^2}}}{{{a^2}}} - \frac{{{n^2}}}{{{b^2}}} = 1\end{array} \right. \Rightarrow \frac{{{t^2}}}{{{a^2}}} = \frac{{{k^2}}}{{{a^2}}}\)\( \Leftrightarrow {t^2} = {k^2} \Leftrightarrow \left\{ \begin{array}{l}t = k\\t =  - k\end{array} \right.\)

Với t = k thì P và Q trùng nhau \( \Rightarrow \) t = k không thỏa mãn

Với t = -k thì P(t ; n) và Q(-t ; n). Khi đó P và Q đối xứng nhau qua trục Oy (ĐPCM)

Bài 69 trang 97 SBT Toán 10 - Cánh Diều

Viết phương trình chính tắc của parabol (P), biết:

a) Phương trình đường chuẩn của (P) là \(x + \frac{1}{8} = 0\)

b) (P) đi qua điểm M(1 ; -8)

Lời giải:

PT chính tắc của parabol (P) có dạng y² = 2px (p > 0)

a) Theo giả thiết, phương trình đường chuẩn của (P) là \(x + \frac{1}{8} = 0\) \( \Rightarrow p = \frac{1}{4}\)

Vậy PT chính tắc của (P) là: \({y^2} = \frac{1}{2}x\)

b) Do \(M(1; - 8) \in (P)\) nên \({( - 8)^2} = 2p.1 \Rightarrow p = 32\)

Vậy PT chính tắc của (P) là: \({y^2} = 64x\)

Bài 70 trang 97 SBT Toán 10 - Cánh Diều

Cho parabol (P) có phương trình chính tắc: y² = 2px (p > 0) và đường thẳng x = m (m > 0) cắt (P) tại hai điểm I, K phân biệt. Chứng minh hai điểm I và K đối xứng nhau qua trục Ox.

Lời giải:

Do \(I,K \in d:x = m\) nên \(I(m;t),K(m;k)\)

Do \(I,K \in (P)\) nên \(\left\{ \begin{array}{l}{t^2} = 2pm\\{k^2} = 2pm\end{array} \right.\)\( \Leftrightarrow {t^2} = {k^2} \Leftrightarrow \left\{ \begin{array}{l}t = k\\t =  - k\end{array} \right.\)

Với t = k thì I và K trùng nhau \( \Rightarrow \) t = k không thỏa mãn

Với t = -k thì I(m ; t) và K(m ; -t). Khi đó I và K đối xứng nhau qua trục Ox (ĐPCM)

Sachbaitap.com