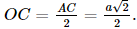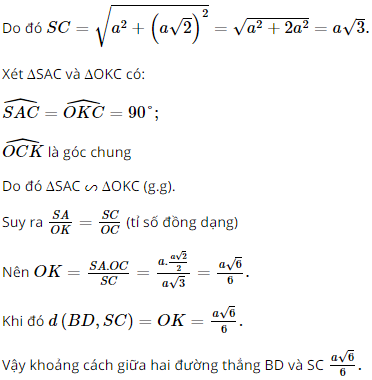Giải SGK Toán 11 Cánh Diều tập 2 trang 106Giải bài 1, 2, 3, 4, 5 trang 106 SGK Toán lớp 11 Cánh Diều tập 2. Với giả thiết ở Bài tập 2, hãy: a) Chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC. Bài 1 trang 106 SGK Toán 11 - Cánh Diều tập 2 Hình 76 gợi nên hình ảnh hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa \(\left( P \right)\) và \(\left( Q \right)\) là bao nhiêu mét?
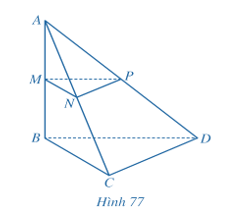
Phương pháp: Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách từ một điểm trên mặt phẳng này đến mặt phẳng còn lại. Lời giải: Do hai mặt phẳng (P) và (Q) song song với nhau nên khoảng cách giữa (P) và (Q) bằng chiều cao của cột gỗ. Vậy khoảng cách giữa (P) và (Q) bằng 4,2 m. Bài 2 trang 106 SGK Toán 11 - Cánh Diều tập 2 Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77). a) Tính khoảng cách từ điểm \(C\) đến đường thẳng \(AB\). b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\). c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(C{\rm{D}}\).
Phương pháp: ‒ Cách tính khoảng cách từ một điểm đến một đường thẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên đường thẳng. ‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng. ‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau: Cách 1: Dựng đường vuông góc chung. Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại. Lời giải:
Suy ra d(C, AB) = CB = b. Vậy khoảng cách từ điểm C đến đường thẳng AB bằng b.
Ta có: AB ⊥ CB, AB ⊥ BD và CB ∩ BD = B trong (BCD). Suy ra AB ⊥ (BCD). Mà CD ⊂ (BCD) nên AB ⊥ CD.
Ta có: CD ⊥ AB, CD ⊥ BC và AB ∩ BC = B trong (ABC). Suy ra CD ⊥ (ABC). Khi đó d(D, (ABC)) = CD. Áp dụng định lí Pythagore vào tam giác BCD vuông tại C có: BD2 = BC2 + CD2 c) Ta có: BC ⊥ AB (theo câu a) và BC ⊥ CD (theo câu b). Suy ra đoạn thẳng BC là đoạn vuông góc chung của hai đường thẳng AB và CD. Do đó d(AB, CD) = BC = b. Vậy khoảng cách giữa hai đường thẳng AB và CD bằng b. Bài 3 trang 106 SGK Toán 11 - Cánh Diều tập 2 Với giả thiết ở Bài tập 2, hãy: a) Chứng minh rằng \(MN\parallel BC\). Tính khoảng cách giữa hai đường thẳng \(MN\) và \(BC\). b) Chứng minh rằng \(MP\parallel \left( {BCD} \right)\). Tính khoảng cách từ đường thẳng \(MP\) đến mặt phẳng \(\left( {BCD} \right)\). c) Chứng minh rằng \(\left( {MNP} \right)\parallel \left( {BCD} \right)\). Tính khoảng cách giữa hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {BCD} \right)\). Phương pháp: a) ‒ Sử dụng tính chất đường trung bình của tam giác. ‒ Cách tính khoảng cách giữa hai đường thẳng song song: Tính khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia. b) ‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng. ‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng. c) ‒ Cách chứng minh hai mặt phẳng song song: Chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau song song với mặt phẳng còn lại. ‒ Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách từ một điểm trên mặt phẳng này đến mặt phẳng còn lại. Lời giải:
a) Xét ∆ABC có: M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của ∆ABC. Do đó MN // BC. Do đó d(MN, BC) = d(M, BC). Mà AB ⊥ BC (theo câu a Bài tập 2) nên MB ⊥ BC, do đó d(M, BC) = MB.
d) Xét ∆ABD có: M, P lần lượt là trung điểm của AB và AD nên MP là đường trung bình của ∆ABD. Do đó MP // BD. Mà BD ⊂ (BCD) nên MP // (BCD). Suy ra d(MP, (BCD)) = d(M, (BCD)). Ta có: AB ⊥ (BCD) (theo câu b Bài tập 2) mà M ∈ AB nên MB ⊥ (ABC).
c) Do MN // BC và BC ⊂ (BCD) nên MN // (BCD). Ta có: MN // (BCD), MP // (BCD) và MN ∩ MP = M trong (MNP). Suy ra (MNP) // (BCD).
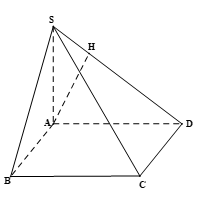
Bài 4 trang 106 SGK Toán 11 - Cánh Diều tập 2 Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\). b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\). c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\). Phương pháp: ‒ Cách tính khoảng cách từ một điểm đến một đường thẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên đường thẳng. ‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng. Lời giải:
a) Do SA ⊥ (ABCD) và CD ⊂ (ABCD) nên SA ⊥ CD. Vì ABCD là hình vuông nên CD ⊥ AD. Ta có: CD ⊥ SA, CD ⊥ AD và SA ∩ AD = A trong (SAD). Suy ra CD ⊥ (SAD). Mà SD ⊂ (SAD) nên CD ⊥ SD. Suy ra d(S, CD) = SD. Do SA ⊥ (ABCD) và AD ⊂ (ABCD) nên SA ⊥ AD. Áp dụng định lí Pythagore vào tam giác SAD vuông tại A (do SA ⊥ AD) có: SD2 = SA2 + AD2 = a2 + a2 = 2a2. b) Vì ABCD là hình vuông nên AD ⊥ AB. Ta có: AD ⊥ SA (theo câu a), AD ⊥ AB và SA ∩ AB = A trong (SAB). Suy ra AD ⊥ (SAB). Khi đó d(D, (SAB)) = AD = a. Vậy khoảng cách từ điểm D đến mặt phẳng (SAB) bằng a. c) Kẻ AH ⊥ SD (H ∈ SD). Do CD ⊥ (SAD) (theo câu a) và AH ⊂ (SAD) nên CD ⊥ AH. Ta có: AH ⊥ CD, AH ⊥ SD và CD ∩ SD = D trong (SCD). Suy ra AH ⊥ (SCD). Khi đó d(A, (SCD)) = AH. Áp dụng hệ thức lượng trong tam giác SAD vuông tại A, đường cao AH có:
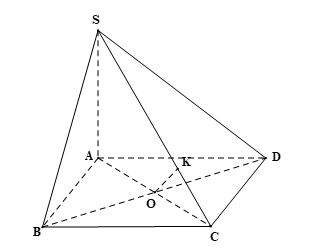
Bài 5 trang 106 SGK Toán 11 - Cánh Diều tập 2 Với giả thiết ở Bài tập 4, hãy: a) Chứng minh rằng \(BC\parallel \left( {SAD} \right)\) và tính khoảng cách giữa \(BC\) và mặt phẳng \(\left( {SAD} \right)\). b) Chứng minh rằng \(BD \bot \left( {SAC} \right)\) và tính khoảng cách giữa hai đường thẳng \(BD\) và \(SC\). Phương pháp: ‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng. ‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng. ‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trên mặt phẳng. ‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau: Cách 1: Dựng đường vuông góc chung. Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại. Lời giải:
a) Do ABCD là hình vuông nên BC // AD. Mà AD ⊂ (SAD) nên BC // (SAD). Khi đó, d(BC, (SAD)) = d(C, (SAD)) = CD = a. (vì theo câu a, CD ⊥ (SAD)) Vậy khoảng cách giữa BC và mặt phẳng (SAD) bằng a. b) Vì ABCD là hình vuông nên BD ⊥ AC. Do SA ⊥ (ABCD) và BD ⊂ (ABCD) nên SA ⊥ BD. Ta có: BD ⊥ SA, BD ⊥ AC và SA ∩ AC = A trong (SAC). Suy ra BD ⊥ (SAC). Gọi O = AC ∩ BD, kẻ OK ⊥ SC (K ∈ SC). Do BD ⊥ (SAC) và OK ⊂ (SAC) nên BD ⊥ OK. Ta có: OK ⊥ SC và OK ⊥ BD. Từ đó ta có đoạn thẳng OK là đoạn vuông góc chung của hai đường thẳng BD và SC nên d(BD, SC) = OK. Do ABCD là hình vuông nên Áp dụng định lí Pythagore trong tam giác ABC vuông tại B có: AC2 = AB2 + BC2 = a2 + a2 = 2a2. Suy ra Do O = AC ∩ BD và AC, BD là hai đường chéo của hình vuông ABCD. Suy ra O là trung điểm của AC nên Do SA ⊥ (ABCD) và AC ⊂ (ABCD) nên SA ⊥ AC. Áp dụng định lí Pythagore trong tam giác SAC vuông tại A (do SA ⊥ AC) có: SC2 = SA2 + AC2.
Sachbaitap.com
Xem thêm tại đây:
Bài 5. Khoảng cách
|
-

Giải SGK Toán 11 Cánh Diều tập 2 trang 115
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 115 SGK Toán lớp 11 Cánh Diều tập 2.Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3 g/cm.

 Tải ngay
Tải ngay

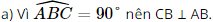

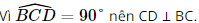
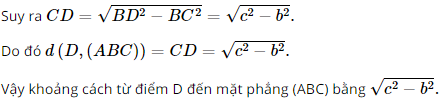
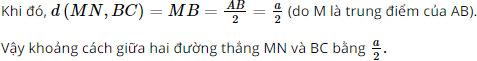
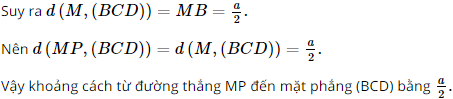


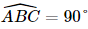 do đó tam giác ABC vuông tại B.
do đó tam giác ABC vuông tại B.