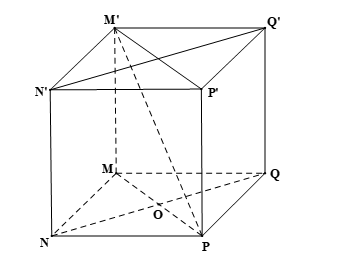
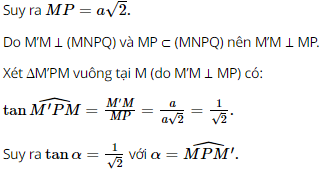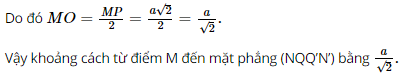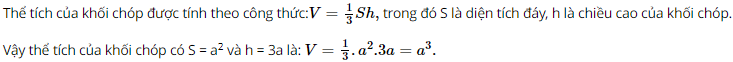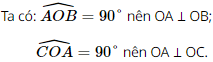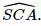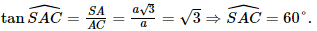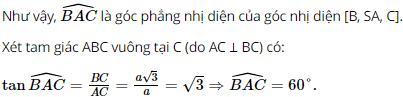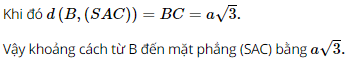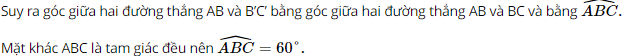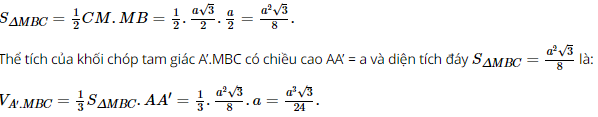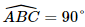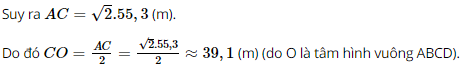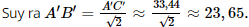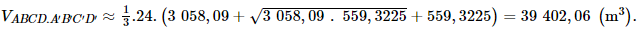Giải SGK Toán 11 Cánh Diều tập 2 trang 116, 117

Bài 1 trang 116 SGK Toán 11 - Cánh Diều tập 2

Cho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\).

a) Góc giữa hai đường thẳng \(MN\) và \(M'P\) bằng:

A. \({30^ \circ }\).                 

B. \({45^ \circ }\).                 

C. \({60^ \circ }\).                  

D. \({90^ \circ }\).

b) Gọi \(\alpha \) là số đo góc giữa đường thẳng \(M'P\) và mặt phẳng \(\left( {MNPQ} \right)\). Giá trị \(\tan \alpha \) bằng:

A. 1.                                            

B. 2.                                            

C. \(\sqrt 2 \).                         

D. \(\frac{1}{{\sqrt 2 }}\).

c) Số đo của góc nhị diện \(\left[ {N,MM',P} \right]\) bằng:

A. \({30^ \circ }\).                 

B. \({45^ \circ }\).                 

C. \({60^ \circ }\).                  

D. \({90^ \circ }\).

d) Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {NQQ'N'} \right)\) bằng:

A. \(a\).                                    

B. \(\frac{a}{{\sqrt 2 }}\).  

C. \(a\sqrt 2 \).                      

D. \(\frac{a}{2}\).

Phương pháp:

a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)

Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).

Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\).

Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).

Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.

Lời giải:

a) Đáp án đúng là: B

Vì MNPQ.M’N’P’Q’ là hình lập phương nên MM’ // PP’ và MM’ = PP’.

Suy ra M’P’PM là hình bình hành. Do đó MP // M’P’.

Vậy góc giữa hai đường thẳng MN và M’P’ bằng 45°.

b) Đáp án đúng là: D

Vì MNPQ.M’N’P’Q’ là hình lập phương nên M’M ⊥ (MNPQ).

Khi đó, MP là hình chiếu của M’P trên (MNPQ).

Áp dụng định lí Pythagore trong tam giác MNP vuông tại N có:

MP² = MN² + NP² = a² + a² = 2a²

c) Đáp án đúng là: B

Do M’M ⊥ (MNPQ) và MN ⊂ (MNPQ), MP ⊂ (MNPQ).

Suy ra M’M ⊥ MN và M’M ⊥ MP.

Mà MN ∩ MP = M ∈ M’M.

Vậy số đo của góc nhị diện [N, MM’, P] bằng 45°.

d) Đáp án đúng là: B

Gọi O là giao điểm của MP và NQ.

Vì MNPQ là hình vuông nên MO ⊥ NQ.

Do MNPQ.M’N’P’Q’ là hình lập phương nên N’N ⊥ (MNPQ).

Mà MO ⊂ (MNPQ) nên N’N ⊥ MO.

Ta có: MO ⊥ NQ, MO ⊥ N’N và NQ ∩ N’N = N trong (NQQ’N’).

Suy ra MO ⊥ (NQQ’N’).

Khi đó, d(M, (NQQ’N’)) = MO.

Vì MNPQ là hình vuông và O = MP ∩ NQ nên O là trung điểm của MP.

Vậy số đo của góc nhị diện [N, MM’, P] bằng 45°.

d) Đáp án đúng là: B

Gọi O là giao điểm của MP và NQ.

Vì MNPQ là hình vuông nên MO ⊥ NQ.

Do MNPQ.M’N’P’Q’ là hình lập phương nên N’N ⊥ (MNPQ).

Mà MO ⊂ (MNPQ) nên N’N ⊥ MO.

Ta có: MO ⊥ NQ, MO ⊥ N’N và NQ ∩ N’N = N trong (NQQ’N’).

Suy ra MO ⊥ (NQQ’N’).

Khi đó, d(M, (NQQ’N’)) = MO.

Vì MNPQ là hình vuông và O = MP ∩ NQ nên O là trung điểm của MP.

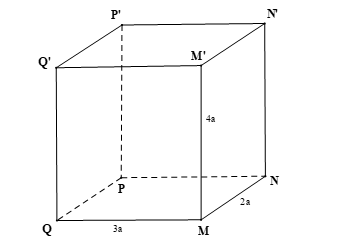
Bài 2 trang 116 SGK Toán 11 - Cánh Diều tập 2

Cho hình hộp chữ nhật \(MNPQ.M'N'P'Q'\) có \(MN = 2a,MQ = 3a,\) \(MM' = 4a\). Khoảng cách giữa hai đường thẳng \(NP\) và \(M'N'\) bằng:

A. \(2a\).                                  

B. \(3a\).                                  

C. \(4a\).                                  

D. \(5a\).

Phương pháp:

Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

Lời giải:

Đáp án đúng là: C

Vì MNPQ.M’N’P’Q’ là hình hộp chữ nhật nên ta có:

⦁ NN’ ⊥ (MNPQ) mà NP ⊂ (MNPQ) nên NN’ ⊥ NP;

⦁ NN’ ⊥ (M’N’P’Q’) mà M’N’ ⊂ (MNPQ) nên NN’ ⊥ M’N’.

Từ các kết quả trên ta có đoạn thẳng NN’ là đoạn vuông góc chung của hai đường thẳng NP và M’N’.

Suy ra d(NP, M’N’) = NN’.

Do MNPQ.M’N’P’Q’ là hình hộp chữ nhật nên NN’ = MM’ = 4a.

Vậy khoảng cách giữa hai đường thẳng NP và M’N’ bằng 4a.

Bài 3 trang 116 SGK Toán 11 - Cánh Diều tập 2

Cho khối lăng trụ có diện tích đáy bằng \({a^2}\) và chiều cao bằng \(3a\). Thể tích của khối lăng trụ đó bằng:

A. \({a^3}\).                            

B. \(3{a^3}\).                          

C. \(\frac{{{a^3}}}{3}\).      

D. \(9{a^3}\).

Phương pháp:

Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).

Lời giải:

Đáp án đúng là: B

Thể tích của khối lăng trụ được tính theo công thức: V = Sh, trong đó S là diện tích đáy, h là chiều cao của khối lăng trụ.

Vậy thể tích của khối lăng trụ có S = a² và h = 3a là:

V = a².3a = 3a³.

Bài 4 trang 116 SGK Toán 11 - Cánh Diều tập 2

Cho khối chóp có diện tích đáy là \({a^2}\) và chiều cao là \(3a\). Thể tích của khối chóp bằng:

A. \({a^3}\).                            

B. \(3{a^3}\).                          

C. \(\frac{{{a^3}}}{3}\).      

D. \(9{a^3}\).

Phương pháp:

Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải:

Đáp án đúng là: A

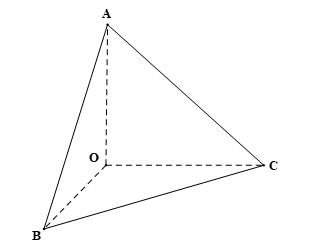
Bài 5 trang 116 SGK Toán 11 - Cánh Diều tập 2

Cho tứ diện \(OABC\) thoả mãn \(OA = a,OB = b,OC = c,\) \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {90^ \circ }\). Thể tích của khối tứ diện \(OABC\) bằng:

A. \(abc\).                                

B. \(\frac{{abc}}{2}\).          

C. \(\frac{{abc}}{3}\).           

D. \(\frac{{abc}}{6}\).

Phương pháp:

Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải:

Đáp án đúng là: D

Mà OB ∩ OC = O trong (OBC).

Suy ra OA ⊥ (OBC).

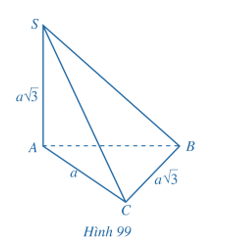
Bài 6 trang 116 SGK Toán 11 - Cánh Diều tập

Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AC \bot BC,\)\(SA = BC = a\sqrt 3 ,AC = a\)(Hình 99).

a) Tính góc giữa hai đường thẳng \(SA\) và \(BC\).

b) Tính góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\).

c) Tính số đo của góc nhị diện \(\left[ {B,SA,C} \right]\).

d) Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\).

e) Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\).

g) Tính thể tích của khối chóp \(S.ABC\).

Phương pháp:

a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)

Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).

Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\).

Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).

Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.

e) Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

g) Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải:

a) Do SA ⊥ (ABC) và BC ⊂ (ABC) nên SA ⊥ BC.

Vậy góc giữa hai đường thẳng SA và BC bằng 90°.

b) Vì SA ⊥ (ABC) nên AC là hình chiếu của SC trên (ABC).

Suy ra góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 

Do SA ⊥ (ABC) và AC ⊂ (ABC) nên SA ⊥ AC.

Xét tam giác SAC vuông tại A (do SA ⊥ AC) có:

Vậy góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°.

c) Do SA ⊥ (ABC) và AB, AC đều nằm trên (ABC).

Suy ra SA ⊥ AB, SA ⊥ AC.

Mà AB ∩ AC = A ∈ SA.

Vậy số đo của góc nhị diện [B, SA, C] bằng 60°.

d) Ta có: BC ⊥ SA (theo câu a);

               BC ⊥ AC;

               SA ∩ AC = A trong (SAC).

Suy ra BC ⊥ (SAC).

e) Ta có: AC ⊥ SA (theo câu c) và AC ⊥ BC.

Suy ra đoạn thẳng AC là đoạn vuông góc chung của hai đường thẳng SA và BC.

Khi đó d(SA, BC) = AC = a.

Vậy khoảng cách giữa hai đường thẳng SA và BC bằng a.

g) Diện tích tam giác ABC vuông tại C (do AC ⊥ BC) là:

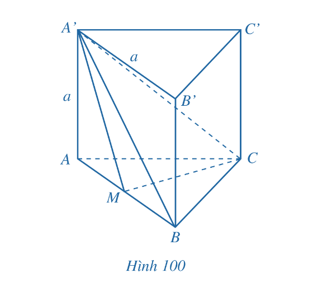
Bài 7 trang 117 SGK Toán 11 - Cánh Diều tập 2

Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(AB\) (Hình 100).

a) Tính góc giữa hai đường thẳng \(AB\) và \(B'C'\).

b) Tính góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\).

c) Tính số đo của góc nhị diện \(\left[ {B,CC',M} \right]\).

d) Chứng minh rằng \(CC'\parallel \left( {ABB'A'} \right)\). Tính khoảng cách giữa đường thẳng \(CC'\) và mặt phẳng \(\left( {ABB'A'} \right)\).

e) Chứng minh rằng \(CM \bot \left( {ABB'A'} \right)\). Tính khoảng cách giữa hai đường thẳng \(CC'\) và \(A'M\).

g) Tính thể tích của khối lăng trụ tam giác đều \(ABC.A'B'C'\) và thể tích khối chóp \(A'.MBC\).

Phương pháp:

a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)

Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).

Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\).

Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).

Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

d) ‒ Chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng song song với một đường thẳng nằm trên mặt phẳng.

‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.

e) ‒ Chứng minh đường thẳng vuông góc với mặt phẳng: Chứng minh đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trên mặt phẳng.

‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

g) ‒ Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).

‒ Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải:

Vì ABC.A’B’C’ là hình lăng trụ tam giác đều có tất cả các cạnh bằng a nên ta có:

⦁ Các mặt bên A’C’CA, B’C’CB, A’B’BA đều là hình vuông cạnh a.

⦁ Hai mặt đáy ABC và A’B’C’ là hai tam giác đều cạnh a và hai mặt phẳng chứa hai mặt đáy song song với nhau.

⦁ Các cạnh bên AA’, BB’, CC’ đều vuông góc với mặt phẳng đáy (ABC) và (A’B’C’).

a) Do B’C’CB là hình vuông nên BC // B’C’.

Vậy góc giữa hai đường thẳng AB và B’C’ bằng 60°.

b) Vì AA’ ⊥ (ABC) nên AB là hình chiếu của A’B trên (ABC).

Vậy góc giữa đường thẳng A’B và mặt phẳng (ABC) bằng 45°.

c) Do CC’ ⊥ (ABC) và BC, CM đều nằm trên (ABC).

Suy ra CC’ ⊥ BC, CC’ ⊥ CM.

Mà BC ∩ CM = C ∈ CC’.

Vậy số đo của góc nhị diện [B, CC, M] bằng 30°.

d) Do B’C’CB là hình vuông nên CC’ // BB’.

Mà BB’ ⊂ (ABB’A’) nên CC’ // (ABB’A’).

Khi đó d(CC’, (ABB’A’)) = d(C, (ABB’A’)).

Do AA’ ⊥ (ABC) và CM ⊂ (ABC) nên AA’ ⊥ CM.

Vì tam giác ABC đều có CM là đường trung tuyến nên đồng thời là đường cao của tam giác hay CM ⊥ AB.

Ta có: CM ⊥ AA’, CM ⊥ AB và AA’ ∩ AB = A trong (ABB’A’).

Suy ra CM ⊥ (ABB’A’).

Khi đó d(C, (ABB’A’)) = CM.

e) Theo câu d ta có CM ⊥ (ABB’A’).

Mà A’M ⊂ (ABB’A’) nên CM ⊥ A’M.

Do CC’ ⊥ (ABC) và CM ⊂ (ABC) nên CC’ ⊥ CM.

Ta thấy: CM ⊥ A’M, CM ⊥ CC’.

Suy ra đoạn thẳng CM là đoạn vuông góc chung của hai đường thẳng CC’ và A’M.

⦁ Vì A là hình chiếu của A’ trên (ABC) và (MBC) ≡ (ABC).

Suy ra A cũng là hình chiếu của A’ trên (MBC).

Nên ta có đoạn thẳng AA’ cũng là chiều cao của khối chóp A’.MBC.

Diện tích tam giác MBC vuông tại M là:

Bài 8 trang 117 SGK Toán 11 - Cánh Diều tập 2

Hình 101 là hình chụp đền Kukulcan, là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza, Mexico, được người Maya xây vào khoảng từ thế kỉ IX đến thế kỉ XII. Phần thân của đền, không bao gồm ngôi đền nằm phía trên, có dạng một khối chóp cụt tứ giác đều (không tính cầu thang và coi các mặt bên là phẳng) với độ dài đáy dưới là 55,3 m, chiều cao là 24 m, góc giữa cạnh bên và mặt phẳng đáy là khoảng \({47^ \circ }\).

(Nguồn: https://vi.wikipedia.org)

Tính thể tích phần thân ngôi đền có dạng khối chóp cụt tứ giác đều đó theo đơn vị mét khối (làm tròn kết quả đến hàng phần trăm).

Phương pháp:

Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'}  + S'} \right)\).

Lời giải:

Mô tả phần thân của đền Kukulcan trong bài toán bằng khối chóp cụt tứ giác đều ABCD.A’B’C’D’, với O và O’ lần lượt là tâm của hai đáy ABCD và A’B’C’D’.

Như vậy ta có:

⦁ ABCD là hình vuông cạnh 55,3 có diện tích S_ABCD = 55,3² = 3 058,09 (m²);

⦁ A’B’C’D’ là hình vuông;

⦁ Các cạnh bên A’A, B’B, C’C, D’D tạo với mặt đáy bằng 47°;

⦁ OO’ vuông góc với (ABCD) và (A’B’C’D’) và OO’ = 24 (m).

Do ABCD là hình vuông nên  do đó tam giác ABC vuông tại B.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

AC² = AB² + BC² = 55,3² + 55,3² = 2 . 55,3².

Dễ thấy: (ABCD) ∩ (A’C’CA) = AC;

              (A’B’C’D’) ∩ (A’C’CA) = A’C’.

Mà (ABCD) // (A’B’C’D’).

Suy ra AC // A’C’ hay A’C’CA là hình thang.

Xét hình thang A’C’CA, kẻ C’H ⊥ AC (H ∈ AC).

Vì OO’ ⊥ (ABCD) và AC ⊂ (ABCD) nên OO’ ⊥ AC.

Do đó C’H // OO’ (cùng vuông góc với AC).

Mà O’C’ // OH (do A’C’ // AC)

Suy ra O’C’HO là hình bình hành.

Do đó: C’H = OO’ = 24 (m) và OH = O’C’.

Vì OO’ ⊥ (ABCD) và OO’ // C’H nên C’H ⊥ (ABCD).

Suy ra CH là hình chiếu của CC’ trên (ABCD).

Suy ra tam giác A’B’C’ vuông cân tại B’.

Áp dụng định lí Pythagore trong tam giác A’B’C’ vuông cân tại B’ có:

A’B’² + B’C’² = A’C’² hay 2A’B’² = A’C’²

Diện tích hình vuông A’B’C’D’ cạnh 23,65 là: S _{A’B’C’D’} ≈ 23,65² = 559,3225 (m²).

Như vậy, thể tích khối chóp cụt tứ giác đều ABCD.A’B’C’D’ với chiều cao OO’ = 24 và diện tích hai đáy S_ABCD = 3 058,09; S_{A’B’C’D’} = 559,3225 là:

Vậy thể tích phần thân ngôi đền đã cho gần bằng 39 402,06 m³.

Sachbaitap.com