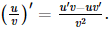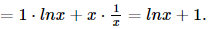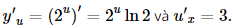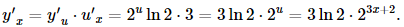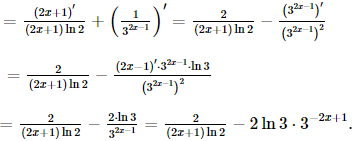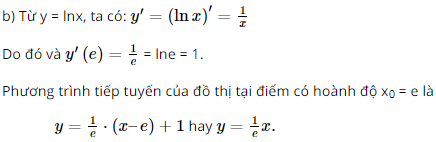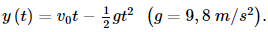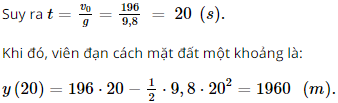Giải SGK Toán 11 Cánh Diều tập 2 trang 71, 72Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 71, 72 SGK Toán lớp 11 Cánh Diều tập 2.Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu ({v_0} = 196m/s) (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. (lấy (g = 9,8m/{s^2})) Bài 1 trang 71 SGK Toán 11 - Cánh Diều tập 2 a) \((u + v + w)' = u' + v' + w'\) b) \((u + v - w)' = u' + v' - w'\) c) \((uv)' = u'v'\) d) \(\left( {\frac{u}{v}} \right)' = \frac{{u'}}{{v'}};\,\,\,v = v(x) \ne 0,v' = v'(x) \ne 0\) Phương pháp: Dựa vào đạo hàm của các phép toán để xác định. Lời giải: Phát biểu đúng là: a), b). Phát biểu c) sai vì (uv)' = u'v + uv'. Phát biểu (d) sai vì Bài 2 trang 71 SGK Toán 11 - Cánh Diều tập 2 Cho \(u = u(x),\,v = v(x),\,w = w(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Chứng minh rằng \((u\,.\,v\,.\,w)' = u'\,.\,v\,.\,w + u\,.\,v'\,.\,w + u\,.\,v\,.\,w'\) Phương pháp: Dựa vào đạo hàm hợp và các tính chất để tính Lời giải: Đặt g = u . v và h = g . w. Khi đó h' = g' . w + g . w' = (uv)' . w + (uv) . w' = (u'v + uv') . w + (uv) . w' = u' . v . w + u . v' . w + u . v . w'. Bài 3 trang 71 SGK Toán 11 - Cánh Diều tập 2 Tìm đạo hàm của mỗi hàm số sau: a) \(y = 4{x^3} - 3{x^2} + 2x + 10\) b) \(y = \frac{{x + 1}}{{x - 1}}\) c) \(y = - 2x\sqrt x \) d) \(y = 3\sin x + 4\cos x - \tan x\) e) \(y = {4^x} + 2{e^x}\) f) \(y = x\ln x\) Phương pháp: Dựa vào các quy tắc tính đạo hàm để tính Lời giải: a) y' = (4x3)' – (3x2)' + (2x)' + (10)' = 4.3.x2 – 3.2.x + 2.1 = 12x2 – 6x + 2.
e) y' = (4x)' + (2ex)' = 4xln4 + 2ex. g) y' = (xlnx)' = (x)'.lnx + x.(lnx)' Bài 4 trang 71 SGK Toán 11 - Cánh Diều tập 2 Cho hàm số \(f(x) = {2^{3x + 2}}\) a) Hàm số f(x) là hàm hợp của hàm số nào? b) Tìm đạo hàm của f(x) Phương pháp: Dựa vào quy tắc đạo hàm và quy tắc hàm hợp để tính Lời giải: a) Đặt y = f(x) = 23x + 2 và u = 3x + 2, ta có y = 23x + 2 = 2u. Vậy y = f(x) = 23x + 2 là hàm hợp của 2 hàm số y = 2u, u = 3x + 2. b) Từ y = 2u và u = 3x + 2, ta có: Theo công thức tính đạo hàm của hàm hợp, ta có: Bài 5 trang 72 SGK Toán 11 - Cánh Diều tập 2 Tìm đạo hàm của mỗi hàm số sau: a) \(y = \sin 3x + {\sin ^2}x\) b) \(y = {\log _2}(2x + 1) + {3^{ - 2x + 1}}\) Phương pháp: Dựa vào quy tắc đạo hàm và quy tắc hàm hợp để tính. Lời giải: a)y'=(sin3x)' + (sin2x) = (3x)'.cos3x + 2(sinx)'.sinx = 3.cos3x + 2cosx.sinx = 3cos3x + sin2x. b) y' = (log2(2x + 1))' + (3−2x + 1)' ' Bài 6 trang 72 SGK Toán 11 - Cánh Diều tập 2 Viết phương trình tiếp tuyến của đồ thị hàm số sau: a) \(y = {x^3} - 3{x^2} + 4\) tại điểm có hoành độ \({x_0} = 2\) b) \(y = \ln x\) tại điểm có hoành độ \({x_0} = e\) c) \(y = {e^x}\) tại điểm có hoành độ \({x_0} = 0\) Phương pháp: Dựa vào phương trình tiếp tuyến đã học để làm bài. Lời giải: a) Từ y = x3 – 3x2 + 4, ta có: y' = (x3)' – (3x2)' + (4)' = 3x2 – 6x. Do đó y'(2) = 3.22 – 6.2 = 12 – 12 = 0. y(2) = 23 – 3.22 + 4 = 8 – 12 + 4 = 0. Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x0 = 2 là: y = 0(x – 2) + 0 = 0.
c) Từ y = ex, ta có: y' = (ex)' = ex. Do đó y'(0) = e0 = 1 và y(0) = e0 = 1. Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x0 = 0 là: y = 1(x – 0) +1 hay y = x + 1. Bài 7 trang 72 SGK Toán 11 - Cánh Diều tập 2 Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu \({v_0} = 196m/s\) (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. (lấy \(g = 9,8m/{s^2}\)) Phương pháp: Dựa vào công thức tính vận tốc để tìm thời điểm. Lời giải: Chọn gốc O là vị trí viên đạn được bắn lên. Phương trình chuyển động của viên đạn là:
Vận tốc tại thời điểm t là: v = y'(t) = v0 – gt (m/s). Do đó để v = 0 thì v0 – gt = 0 Bài 8 trang 72 SGK Toán 11 - Cánh Diều tập 2 Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích \({Q_0}\). Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức \(q(t) = {Q_0}\sin \omega t\), trong đó \(\omega \) là tốc độ góc. Biết rằng cường độ I(t) của dòng diện tại thời điểm t được tính theo công thức \(I(t) = q'(t)\). Cho biết \({Q_0} = {10^{ - 8}}(C)\) và \(\omega = {10^6}\pi \,\,\,(rad/s)\). Tính cường độ của dòng điện tại thời điểm \(t = 6(s)\) (tính chính xác đến \({10^{ - 5}}(mA)\)
Phương pháp: Dựa vào công thức đề bài cho để tìm đạo hàm sau đó tính. Lời giải: I(t) = q'(t) = (Q0sinωt)' = Q0ω.cosωt Cường độ của dòng điện tại thời điểm t = 6 (s) là: I(6) = 10–8 ∙106π.cos(106π.6) = 10–2π.cos0 = 0,01π (A). Sachbaitap.com
Xem thêm tại đây:
Bài 2. Các quy tắc tính đạo hàm
|
-

Giải SGK Toán 11 Cánh Diều tập 2 trang 75
Giải bài 1, 2, 3, 4, 5 trang 75 SGK Toán lớp 11 Cánh Diều tập 2. Một chất điểm chuyển động theo phương trình (s(t) = {t^3} - 3{t^2} + 8t + 1), trong đó t > 0, t tính bằng giây và s(t) tính bằng mét. Tìm vận tốc tức thời, gia tốc tức thời của chất diểm; a) Tại thời điểm t = 3(s) b) Tại thời điểm mà chất điểm di chuyển được 7 (m)

 Tải ngay
Tải ngay