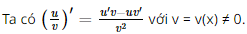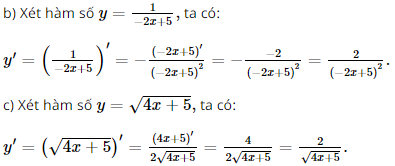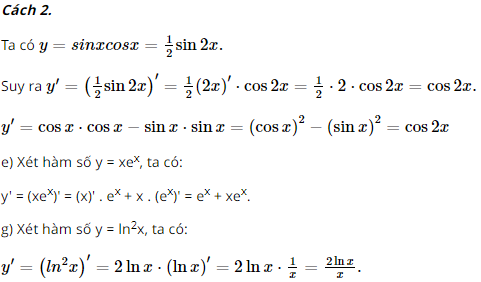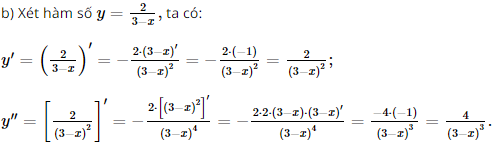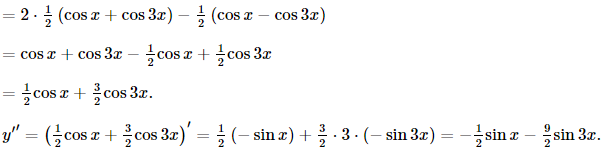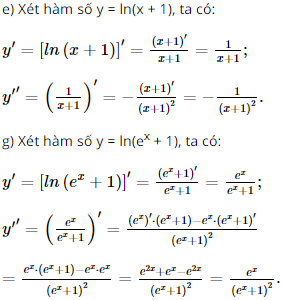Giải SGK Toán 11 Cánh Diều tập 2 trang 76Giải bài 1, 2, 3, 4, 5, 6 trang 76 SGK Toán lớp 11 Cánh Diều tập 2. Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức (v(t) = 2t + {t^2}), trong đó t > 0, t tính bằng giây và v(t) tính bằng m/s. Tìm gia tức thời của chất điểm: a) Tại thời điểm t = 3(s). b) Tại thời điểm mà vận tốc của chất điểm bằng 8 m/s Bài 1 trang 76 SGK Toán 11 - Cánh Diều tập 2 Cho \(u = u(x),v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng? A. \((uv)' = u'v'\) B. \((uv)' = uv'\) C. \((uv)' = u'v\) D. \((uv)' = u'v + uv'\) Phương pháp: Dựa vào công thức tính đạo hàm của phép nhân để rút ra đáp án. Lời giải: Đáp án đúng là: D Ta có: (uv)' = u'v + uv'. Bài 2 trang 76 SGK Toán 11 - Cánh Diều tập 2 Cho \(u = u(x),v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng? A. \(\left( {\frac{u}{v}} \right)' = \frac{{u'}}{{v'}}\) với \(v = v(x) \ne 0,v = v'(x) \ne 0\) B. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{v}\) với \(v = v(x) \ne 0\) C. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) với \(v = v(x) \ne 0\) D. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{v'}}\) với \(v = v(x) \ne 0;\,\,v' = v'(x) \ne 0\) Phương pháp: Dựa vào công thức tính đạo hàm của phép chia để rút ra đáp án. Lời giải: Đáp án đúng là: C
Bài 3 trang 76 SGK Toán 11 - Cánh Diều tập 2 Tính đạo hàm của mỗi hàm số sau: a) \(y = \left( {{x^2} + 2x} \right)\left( {{x^3} - 3x} \right)\) b) \(y = \frac{1}{{ - 2x + 5}}\) c) \(y = \sqrt {4x + 5} \) d) \(y = \sin x\cos x\) e) \(y = x{e^x}\) f) \(y = {\ln ^2}x\) Phương pháp: Dựa vào công thức đạo hàm của các hàm để tính. Lời giải: a) Xét hàm số y = (x2 + 2x)(x3 – 3x), ta có: y' = (x2 + 2x)'(x3 – 3x) + (x2 + 2x)(x3 – 3x)' = (2x + 2)(x3 – 3x) + (x2 + 2x)(3x2 – 3) = 2x4 – 6x2 + 2x3 – 6x + 3x4 – 3x2 + 6x3 – 6x = 5x4 + 8x3 – 9x2 – 12x. d) Xét hàm số y = sinxcosx Cách 1. y' = (sinxcosx)' = (sinx)'.cosx + sinx.(cosx)' = cosx.cosx + sinx.(–sinx) = cos2x – sin2x = cos2x.
Bài 4 trang 76 SGK Toán 11 - Cánh Diều tập 2 Tính đạo hàm cấp hai của mỗi hàm số sau: a) \(y = 2{x^4} - 3{x^3} + 5{x^2}\) b)\(y = \frac{2}{{3 - x}}\) c) \(y = \sin 2x\cos x\) d) \(y = {e^{ - 2x + 3}}\) e) \(y = \ln (x + 1)\) f) \(y = \ln ({e^x} + 1)\) Phương pháp: Dựa vào định nghĩa đạo hàm cấp hai để tính. Lời giải: a) Xét hàm số y = 2x4 – 3x3 + 5x2, ta có: y' = 8x3 – 9x2 + 10x; y'' = 24x2 – 18x + 10. c) Xét hàm số y = sin2xcosx, ta có: y' = (sin2xcosx)' = (sin2x)'.cosx + sin2x.(cosx)' = 2cos2x.cosx – sin2x.sinx d) Xét hàm số y = e–2x + 3, ta có: y' = (e–2x + 3)' = (–2x + 3)' . e–2x + 3 = –2e–2x+3; y'' = (–2e–2x+3)' = –2.(–2x + 3)'.e–2x+3 = 4e–2x+3. Bài 5 trang 76 SGK Toán 11 - Cánh Diều tập 2 Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức \(v(t) = 2t + {t^2}\), trong đó t > 0, t tính bằng giây và v(t) tính bằng m/s. Tìm gia tức thời của chất điểm: a) Tại thời điểm t = 3(s) b) Tại thời điểm mà vận tốc của chất điểm bằng 8 m/s Phương pháp: Dựa vào hàm số đạo hàm để tìm từng đại lượng sau đó thay số. Lời giải: Vận tốc của chất điểm chuyển động được biểu thị bởi công thức v(t) = t2 + 2t. a) Gia tốc tức thời của chất điểm: a(t) = v'(t) = 2t + 2. Gia tốc tức thời của chất điểm tại t = 3 (s) là: a(3) = 2 . 3 + 2 = 8 (m/s2). b) Để vận tốc của chất điểm bằng 8 m/s thì: t2 + 2t = 8 Suy ra t2 + 2t – 8 = 0 Do đó t = 2 (thỏa mãn) hoặc t = –4 (không thỏa mãn) Tại t = 2 thì a(2) = 2 . 2 + 2 = 6 (m/s2). Vậy tại thời điểm vận tốc của chất điểm bằng 8 m/s thì gia tốc tức thời là 6 m/s2. Bài 6 trang 76 SGK Toán 11 - Cánh Diều tập 2 Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động \(x = 4\cos \left( {\pi t - \frac{{2\pi }}{3}} \right) + 3\), trong đó t tính bằng giây và x tính bằng centimet a) Tìm vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm t (s) b) Tìm thời điểm mà vận tốc tức thời của con lắc bằng 0. Phương pháp: Dựa vào hàm số đạo hàm để tìm từng đại lượng sau đó thay số. Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 7
|

 Tải ngay
Tải ngay