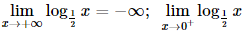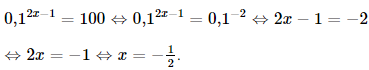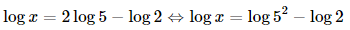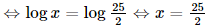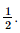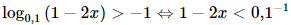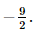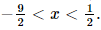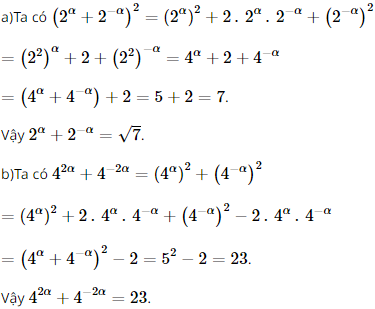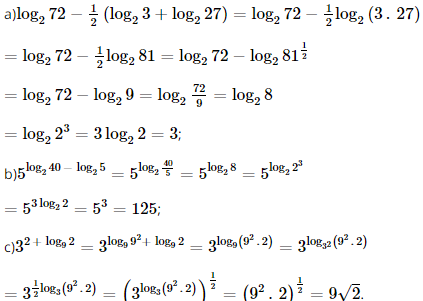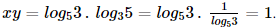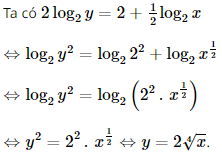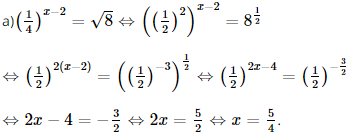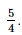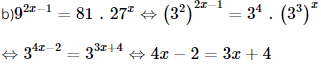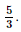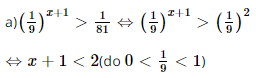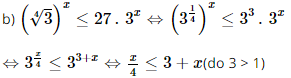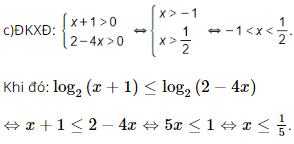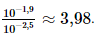Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 34, 35Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 34, 35 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện ra số lượng vi khuẩn tăng thêm 25% sau mỗi hai ngày. Bài 1 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Rút gọn biểu thức \({\left[ {{{\left( {\frac{1}{3}} \right)}^2}} \right]^{\frac{1}{4}}}.{\left( {\sqrt 3 } \right)^5}\), ta được A. \(\sqrt 3 \). B. \(3\sqrt 3 \). C. \(\frac{1}{{\sqrt 3 }}\). D. 9. Phương pháp: Sử dụng tính chất của luỹ thừa với số mũ hữu tỉ. Lời giải: Đáp án đúng là: D
Bài 2 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Nếu \({2^\alpha } = 9\) thì \({\left( {\frac{1}{{16}}} \right)^{\frac{\alpha }{8}}}\) có giá trị bằng A. \(\frac{1}{3}\). B. 3. C. \(\frac{1}{9}\). D. \(\frac{1}{{\sqrt 3 }}\). Phương pháp: Sử dụng tính chất của luỹ thừa, biến đổi \({\left( {\frac{1}{{16}}} \right)^{\frac{\alpha }{8}}}\) về dạng chứa \({2^\alpha }\). Lời giải: Đáp án đúng là: A
Bài 3 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Nếu \({a^{\frac{1}{2}}} = b\left( {a > 0,a \ne 1} \right)\) thì A. \({\log _{\frac{1}{2}}}a = b\). B. \(2{\log _a}b = 1\). C. \({\log _a}\frac{1}{2} = b\). D. \({\log _{\frac{1}{2}}}b = a\). Phương pháp: Sử dụng định nghĩa lôgarit: \({a^\alpha } = b \Leftrightarrow \alpha = {\log _a}b\). Lời giải: Đáp án đúng là: B
Bài 4 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Nếu \(x = {\log _3}4 + {\log _9}4\) thì \({3^x}\) có giá trị bằng A. 6. B. 8. C. 16. D. 64. Phương pháp: Sử dụng tính chất của lôgarit, đưa vế phải về lôgarit cơ số 3. Lời giải: Đáp án đúng là: B
⇔ 3x = 8. Bài 5 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho \(\alpha ,\beta \) là hai số thực với \(\alpha < \beta \). Khẳng định nào sau đây đúng? A. \({\left( {0,3} \right)^\alpha } < {\left( {0,3} \right)^\beta }\). B. \({\pi ^\alpha } \ge {\pi ^\beta }\). C. \({\left( {\sqrt 2 } \right)^\alpha } < {\left( {\sqrt 2 } \right)^\beta }\). D. \({\left( {\frac{1}{2}} \right)^\beta } > {\left( {\frac{1}{2}} \right)^\alpha }\). Phương pháp: Sử dụng tính chất của hàm số mũ. Lời giải: Đáp án đúng là: C • Xét phương án A. Do 0 < 0,3 < 1 nên hàm số y = 0,3x nghịch biến trên ℝ. Mà α < β nên (0,3)α < (0,3)β. • Xét phương án B. Do π > 1 nên hàm số y = πx đồng biến trên ℝ. Mà α < β nên πα < πβ. • Xét phương án C. Do Mà α < β nên • Xét phương án D. Do 0< Mà α < β nên Bài 6 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Hình nào vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\)?
Phương pháp: Dựa vào tính chất của đồ thị hàm số \(y = {\log _a}x\). Lời giải: Đáp án đúng là: D − Hàm số − Giới hạn: Bài 7 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Phương trình \(0,{1^{2{\rm{x}} - 1}} = 100\) có nghiệm là: A. \( - \frac{1}{2}\). B. \(\frac{1}{3}\). C. \(1\frac{1}{2}\). D. \(2\frac{1}{3}\). Phương pháp: Đưa 2 vế của phương trình về cùng cơ số. Lời giải: Đáp án đúng là: A
Bài 8 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Tập nghiệm của bất phương trình \(0,{5^{3{\rm{x}} - 1}} > 0,25\) là A. \(\left( { - \infty ;1} \right)\). B. \(\left( {1; + \infty } \right)\). C. \(\left( {0;1} \right)\). D. \(\left( { - \infty ; - \frac{1}{3}} \right)\). Phương pháp: Đưa 2 vế của bất phương trình về cùng cơ số. Lời giải: Đáp án đúng là: A 0,53x−1>0,25⇔0,53x−1>0,52 ⇔3x−1<2(do 0<0,5<1) ⇔3x<3⇔x<1. Vậy tập nghiệm của bất phương trình là (−∞;1). Bài 9 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Nếu \(\log x = 2\log 5 - \log 2\) thì A. \(x = 8\). B. \(x = 23\). C. \(x = 12,5\). D. \(x = 5\). Phương pháp: Bước 1: Tìm ĐKXĐ. Bước 2: Đưa 2 vế của phương trình về cùng cơ số và giải phương trình. Bước 3: Kết luận. Lời giải: Đáp án đúng là: C ĐKXĐ: x > 0 Khi đó:
Bài 10 trang 34 SGK Toán 11 - Chân trời sáng tạo tập 2 Số nguyên \(x\) nhỏ nhất thoả mãn \({\log _{0,1}}\left( {1 - 2x} \right) > - 1\) là A. \(x = 0\). B. \(x = 1\). C. \(x = - 5\). D. \(x = - 4\). Phương pháp:Bước 1: Tìm ĐKXĐ.
Bước 2: Đưa 2 vế của phương trình về cùng cơ số và giải phương trình. Bước 3: Kết luận. Lời giải: Đáp án đúng là: D ĐKXĐ: 1−2x>0⇔x< Khi đó: ⇔1−2x<10⇔−2x<9⇔x> Kết hợp với điều kiện ta được nghiệm của bất phương trình là Vậy số nguyên \(x\) nhỏ nhất thoả mãn \({\log _{0,1}}\left( {1 - 2x} \right) > - 1\) là là x = − 4. Bài 11 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Biết \({4^\alpha } + {4^{ - \alpha }} = 5\). Vậy số nguyên x nhỏ nhất thỏa mãn Tính giá trị của các biểu thức: a) \({2^\alpha } + {2^{ - \alpha }}\); b) \({4^{2\alpha }} + {4^{ - 2\alpha }}\). Phương pháp: Sử dụng hằng đẳng thức để biến đổi nhằm xuất hiện \({4^\alpha } + {4^{ - \alpha }}\) Lời giải:
Bài 12 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Tính giá trị của các biểu thức: a) \({\log _2}72 - \frac{1}{2}\left( {{{\log }_2}3 + {{\log }_2}27} \right)\); b) \({Sử dụng tính chất của lôgarit.5^{{{\log }_2}40 - {{\log }_2}5}}\); c) \({3^{2 + {{\log }_9}2}}\). Phương pháp: Sử dụng tính chất của lôgarit. Lời giải:
Bài 13 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Biết rằng \({5^x} = 3\) và \({3^y} = 5\). Không sử dụng máy tính cầm tay, tính giá trị của \(xy\). Phương pháp: Sử dụng định nghĩa lôgarit, tìm \(x,y\) sau đó sử dụng công thức đổi cơ số để tính \(xy\). Lời giải: Ta có 5x = 3 ⇔ x = log5 3 và 3y = 5 ⇔ y = log3 5. Do đó Bài 14 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Viết công thức biểu thị \(y\) theo \(x\), biết \(2{\log _2}y = 2 + \frac{1}{2}{\log _2}x\). Phương pháp: Sử dụng tính chất của lôgarit Lời giải:
Bài 15 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Giải các phương trình sau: a) \({\left( {\frac{1}{4}} \right)^{x - 2}} = \sqrt 8 \); b) \({9^{2x - 1}} = {81.27^x}\); c) \(2{\log _5}\left( {x - 2} \right) = {\log _5}9\); d) \({\log _2}\left( {3{\rm{x}} + 1} \right) = 2 - {\log _2}\left( {x - 1} \right)\). Phương pháp: Đưa 2 vế của phương trình về cùng cơ số. Lời giải:
Vậy phương trình đã cho có nghiệm x=54">x=54">x=
Vậy phương trình đã cho có nghiệm x = 6. c) ĐKXĐ: x – 2 > 0 ⇔ x > 2. Khi đó:
Vậy phương trình đã cho có nghiệm x = 5.
Vậy phương trình đã cho có nghiệm x= Bài 16 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Giải các bất phương trình: a) \({\left( {\frac{1}{9}} \right)^{x + 1}} > \frac{1}{{81}}\); b) \({\left( {\sqrt[4]{3}} \right)^x} \le {27.3^x}\); c) \({\log _2}\left( {x + 1} \right) \le {\log _2}\left( {2 - 4{\rm{x}}} \right)\). Phương pháp: Đưa 2 vế của bất phương trình về cùng cơ số. Lời giải:
⇔x<1 Vậy bất phương trình đã cho có nghiệm x < 1
⇔x≥− 4">⇔x≥−4. Vậy bất phương trình đã cho có nghiệm x≥− 4">x≥−4.
Kết hợp với điều kiện ta được nghiệm của bất phương trình −1<x≤ Bài 17 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện ra số lượng vi khuẩn tăng thêm 25% sau mỗi hai ngày. a) Công thức \(P\left( t \right) = {P_0}.{a^t}\) cho phép tính số lượng vi khuẩn của mẻ nuôi cấy sau \(t\) ngày kể từ thời điểm ban đầu. Xác định các tham số \({P_0}\) và \(a\left( {a > 0} \right)\). Làm tròn \(a\) đến hàng phần trăm. b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu? Làm tròn kết quả đến hàng trăm. c) Sau bao nhiêu ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu? Làm tròn kết quả đến hàng phần mười. Phương pháp: a) Thay \({P_0} = 1000,P\left( t \right) = 125\% {P_0},t = 2\) vào công thức \(P\left( t \right) = {P_0}.{a^t}\). b) Thay \(t = 5\) vào công thức \(P\left( t \right) = {P_0}.{a^t}\). c) Thay \(P\left( t \right) = 2{P_0}\) vào công thức \(P\left( t \right) = {P_0}.{a^t}\). Lời giải: a) Ban đầu có 1000 vi khuẩn nên P0=1000. Sau 2 ngày, số lượng vi khuẩn là: P=125% . P0=125%.1000=1250 Ta có:P(2)=P0.a2⇔1250=1000.a2 ⇔a2=1,25⇔a≈1,12. b) Số lượng vi khuẩn sau 5 ngày là: P(5)=P0.a5=1000.1,122≈1800(vi khuẩn). c) Với P(t)=2P0, ta có: P(t)=P0.at⇔2P0=P0.1,12t ⇔1,12t=2⇔t=log1,122≈6,1(ngày) Vậy sau 6,1 ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu. Bài 18 trang 35 SGK Toán 11 - Chân trời sáng tạo tập 2 Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức \(pH = - \log \left[ {{H^ + }} \right]\), trong đó [H+] là nồng độ H+ của dung dịch đó tính bằng mol/L. Nồng độ H+ trong dung dịch cho biết độ acid của dung dịch đó. a) Dung dịch acid A có độ pH bằng 1,9; dung dịch acid B có độ pH bằng 25. Dung dịch nào có độ acid cao hơn và cao hơn bao nhiêu lần? b) Nước cất có nồng độ H+ là 10 mol/L. Nước chảy ra từ một vòi nước có độ pH từ 6,5 đến 6,7 thì có độ acid cao hay thập hơn nước cất? Phương pháp: a) Tính nồng độ acid của 2 dung dịch và so sánh. b) Giải bất phương trình \(6,5 < pH < 6,7\). Lời giải: a)• pHA=1,9⇔−log[H+]=1,9 ⇔log[H+]=−1,9⇔H+=10−1,9. Vậy độ acid của dung dịch A là 10−1,9 mol/L. • pHB=2,5⇔−log[H+]=2,5 ⇔log[H+]=−2,5⇔H+=10−2,5. Vậy độ acid của dung dịch B là 10−2,5mol/L. Ta có: Vậy độ acid của dung dịch A cao hơn độ acid của dung dịch B 3,98 lần. b) Ta có:6,5<pH<6,7⇔6,5<−log[H+]<6,7 ⇔−6,5>log[H+]>−6,7⇔10−6,5>H+>10−6,7. Do đó nước chảy từ vòi nước có độ acid từ 10−6,7mol/L đến 10−6,5mol/L. Vậy nước đó có độ acid cao hơn nước cất. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 6
|

 Tải ngay
Tải ngay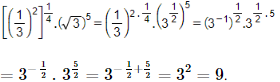
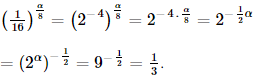
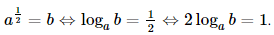
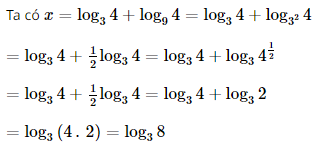
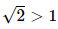 nên hàm số
nên hàm số 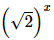
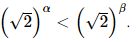
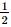
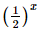
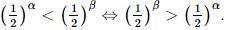
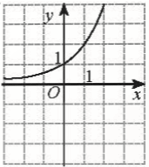
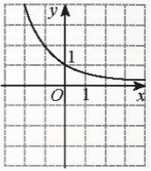
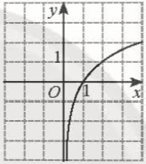
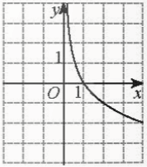
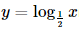 nghịch biến trên (0; +∞). Loại A, C.
nghịch biến trên (0; +∞). Loại A, C.