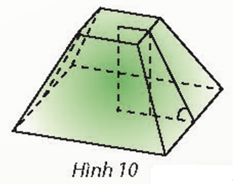
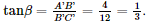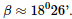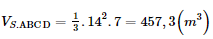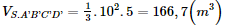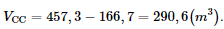Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 85Giải bài 1, 2, 3, 4, 5 trang 85 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm. Bài 1 trang 85 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho tứ diện đều \(ABCD\). Vẽ hình bình hành \(BCED\). a) Tìm góc giữa đường thẳng \(AB\) và \(\left( {BCD} \right)\). b) Tim góc phẳng nhị diện \(\left[ {A,CD,B} \right];\left[ {A,CD,E} \right]\). Phương pháp: ‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. ‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a'\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a'} \right)\). Lời giải:
a) Gọi I là trung điểm của CD, O là tâm của ΔBCD. ⇒ AO ⊥ (BCD) ⇒ (AB, (BCD)) = (AB, OB) = Vậy góc giữa đường thẳng AB và (BCD) là b) • ΔACD đều nên AI ⊥ CD • ΔBCD đều nên BI ⊥ CD Do đó [A, CD, B]=ˆAIB[A, CD, B]= Vậy • ΔACD đều nên AI ⊥ CD • ΔECD đều nên EI ⊥ CD Do đó [A, CD, E] = Vậy Bài 2 trang 85 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và có tất cả các cạnh bằng nhau. a) Tìm góc giữa đường thẳng \(SA\) và \(\left( {ABCD} \right)\). b) Tim góc phẳng nhị diện \(\left[ {A,SO,B} \right];\left[ {S,AB,O} \right]\). Phương pháp: ‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. ‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a'\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a'} \right)\). Lời giải:
a) S.ABCD là hình chóp tứ giác đều có O là tâm của đáy ⇒ SO ⊥ (ABCD) ⇒ (SA, (ABCD)) = (SA,OA) = Vậy góc giữa đường thẳng SA và (ABCD) là b) Gọi M là trung điểm của AB SO ⊥ (ABCD) ⇒ SO ⊥ AO, SO ⊥ BO Vậy AOB là góc phẳng nhị diện [A, SO, B] • ABCD là hình vuông nên • ΔSAB đều nên SM ⊥ AB • ΔOAB vuông cân tại O nênOM ⊥ AB Vậy Bài 3 trang 85 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp cụt lục giác đều \(ABCDEF.A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\) a) Tìm góc giữa cạnh bên và mặt đáy. b) Tìm góc phẳng nhị diện \(\left[ {O,AB,A'} \right];\left[ {O',A'B',A} \right]\). Phương pháp: ‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. ‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với , gọi \(a,a'\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a'} \right)\). Lời giải:
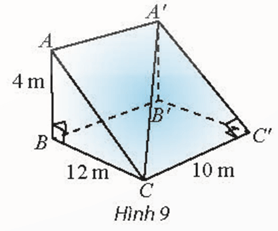
a) Kẻ C′H ⊥ OC (H OC). OO′C′H là hình chữ nhật nên OO′// C′H. Mà OO′ ⊥ (ABCDEF) nên C′H ⊥ (ABCDEF). Do đó (CC′, (ABCDEF)) = (CC′, CH) = b) Gọi M, M′ lần lượt là trung điểm của AB, A′B′. Khi đó, OM ⊥ AB, O′M′ ⊥ A′B. ABB′A′ là hình thang cân nên MM′ ⊥ AB, MM′ ⊥ A′B. Do đó [O, AB, A′] = Bài 4 trang 85 SGK Toán 11 - Chân trời sáng tạo tập 2 Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9. a) Tính số đo góc giữa đường thẳng \(CA'\) và . b) Tính số đo góc nhị diện cạnh \(CC'\).
Phương pháp: ‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. ‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\) Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\). Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\). Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\). Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\). Lời giải: a) Xét tam giác vuông CBB′ có: Gọi là góc giữa đường thẳng (CA′, (CC′B′B)) = Khi đó: Suy ra α≈ 14°22'. b) Ta có: CC′ ⊥ (ABC) ⇒ CC′ ⊥ AC, CC′ ⊥ BC. Gọi là góc phẳng nhị diện cạnh [A’, CC’, B’] =
Suy ra Bài 5 trang 85 SGK Toán 11 - Chân trời sáng tạo tập 2 Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
Phương pháp: ‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\) Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\). Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\). Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\). Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\). ‒ Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\). Lời giải: Vì ABCD là hình vuông nên ta có OF = 7m Chiều cao khối chóp S.ABCD là: Tuơng tự có chiều cao khối chóp S.A′B′C′D′ là: SO′ = 5m Thể tích khối chóp S.ABCD: Thể tích khối chóp S.A’B’C’D’: Thể tích khối chóp cụt bằng số khối đất phải đào: Vậy có 290,6 m3 khối đất cần phải di chuyển ra khỏi hầm. Sachbaitap.com
Xem thêm tại đây:
Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
|
-

Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 86, 87
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 trang 86, 87 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Cho hình hộp (ABCD.A'B'C'D') có cạnh bên (AA' = a), đáy (ABCD) là hình thoi có (AB = BD = a). Hình chiếu vuông góc của (A') lên mặt đáy trùng với điểm (O) là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp.

 Tải ngay
Tải ngay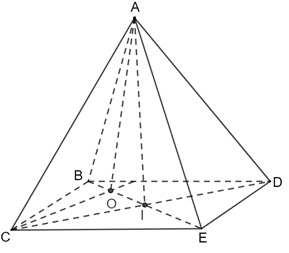
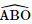
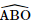 .
.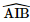
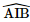 là góc phẳng nhị diện [A, CD, B].
là góc phẳng nhị diện [A, CD, B].
 là góc phẳng nhị diện [A,CD, E].
là góc phẳng nhị diện [A,CD, E].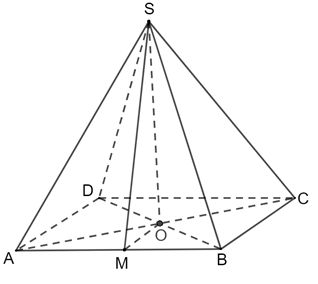
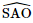
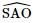

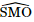 là góc phẳng nhị diện [S, AB, O].
là góc phẳng nhị diện [S, AB, O].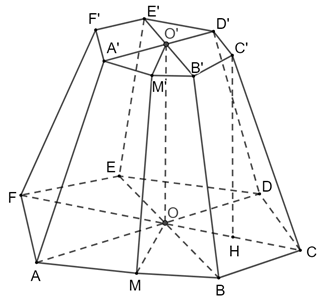
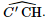 .
.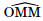 ; [O′, A′B′, A] =
; [O′, A′B′, A] = 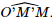
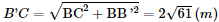
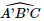
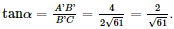 .
.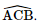 .
.