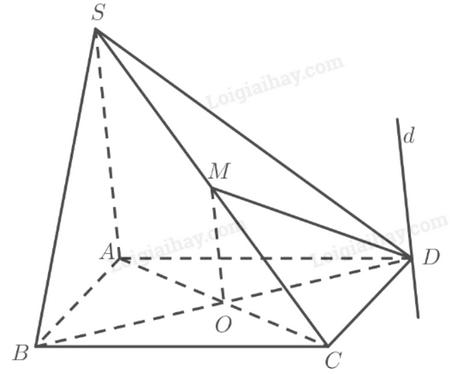
Giải SGK Toán 11 trang 111, 112 Chân trời sáng tạo tập 1

Bài 1 trang 111 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm hai đường chéo. Cho \(M\) là trung điểm của \(SC\).

a) Chứng minh đường thẳng \(OM\) song song với hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBA} \right)\);

b) Tìm giao tuyến của hai mặt phẳng \(\left( {OMD} \right)\) và \(\left( {SAD} \right)\).

Lời giải:

a) \(M\) là trung điểm của \(SC\)

\(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)

\( \Rightarrow OM\) là đường trung bình của tam giác \(SAC\)

\(\left. \begin{array}{l} \Rightarrow OM\parallel SA\\SA \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SA{\rm{D}}} \right)\)

Ta có:

\(\left. \begin{array}{l}OM\parallel SA\\SA \subset \left( {SBA} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SBA} \right)\)

b) Ta có:

\(\left. \begin{array}{l}D \in \left( {OM{\rm{D}}} \right) \cap \left( {SA{\rm{D}}} \right)\\OM \subset \left( {OM{\rm{D}}} \right)\\SA \subset \left( {SA{\rm{D}}} \right)\\OM\parallel SA\end{array} \right\}\)

\( \Rightarrow \) Giao tuyến của hai mặt phẳng \(\left( {OMD} \right)\) và \(\left( {SAD} \right)\) là đường thẳng \(d\) đi qua điểm \(D\), song song với \(OM\) và \(SA\).

Bài 2 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của \(ABCD\) và \(ABEF\).

a) Chứng minh đường thẳng \(OO'\) song song với các mặt phẳng \(\left( {CDF{\rm{E}}} \right),\left( {ADF} \right)\) và \(\left( {BCE} \right)\).

b) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AF\) và \(BE\). Chứng minh \(MN\parallel \left( {CDF{\rm{E}}} \right)\).

c) Tìm giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\).

Phương pháp:

– Để chứng minh đường thẳng song song với mặt phẳng, ta chứng minh đường thẳng đấy không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng.

‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:

+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.

+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.

Lời giải:

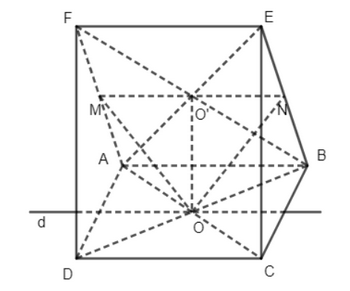
a) Vì O là tâm hình bình hành ABCD nên O là trung điểm AC và BD, O’ là tâm của hình bình hành ABEF nên O’ là trung điểm AE và BF.

+) Ta có: OO’ // FD (tính chất đường trung bình trong tam giác BDF), mà FD ⊂ (CDEF). Do đó OO’ // (CDEF).

+) Ta lại có: FD ⊂ (ADF) nên OO’ // (ADF).

+) Ta có: OO’ // EC (tính chất đường trung bình trong tam giác ACE), mà EC ⊂ (BCE). Do đó OO’ // (BCE).

b) Vì M và N lần lượt là trung điểm của AF và BE nên MN là đường trung bình của ABEF, suy ra MN // EF mà EF ⊂ (CDEF). Do đó MN // (CDEF).

c) Ta có MN // AB mà AB ⊂ (ABCD) và MN ⊂ (OMN)

Ta lại có: O ∈ (OMN) ∩ (ABCD)

Do đó giao tuyến của (OMN) và (ABCD) là đường thẳng đi d qua O và song song với AB.

Bài 3 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và một điểm \(M\) di động trên cạnh \(AD\). Một mặt phẳng \(\left( \alpha  \right)\) qua \(M\), song song với \(C{\rm{D}}\) và \(SA\), cắt \(BC,SC,SD\) lần lượt tại \(N,P,Q\).

a) \(MNPQ\) là hình gì?

b) Gọi \(I = MQ \cap NP\). Chứng minh rằng \(I\) luôn luôn thuộc một đường thẳng cố định khi \(M\) di động trên \(AD\).

Phương pháp:

Áp dụng định lí 2 về giao tuyến của ba mặt phẳng: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Lời giải:

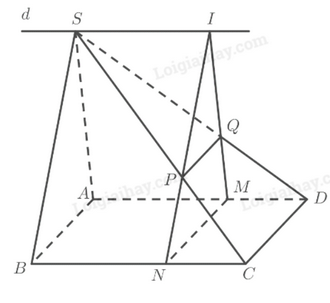
a) Ta có:

\(\begin{array}{l}MN = \left( \alpha  \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha  \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).

\( \Rightarrow MNPQ\) là hình bình hành.

b) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).

Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).

Bài 4 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha  \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha  \right)\) với các cạnh \(AC,CD\) và \(DB\).

a) Chứng minh \(MNPQ\) là hình bình hành.

b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?

Phương pháp:

Áp dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Lời giải:

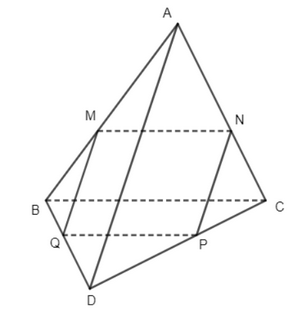
a) Trong mặt phẳng (ABC) từ điểm M kẻ đường thẳng song song với BC cắt AC tại N.

Trong mặt phẳng (ACD) từ điểm N kẻ đường thẳng song song với AD cắt cạnh CD tại P.

Trong mặt phẳng (BCD) từ điểm P kẻ đường thẳng song song với BC cắt cạnh BD tại Q.

Nối M với Q lại ta được mặt phẳng (MNPQ) chính là mặt phẳng (α) cần dựng.

Xét tứ giác MNPQ, có:

MN // QP (cùng // BC)

MQ // NP (cùng //AD)

Do đó tứ giác MNPQ là hình bình hành (theo dấu hiệu nhận biết).

b) Để tứ giác MNPQ là hình thoi thì MN = NP, điều này xảy ra trong trường hợp M là trung điểm của AB và AD = BC.

Bài 5 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB\). Gọi \(M\) là trung điểm của \(CD\), \(\left( P \right)\) là mặt phẳng qua \(M\) song song với \(SA\) và \(BC\). Tìm giao tuyến của \(\left( P \right)\) với các mặt của hình chóp \(S.ABCD\).

Phương pháp:

Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:

+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.

+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.

Lời giải:

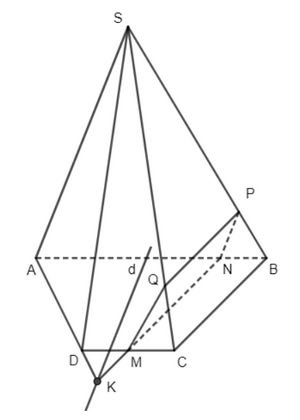
+) Giao tuyến của (P) và (ABCD):

Từ điểm M kẻ đường thẳng song song với BC cắt AB tại N

Suy ra giao tuyến của (P) và (ABCD) là MN.

+) Giao tuyến của (P) và (SAB):

Từ điểm N kẻ đường thẳng song song với SA cắt SB tại P

Suy ra giao tuyến của (P) và (SAB) là NP.

+) Giao tuyến của (P) và (SBC):

Từ điểm P kẻ đường thẳng song song với BC cắt SC tại Q

Suy ra giao tuyến của (P) và (SBC) là PQ.

+) Giao tuyến của (P) và (SDC) là MQ.

+) Giao tuyến của (P) và (SAD):

Kéo dài MN cắt AD tại K, từ K kẻ đường thẳng d song song với SA.

Suy ra giao tuyến (P) và (SAD) là d.

Bài 6 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo

Mô tả vị trí tương đối của các đường thẳng \(a,b,c,d,e\) với mặt phẳng \(\left( P \right)\) là mặt trước của toà nhà (Hình 19).

Phương pháp:

Dựa vào số điểm chung của đường thẳng và mặt phẳng.

Lời giải:

Ta có: \(a \subset \left( P \right),b\parallel \left( P \right),c\parallel \left( P \right),d\) cắt \(\left( P \right),e \subset \left( P \right)\)

Sachbaitap.com