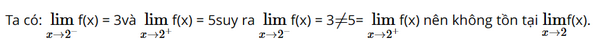Giải SGK Toán 11 trang 72 Cánh Diều tập 1Giải bài 1, 2, 3, 4, 5, 6 trang 72 SGK Toán lớp 11 Cánh Diều tập 1. Bài 1. Sử dụng định nghĩa, tìm các giới hạn sau: Bài 1 trang 72 SGK Toán 11 tập 1 - Cánh Diều Sử dụng định nghĩa, tìm các giới hạn sau: a) \(\mathop {\lim }\limits_{x \to - 3} {x^2};\) b) \(\mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}}.\) Phương pháp: Sử dụng định nghĩa giới hạn hữu hạn của hàm số tại một điểm Cho khoảng K chứa điểm \({x_0}\) và hàm số \(f(x)\) xác định trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\). Hàm số \(f(x)\) có giới hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\) Lời giải: a) \(\mathop {\lim }\limits_{x \to - 3} {x^2};\) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \(\lim {x_n} = - 3.\) Ta có \(\lim x_n^2 = {\left( { - 3} \right)^2} = 9\) Vậy \(\mathop {\lim }\limits_{x \to - 3} {x^2} = 9.\) b) \(\mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}}.\) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \(\lim {x_n} = 5.\) Ta có \(\lim \frac{{{x_n}^2 - 25}}{{{x_n} - 5}} = \lim \frac{{\left( {{x_n} - 5} \right)\left( {{x_n} + 5} \right)}}{{{x_n} - 5}} = \lim \left( {{x_n} + 5} \right) = \lim {x_n} + 5 = 5 + 5 = 10\) Vậy \(\mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}} = 10.\) Bài 2 trang 72 SGK Toán 11 tập 1 - Cánh Diều Biết rằng hàm số \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 3\) và \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 5.\) Trong trường hợp này có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\) hay không? Giải thích. Phương pháp: \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L\) Lời giải:
Bài 3 trang 72 SGK Toán 11 tập 1 - Cánh Diều Tính các giới hạn sau: a) \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 4x + 3} \right);\) b) \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 5x + 6}}{{x - 3}};\) c) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x - 1}}{{x - 1}}.\) Phương pháp: Sử dụng định lí về phép toán trên giới hạn hữu hạn của hàm số Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\)\(\left( {L,M \in \mathbb{R}} \right)\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\) \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\) \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\) Nếu \(f(x) \ge 0\) với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \). Lời giải: a) \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to 2} {x^2} - \mathop {\lim }\limits_{x \to 2} \left( {4x} \right) + 3 = {2^2} - 4.2 + 3 = - 1\) b) \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 5x + 6}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{\left( {x - 3} \right)\left( {x - 2} \right)}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \left( {x - 2} \right) = \mathop {\lim }\limits_{x \to 3} x - 2 = 3 - 2 = 1\) c) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt x + 1}} = \frac{1}{{\sqrt 1 + 1}} = \frac{1}{2}\) Bài 4 trang 72 SGK Toán 11 tập 1 - Cánh Diều Tính các giới hạn sau: a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{9x + 1}}{{3x - 4}};\) b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{7x - 11}}{{2x + 3}};\) c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{x};\) d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{x};\) e) \(\mathop {\lim }\limits_{x \to {6^ - }} \frac{1}{{x - 6}};\) g) \(\mathop {\lim }\limits_{x \to {7^ + }} \frac{1}{{x - 7}}.\) Phương pháp: - Sử dụng định lí về phép toán trên giới hạn hữu hạn của hàm số. - Sử dụng giới hạn cơ bản sau: \(\mathop {\lim }\limits_{x \to {a^ + }} \frac{1}{{x - a}} = + \infty ;\mathop {\lim }\limits_{x \to {a^ - }} \frac{1}{{x - a}} = - \infty \) Lời giải:
Bài 5 trang 72 SGK Toán 11 tập 1 - Cánh Diều Một công ty sản xuất máy tính đã xác định được rằng, tính trung bình một nhân viên có thể lắp ráp được \(N\left( t \right) = \frac{{50t}}{{t + 4}}\,\,\left( {t \ge 0} \right)\) bộ phận mỗi ngày sau t ngày đào tạo. Tính \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\) và cho biết ý nghĩa của kết quả. Phương pháp: Tính giới hạn bằng phương pháp chia cả tử và mẫu cho \({t^n}\), với n là số mũ cao nhất trong biểu thức. Lời giải: \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{50t}}{{t + 4}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{50t}}{{t\left( {1 + \frac{4}{t}} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{50}}{{1 + \frac{4}{t}}} = \frac{{50}}{{1 + 0}} = 50\) Vậy khi số ngày đào tạo càng nhiều thì số bộ phận mà trung bình một nhân viên có thể lắp ráp được mỗi ngày tối đa 50 bộ phận. Bài 6 trang 72 SGK Toán 11 tập 1 - Cánh Diều Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50 000 + 105x. a) Tính chi phí trung bình \(\overline C \left( x \right)\) để sản xuất một sản phẩm. b) Tính \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right)\) và cho biết ý nghĩa của kết quả. Phương pháp: Tính giới hạn bằng phương pháp chia cả tử và mẫu cho \({x^n}\), với n là số mũ cao nhất trong biểu thức. Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài 2. Giới hạn của hàm số
|
-

Giải SGK Toán 11 trang 77 Cánh Diều tập 1
Giải bài 1, 2, 3, 4, 5, 6 trang 77 SGK Toán lớp 11 Cánh Diều tập 1. Bài 4. Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

 Tải ngay
Tải ngay