Giải SGK Toán 11 trang 79, 80 Cánh Diều tập 1

Bài 1 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\) và \({x_0} \in (a;b)\). Điều kiện cần và đủ để hàm số \(y = f(x)\) liên tục tại \({x_0}\) là:

A. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = f\left( {{x_0}} \right)\).                                    

B. \(\mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).

C. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x)\).                              

D. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).

Phương pháp:

Định nghĩa hàm số liên tục tại một điểm.

Cho hàm \(y = f(x)\) xác định trên khoảng \(\left( {a;b} \right)\), \({x_0} \in \left( {a;b} \right)\). Hàm số \(f(x)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).

\(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\)

Lời giải:

Theo lí thuyết ta chọn đáp án D.

Bài 2 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Tính các giới hạn sau:

a) \(\lim \frac{{2{n^2} + 6n + 1}}{{8{n^2} + 5}}\)                            

b) \(\lim \frac{{4{n^2} - 3n + 1}}{{ - 3{n^3} + 5{n^2} - 2}}\);          

c) \(\lim \frac{{\sqrt {4{n^2} - n + 3} }}{{8n - 5}}\);

d) \(\lim \left( {4 - \frac{{{2^{n + 1}}}}{{{3^n}}}} \right)\)                           

e) \(\lim \frac{{{{4.5}^n} + {2^{n + 2}}}}{{{{6.5}^n}}}\)                         

g) \(\lim \frac{{2 + \frac{4}{{{n^3}}}}}{{{6^n}}}\).

Phương pháp:

Sử dụng phương pháp:

Chia cả tử và mẫu cho \({x^n}\), với n là số mũ cao nhất trong biểu thức đối với câu a, b, c.

Chia cả tử và mẫu cho \({a^n}\), với a là cơ số lớn nhất trong biểu thức đối với câu d, e.

Sử dụng giới hạn của một tích đối với câu g.

Lời giải:

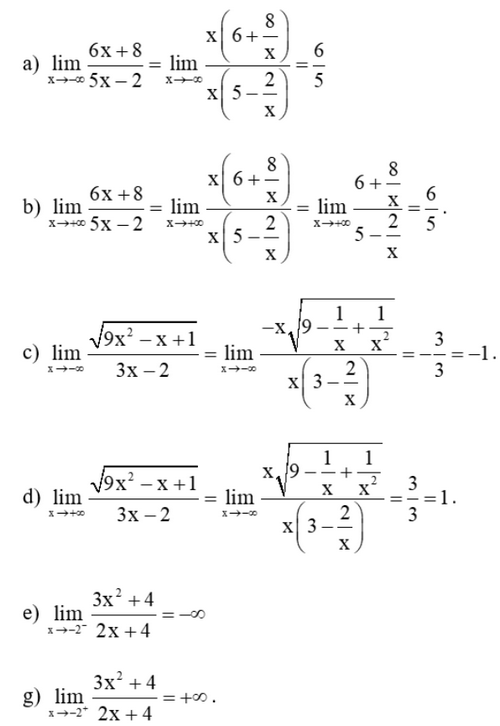
Bài 3 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Tính các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - 3} \left( {4{x^2} - 5x + 6} \right)\);           

b) \(\mathop {\lim }\limits_{x \to 2} \frac{{2{x^2} - 5x + 2}}{{x - 2}}\);                  

c) \(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x  - 2}}{{{x^2} - 16}}\).

Phương pháp:

Sử dụng định lí về phép toán trên giới hạn hữu hạn của hàm số

\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0};\mathop {\lim }\limits_{x \to {x_0}} c = c\)

Đối với câu b,c (dạng \(\frac{0}{0}\)): phân tích đa thức thành nhân tử để triệt tiêu giới hạn dạng \(\frac{0}{0}\).

Lời giải:

a) \(\mathop {\lim }\limits_{x \to  - 3} \left( {4{x^2} - 5x + 6} \right) = 4.{\left( { - 3} \right)^2} - 5.\left( { - 3} \right) + 6 = 57\)

b) \(\mathop {\lim }\limits_{x \to 2} \frac{{2{x^2} - 5x + 2}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right)\left( {2x - 1} \right)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \left( {2x - 1} \right) = 2.2 - 1 = 3\)

c) \(\begin{array}{c}\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x  - 2}}{{{x^2} - 16}} = \mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x  - 2}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = \mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)\left( {x + 4} \right)}} = \mathop {\lim }\limits_{x \to 4} \frac{1}{{\left( {\sqrt x  + 2} \right)\left( {x + 4} \right)}}\\ = \frac{1}{{\left( {\sqrt 4  + 2} \right)\left( {4 + 4} \right)}} = \frac{1}{{32}}\end{array}\)

Bài 4 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Tính các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{6x + 8}}{{5x - 2}}\);                     

b) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{6x + 8}}{{5x - 2}}\);                 

c) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}}\);

d) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}}\);            

e) \(\mathop {\lim }\limits_{x \to  - {2^ - }} \frac{{3{x^2} + 4}}{{2x + 4}}\);           

g) \(\mathop {\lim }\limits_{x \to  - {2^ + }} \frac{{3{x^2} + 4}}{{2x + 4}}\).

Phương pháp:

Sử dụng phương pháp:

- Chia cả tử và mẫu cho \({x^n}\), với n là số mũ cao nhất trong biểu thức đối với câu a, b.

- Câu c, d: \(\sqrt {{x^2}}  = \left| x \right| = \left\{ \begin{array}{l}x,x \to  + \infty \\ - x,x \to  - \infty \end{array} \right.\)

- Câu d, e sử dụng giới hạn cơ bản sau: \(\mathop {\lim }\limits_{x \to {a^ + }} \frac{1}{{x - a}} =  + \infty ;\mathop {\lim }\limits_{x \to {a^ - }} \frac{1}{{x - a}} =  - \infty \)

Lời giải:

Bài 5 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x + a}&{{\rm{  }}x < 2}\\4&{{\rm{  }}x = 2}\\{ - 3x + b}&{{\rm{ }}\,x > 2}\end{array}} \right.\)

a) Với \(a = 0,b = 1\), xét tính liên tục của hàm số tại \(x = 2\).

b) Với giá trị nào của a, b thì hàm số liên tục tại \(x = 2\) ?

c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?

Phương pháp:

- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = f\left( {{x_0}} \right)\)

- Các hàm đa thức liên tục trên \(\mathbb{R}\)

Lời giải:

Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{  }}x < 2}\\4&{{\rm{  }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) =  - 3.2 + 1 =  - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)

Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)

Vậy hàm số không liên tục tại x = 2.

b) Ta có:

 \(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) =  - 3.2 + b =  - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)

Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)

\( \Leftrightarrow  - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)

Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.

c) Tập xác định của hàm số là: ℝ.

Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.

Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.

Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.

Vậy với a = 0 và b = 10 thỏa mãn điều kiện.

Bài 6 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Từ độ cao \(55,8\;{\rm{m}}\) của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được trước đó. Gọi \({S_n}\) là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất \(n\) lần. Tính \(\lim {S_n}\).

Phương pháp:

Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).

Lời giải:

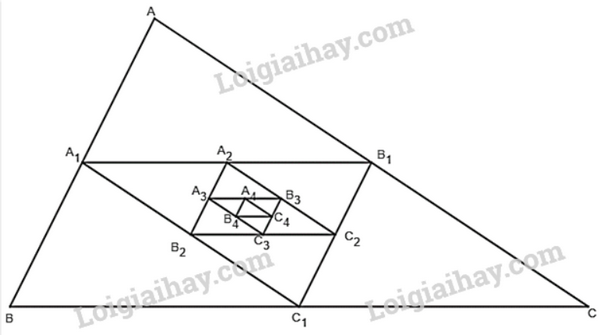
Bài 7 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).

a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).

b) Tìm các tổng \({p_1} + {p_2} +  \ldots  + {p_n} +  \ldots \) và \({S_1} + {S_2} +  \ldots  + {S_n} +  \ldots \).

Phương pháp:

Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).

Chu vi tam giác bằng tổng ba cạnh.

Diện tích tam giác bằng một nửa chiều cao nhân cạnh đáy tương ứng.

Lời giải:

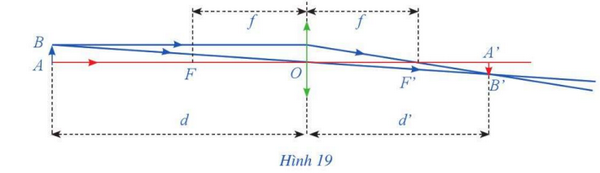
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)

Ta có:

 \({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)

\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)

\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)

+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)

Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).

Ta có:

\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)

\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).

b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:

\({p_1} + {p_2} +  \ldots  + {p_n} +  \ldots  = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)

+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:

\({S_1} + {S_2} +  \ldots  + {S_n} +  \ldots  = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)

Bài 8 trang 79 SGK Toán 11 tập 1 - Cánh Diều

Một thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\)  lần lượt là khoảng cách từ một vật thật AB và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính như Hình 19. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\).

a) Tìm biểu thức xác định hàm số \(d' = \varphi (d)\).     

b) Tìm \(\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d),\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\) và \(\mathop {\lim }\limits_{d \to f} \varphi (d)\). Giải thích ý nghĩa của các kết quả tìm được.

Phương pháp:

Sử dụng công thức \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\)

Lời giải:

Sachbaitap.com