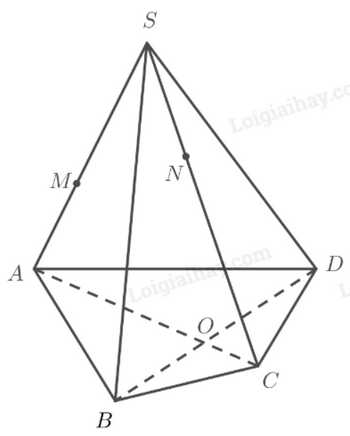
Giải SGK Toán 11 trang 99 Chân trời sáng tạo tập 1

Bài 1 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\).

a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\).

b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).

Lời giải:

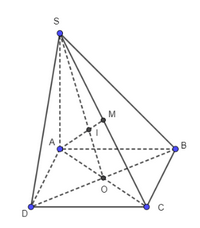
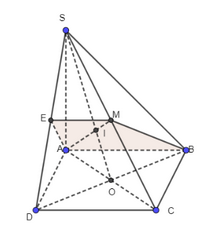
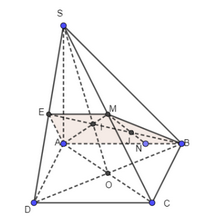
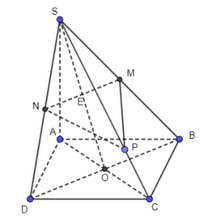
a) Ta có:

\(\left. \begin{array}{l}M \in SA \subset \left( {SAC} \right)\\N \in SC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow MN \subset \left( {SAC} \right)\)

b) Ta có:

\(\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)

Bài 2 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\) là trung điểm của \(SC\).

a) Tìm giao điểm \(I\) của đường thẳng \(AM\) và mặt phẳng \(\left( {SBD} \right)\). Chứng minh \(IA = 2IM\).

b) Tìm giao điểm \(E\) của đường thẳng \(S{\rm{D}}\) và mặt phẳng \(\left( {ABM} \right)\).

c) Gọi \(N\) là một điểm tuỳ ý trên cạnh \(AB\). Tìm giao điểm của đường thẳng \(MN\) và mặt phẳng \(\left( {SBD} \right)\).

Phương pháp:

‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.

‒ Để chứng minh \(IA = 2IM\), ta dựa vào tính chất trọng tâm của tam giác.

Lời giải:

a)

b)

Từ M kẻ đường thẳng song song với AB cắt SD tại E.

Ta có ME ⊂ (ABM).

Do đó SD ∩ (ABM) = {E}.

c)

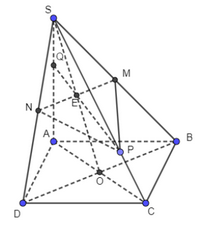
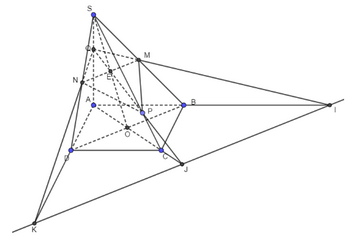
Gọi MN giao với BE tại J

Mà BE ⊂ (SBD)

Suy ra I là giao điểm của MN và (SBD).

Bài 3 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD\); \(M,N\) lần lượt là trung điểm của \(SB,SD\); \(P\) thuộc đoạn \(SC\) và không là trung điểm của \(SC\).

a) Tìm giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \(\left( {MNP} \right)\).

b) Tìm giao điểm \(Q\) của đường thẳng \(SA\) và mặt phẳng \(\left( {MNP} \right)\).

c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB\), \(QP\) và \(AC\), \(QN\) và \(A{\rm{D}}\). Chứng minh \(I,J,K\) thẳng hàng.

Phương pháp:

‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.

‒ Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.

Lời giải:

a) Gọi E là giao điểm của SO và MN

Mà MN ⊂ (MNP)

Suy ra SO ∩ (MNP) = {E}.

b)

Gọi Q là giao điểm của PE và SA

Mà PE ⊂ (MNP)

Suy ra SA ∩ (MNP) = {Q}.

c)

Ta có: QM ∩ AB = {I};

Mà QM ⊂ (QMN), AB ⊂ (ABCD)

Suy ra I ∈ (QMN) ∩ (ABC) (1)

Ta lại có: QN ∩ AD = {K}

Mà QN ⊂ (QMN), AD ⊂ (ABCD)

Suy ra K ∈ (QMN) ∩ (ABCD ) (2)

Từ (1) và (2) suy ra (QMN) ∩ (ABCD ) = {IM}.

Mặt khác, ta có: QE ∩ AC = {J}

Mà QE ⊂ (QMN), AC ⊂ (ABCD)

Suy ra J ∈ (QMN) ∩ (ABCD )

Do đó J thuộc đường thẳng IM.

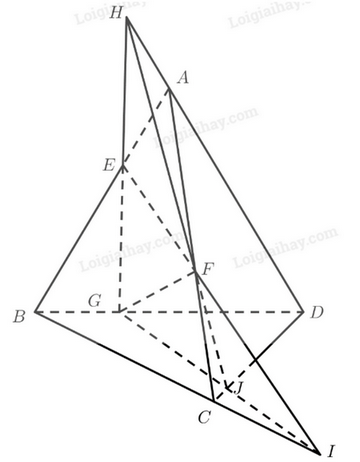
Bài 4 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho tứ diện \(ABCD\). Gọi \(E,F,G\) lần lượt là ba điểm trên ba cạnh \(AB,AC,BD\) sao cho \(EF\) cắt \(BC\) tại \(I\left( {I \ne C} \right)\), \(EG\) cắt \(A{\rm{D}}\) tại \(H\left( {H \ne D} \right)\).

a) Tìm giao tuyến của các mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\); \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\).

b) Chứng minh ba đường thẳng \(CD,IG,HF\) cùng đi qua một điểm.

Lời giải:

a) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}G \in \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow G \in \left( {EFG} \right) \cap \left( {BCD} \right)\\\left. \begin{array}{l}I \in EF \subset \left( {EFG} \right)\\I \in BC \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow I \in \left( {EFG} \right) \cap \left( {BCD} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\) là đường thẳng \(GI\).

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}F \in \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow F \in \left( {EFG} \right) \cap \left( {ACD} \right)\\\left. \begin{array}{l}H \in EG \subset \left( {EFG} \right)\\H \in A{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow H \in \left( {EFG} \right) \cap \left( {ACD} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\) là đường thẳng \(HF\).

b) Gọi \(J\) là giao điểm của \(CD\) và \(IG\).

Ta có:

\(\left. \begin{array}{l}J \in IG \subset \left( {EFG} \right)\\J \in C{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow J \in \left( {EFG} \right) \cap \left( {ACD} \right)\)

Mà \(F \in \left( {EFG} \right) \cap \left( {ACD} \right),H \in \left( {EFG} \right) \cap \left( {ACD} \right)\) (theo chứng minh phần a).

Do đó ba điểm \(H,F,J\) thẳng hàng.

Vậy ba đường thẳng \(CD,IG,HF\) cùng đi điểm \(J\).

Bài 5 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo

Thước laser phát ra tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình 41). Giải thích tại sao các thước kẻ laser lại giúp người thợ xây dựng kẻ được đường thẳng trên tường hoặc sàn nhà.

Phương pháp:

Áp dụng giao tuyến của hai mặt phẳng.

Lời giải:

Thước laser phát tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng, mặt phẳng ánh sáng này giao với mặt tường sẽ tạo ra một vệt là đường thẳng trên tường hoặc sàn nhà.

Sachbaitap.com