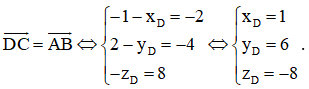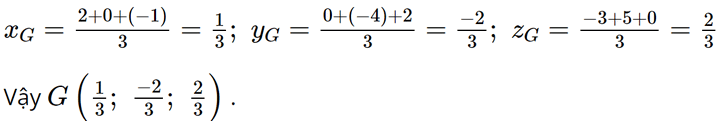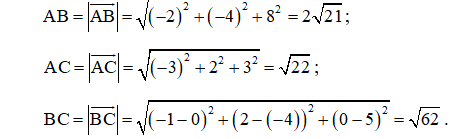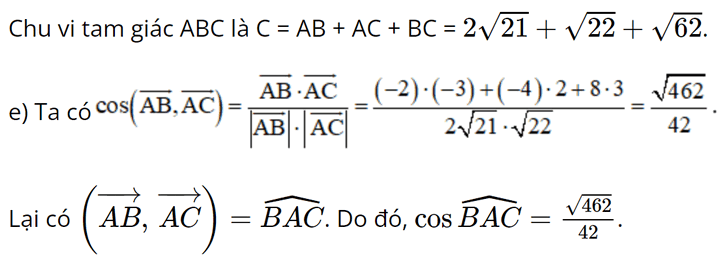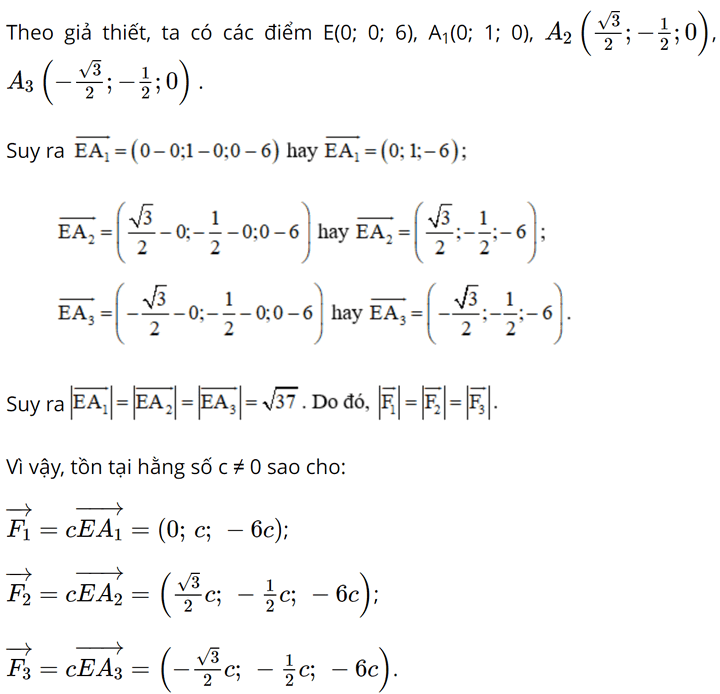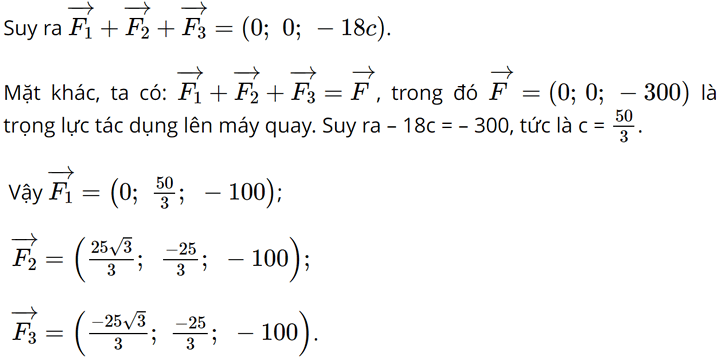Giải SGK Toán 12 tập 1 Cánh Diều trang 82, 83Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 82 bài 11, 12, 13, 14, 15 trang 83 SGK Toán 12 Cánh Diều tập 1. Trong không gian với hệ tọa độ Oxyz, cho A(2;0;-3), B(0;-4;5) và C(-1;2;0). a) Chứng minh rằng ba điểm A, B, C không thằng hàng b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành c) Tìm tọa độ trọng tâm G của tam giác ABC Bài 1 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho điểm M thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow i + 4\overrightarrow j + 2\overrightarrow k \). Tọa độ của điểm M là: A. (2;3;4) B. (3;4;2) C. (4,2,3) D. (3;2;4) Phương pháp: \(\overrightarrow {OM} = 3\overrightarrow i + 4\overrightarrow j + 2\overrightarrow k = (3;4;2) \Rightarrow M(3;4;2)\). Lời giải: Đáp án đúng là: B
Bài 2 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho hai điểm M(1;-2;3) và N(3;4;-5). Tọa độ của vecto \(\overrightarrow {NM} \) là: A. (-2;6;8) B. (2;6;-8) C. (-2;6;-8) D. (-2;-6;8) Phương pháp: Cho 2 điểm \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), ta có \(\overrightarrow {AB} = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})\) Lời giải: Đáp án đúng là: D
Bài 3 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho hai vecto \(\overrightarrow u = (3; - 4;5),\overrightarrow v = (5;7; - 1)\). Tọa độ của vecto \(\overrightarrow u + \overrightarrow v \) là: A. (8;3;4) B. (-2;-11;6) C. (2;11;-6) D. (-8;-3;-4) Phương pháp: Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\) Lời giải: Đáp án đúng là: A
Bài 4 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho hai vecto \(\overrightarrow u = (1; - 2;3),\overrightarrow v = (5;4; - 1)\). Tọa độ của vecto \(\overrightarrow u - \overrightarrow v \) là: A. (4;6;4) B. (-4;-6;4) C. (4;6;-4) D. (-4;-6;-4) Phương pháp: Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\) Lời giải: Đáp án đúng là: B
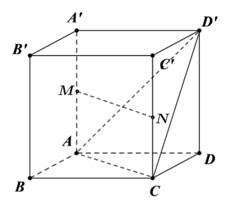
Bài 5 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho vecto \(\overrightarrow u = (1; - 1;3)\). Tọa độ của vecto \( - 3\overrightarrow u \) là: A. (3;-3;9)a B. (3;-3;-9) C. (-3;3;-9) D. (3;3;9) Phương pháp: Áp dụng quy tắc nhân vecto với một số. Lời giải: Đáp án đúng là: C Ta có Bài 6 trang 82 SGK Toán 12 Tập 1 Cánh Diều Độ dài của vecto \(\overrightarrow u = (2; - 2;1)\) là: A. 9 B. 3 C. 2 D. 4 Phương pháp: Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \) Lời giải: Đáp án đúng là: B Ta có Bài 7 trang 82 SGK Toán 12 Tập 1 Cánh Diều Tích vô hướng của hai vecto \(\overrightarrow u = (1; - 2;3),\overrightarrow v = (3;4; - 5)\) là: A. \(\sqrt {14} .\sqrt {50} \) B. \( - \sqrt {14} .\sqrt {50} \) C. 20 D. -20 Phương pháp: Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có biểu thức tọa độ của tích vô hướng \(\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\) Lời giải: Đáp án đúng là: D Ta có Bài 8 trang 82 SGK Toán 12 Tập 1 Cánh Diều Khoảng cách giữa hai điểm I(1;4;-7) và K(6;4;5) là: A. 169 B. 13 C. 26 D. 6,5 Phương pháp: Khoảng cách giữa hai điểm là độ lớn vecto nối hai điểm đó. Lời giải: Đáp án đúng là: B Ta có Bài 9 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho hai điểm M(1;-2;3) và N(3;4;-5). Trung điểm của đoạn thẳng MN có tọa độ là: A. (-2;1;1) B. (2;1;1) C. (-2;1;-1) D. (2;1;-1) Phương pháp: Cho 2 điểm \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB. Lời giải: Đáp án đúng là: D Gọi tọa độ trung điểm của đoạn thẳng MN là (x; y; z). Ta có Vậy tọa độ trung điểm của đoạn thẳng MN là (2; 1; – 1). Bài 10 trang 82 SGK Toán 12 Tập 1 Cánh Diều Cho tam giác MNP có M(0;2;1), N(-1;-2;3) và P(1;3;2). Trọng tâm của tam giác MNP có tọa độ là: A. (0;1;2) B. (0;3;6) C. (0;-3;-6) D. (0;-1;-2) Phương pháp: Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC. Lời giải: Đáp án đúng là: A Gọi tọa độ trọng tâm của tam giác MNP là (x; y; z). Ta có Vậy tọa độ trọng tâm của tam giác MNP là (0; 1; 2). Bài 11 trang 83 SGK Toán 12 Tập 1 Cánh Diều Cho hai vecto \(\overrightarrow u = (1; - 2;3),\overrightarrow v = (3;4; - 5)\). Hãy chỉ ra tọa độ của một vecto \(\overrightarrow w \) khác \(\overrightarrow 0 \) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) Phương pháp: Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) Lời giải: Ta có Bài 12 trang 83 SGK Toán 12 Tập 1 Cánh Diều Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA’ và CC’. Tính góc giữa hai vecto \(\overrightarrow {MN} \) và \(\overrightarrow {AD'} \) Phương pháp: \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\) Lời giải:
Vì M, N lần lượt là trung điểm của các cạnh AA' và CC' nên MN // AC, MN = AC.
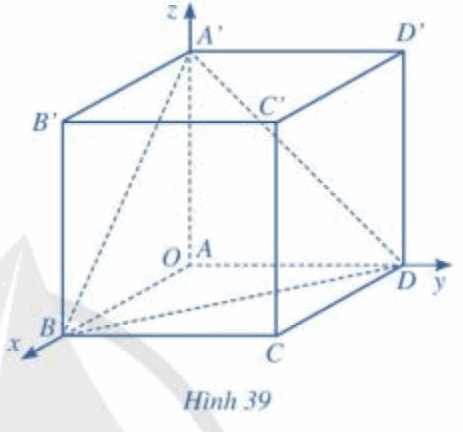
Bài 13 trang 83 SGK Toán 12 Tập 1 Cánh Diều Xét hệ tọa độ Oxyz gắn với hình lập phương ABCD.A’B’C’D’ như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1).
a) Xác định tọa độ các đỉnh còn lại của hình lập phương ABCD.A’B’C’D’ b) Xác định tọa độ trọng tâm G của tam giác A’BD c) Xác định tọa độ các vecto \(\overrightarrow {OG} \) và \(\overrightarrow {OC'} \). Chứng minh rằng ba điểm O, G, C’ thẳng hàng và \(OG = \frac{1}{3}OC\) Phương pháp: a) Quan sát hình vẽ b) Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC c) A, B, C thẳng hàng khi \(\overrightarrow {AB} = k\overrightarrow {AC} \) Lời giải: a) Ta có điểm C thuộc mặt phẳng (Oxy) nên cao độ của điểm C bằng 0. Lại có CB ⊥ Ox tại B nên hoành độ của điểm C là 1, CD ⊥ Oy tại D nên tung độ của điểm C là 1. Vậy C(1; 1; 0).
Tương tự như vậy, ta xác định được B'(1; 0; 1) và D'(0; 1; 1).
Suy ra hai vectơ
Bài 14 trang 83 SGK Toán 12 Tập 1 Cánh Diều Trong không gian với hệ tọa độ Oxyz, cho A(2;0;-3), B(0;-4;5) và C(-1;2;0). a) Chứng minh rằng ba điểm A, B, C không thằng hàng b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành c) Tìm tọa độ trọng tâm G của tam giác ABC d) Tính chu vi của tam giác ABC e) Tính \(\cos \overrightarrow {BAC} \) Phương pháp: a) A, B, C không thẳng hàng khi \(\overrightarrow {AB} \ne k\overrightarrow {AC} \) b) Tứ giác ABCD là hình bình hành khi có một cặp cạnh đối song song và bằng nhau c) Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC d) Chu vi tam giác bằng tổng độ dài 3 cạnh e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\) Lời giải:
Vậy ba điểm A, B, C không thẳng hàng. b) Gọi tọa độ điểm D là (xD; yD; zD). Ta có Tứ giác ABCD là hình bình hành khi
Vậy D(1; 6; – 8). c) Gọi tọa độ trọng tâm G của tam giác ABC là (xG; yG; zG). Ta có
d) Ta có
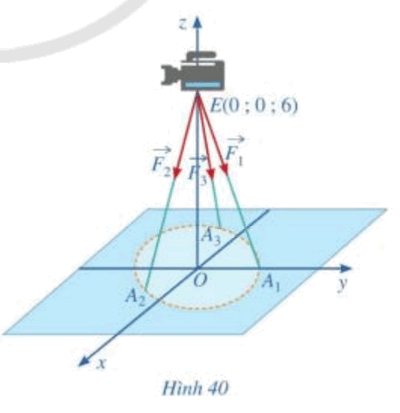
Bài 15 trang 83 SGK Toán 12 Tập 1 Cánh Diều Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \({A_1}(0;1;0)\), \({A_2}(\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\), \({A_3}( - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\) (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)
Phương pháp: Vì đèn cân bằng nên trọng lực của đèn sẽ phân bố đều trên các chân của giá đỡ. Từ tọa độ các điểm đã cho, ta tìm được cái mối liên hệ với vecto lực và tìm được tọa độ của các vecto lực. Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 2
|

 Tải ngay
Tải ngay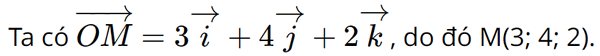
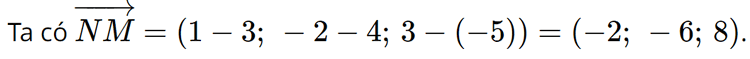
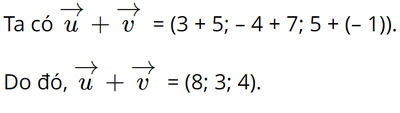
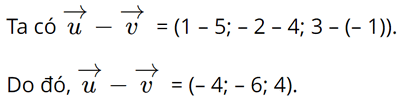
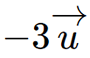
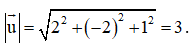
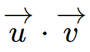
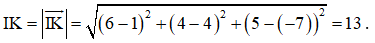
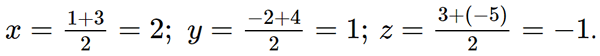
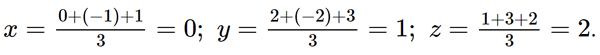
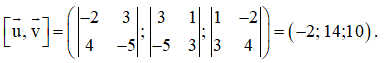

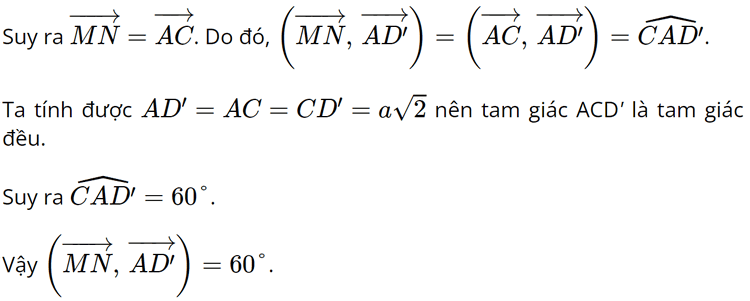
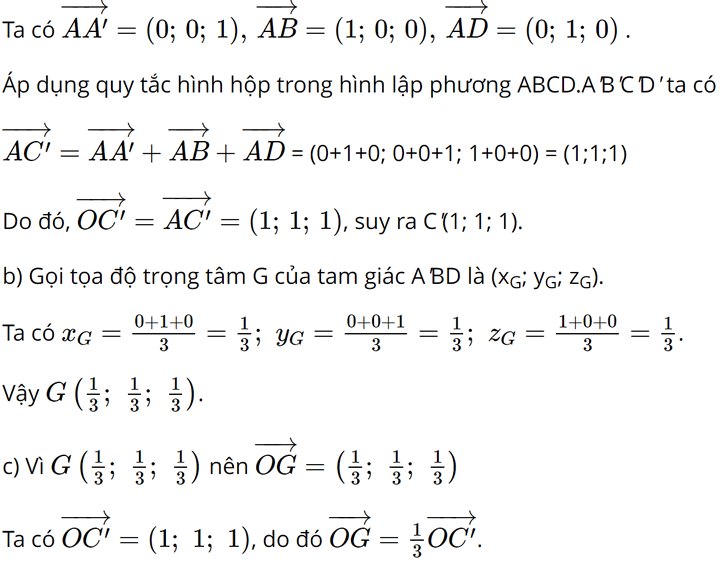
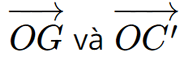
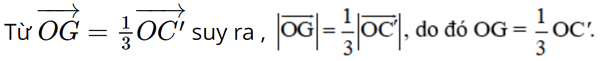
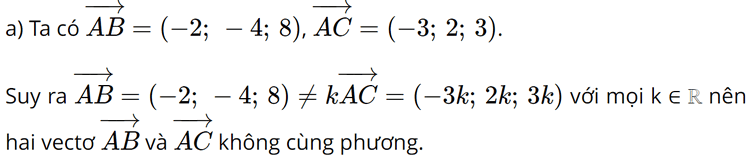
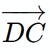 = (– 1 – xD; 2 – yD; – zD).
= (– 1 – xD; 2 – yD; – zD).