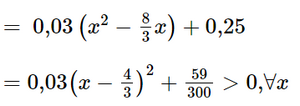Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 13Giải bài 1, 2, 3, 4, 5, 6, 7 trang 13 SGK Toán 12 Chân trời sáng tạo tập 1. Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức với x là số năm tính từ 2010 đến 2017. Bài 1 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
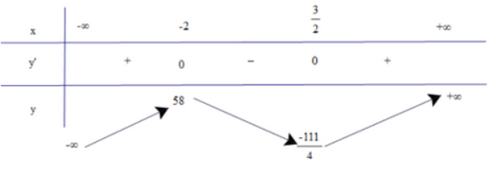
Phương pháp: Quan sát đồ thị Lời giải: a) Dựa vào đồ thị ta có: Hàm số nghịch biến trên các khoảng (−1; 0) và (2; 4). Hàm số đồng biến trên các khoảng (0; 2) và (4; 5). Hàm số đạt cực tiểu tại x = 0; x = 4 và yCT = −1. Hàm số đạt cực đại tại x = 2 và yCĐ = 2. b) Dựa vào đồ thị ta có: Hàm số đồng biến trên các khoảng (−3; −1) và (1; 3). Hàm số nghịch biến trên khoảng (−1;1). Hàm số đạt cực đại tại x = −1 và yCĐ = 3. Hàm số đạt cực tiểu tại x = 1 và yCT = −1. Bài 2 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: a) \(y = 4{x^3} + 3{x^2}--36x + 6\) b) \(y = \frac{{{x^2} - 2x - 7}}{{x - 4}}\) Phương pháp: Tìm tập xác định, đạo hàm và lập bảng biến thiên Lời giải: a) Tập xác định: D = ℝ. Ta có y' = 12x2 + 6x – 36; y' = 0 ⇔ 12x2 + 6x – 36 = 0 ⇔ x = −2 hoặc Bảng biến thiên
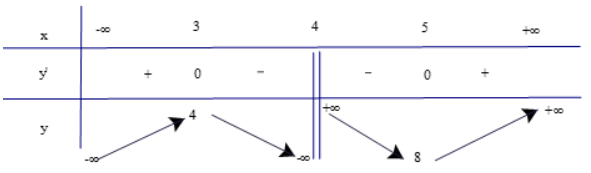
Dựa vào bảng biến thiên, ta có: Hàm số đồng biến trên các khoảng Hàm số nghịch biến trên khoảng Hàm số đạt cực đại tại x = −2 và yCĐ = 58. Hàm số đạt cực tiểu tại b) Tập xác định: D = ℝ\{4}.
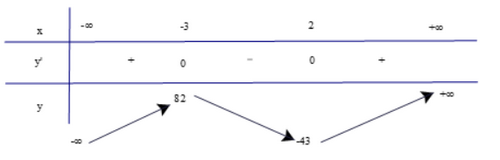
Có y' = 0 ⇔ x2 – 8x + 15 = 0 ⇔ x = 3 hoặc x = 5. Bảng biến thiên Dựa vào bảng biến thiên ta có: Hàm số đồng biến trên các khoảng (−∞; 3) và (5; +∞). Hàm số nghịch biến trên các khoảng (3; 4) và (4; 5). Hàm số đạt cực đại tại x = 3 và yCĐ = 4. Hàm số đạt cực tiểu tại x = 5 và yCT = 8. Bài 3 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Tìm cực trị của các hàm số sau: a) \(y = 2{x^3} + 3{x^2}--36x + 1\) b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\) c) \(y = \sqrt { - {x^2} + 4} \) Phương pháp: Tìm tập xác định, đạo hàm và lập bảng biến thiên Lời giải: a) Tập xác định: D = ℝ. Có y' = 6x2 + 6x – 36; y' = 0 ⇔ 6x2 + 6x – 36 = 0 ⇔ x = −3 hoặc x = 2. Bảng biến thiên
Dựa vào bảng biến thiên, ta có: Hàm số đạt cực đại tại x = −3 và yCĐ = 82. Hàm số đạt cực tiểu tại x = 2 và yCT = −43. b) Tập xác định: D = ℝ\{2}.
Bảng biến thiên
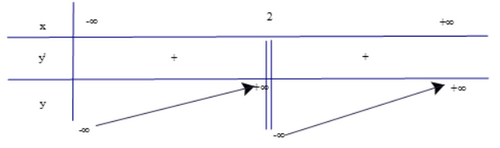
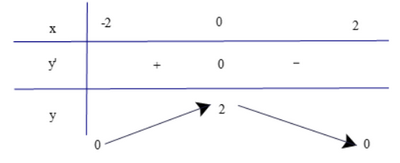
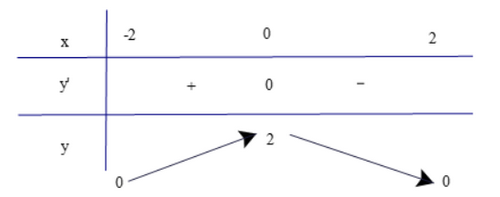
Hàm số không có cực trị. c) Tập xác định: D = [−2; 2].
Bảng biến thiên
Dựa vào bảng biến thiên ta có: Hàm số đạt cực đại tại x = 0 và yCĐ = 2. Hàm số không có cực tiểu. Bài 4 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Chứng minh rằng hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) nghịch biến trên từng khoảng xác định của nó Phương pháp: Tìm tập xác định, đạo hàm và xét dấu đạo hàm Lời giải: Tập xác định: D = ℝ\{3}.
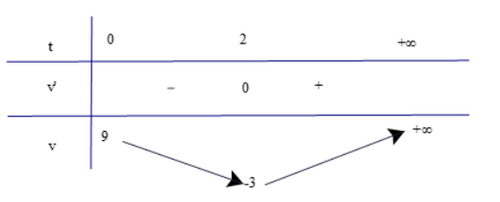
Do đó hàm số nghịch biến trên (−∞; 3) và (3; +∞). Vậy hàm số Bài 5 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức \(f\left( x \right) = 0,01{x^3}--0,04{x^2} + 0,25x + 0,44\) (tỉ USD) với x là số năm tính từ 2010 đến 2017 (\(0 \le x \le 7\)). Phương pháp: Áp dụng công thức tính đạo hàm, xét dấu đạo hàm Lời giải: a) f'(x) = 0,03x2 – 0,08x + 0,25. b) Có f'(x) = 0,03x2 – 0,08x + 0,25 Do đó f(x) là hàm đồng biến. Điều này chứng tỏ kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017. Bài 6 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\).Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t)\); \(v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\). a) Tìm các hàm \(v(t)\)và \(a(t)\) b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm? Phương pháp: Áp dụng công thức tính đạo hàm, xét dấu đạo hàm Lời giải: a) Ta có v(t) = x'(t) = 3t2 −12t + 9; a(t) = v'(t) = 6t – 12. b) Để tìm khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm ta đi xét sự biến thiên của hàm v(t). Có v'(t) = 0 ⇔ 6t – 12 = 0 ⇔ t = 2. Bảng biến thiên
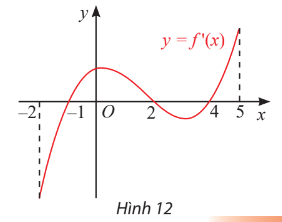
Dựa vào bảng biến thiên ta có: Vận tốc của chất điểm tăng khi t > 2 và vận tốc của chất điểm giảm khi 0 < t < 2. Bài 7 trang 13 SGK Toán 12 Tập 1 Chân trời sáng tạo Đạo hàm f '(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).
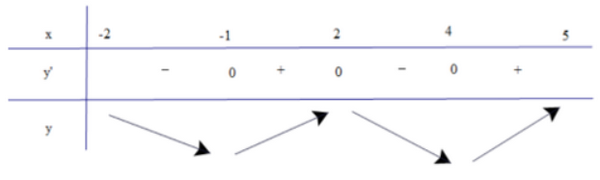
Phương pháp: Quan sát đồ thị, xét dấu của f’(x) Lời giải: Dựa vào đồ thị của hàm y = f'(x), ta có bảng biến thiên
Dựa vào bảng biến thiên ta có: Hàm số y = f(x) đồng biến trên các khoảng (−1; 2) và (4; 5). Hàm số y = f(x) nghịch biến trên các khoảng (−2; −1) và (2; 4). Hàm số y = f(x) đạt cực tiểu tại x = −1 và x = 4. Hàm số y = f(x) đạt cực đại tại x = 2. Sachbaitap.com
Xem thêm tại đây:
Bài 1: Tính đơn diệu và cực trị của hàm số
|
-

Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 18
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 18 SGK Toán 12 Chân trời sáng tạo tập 1. Hộp sữa (1l) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

 Tải ngay
Tải ngay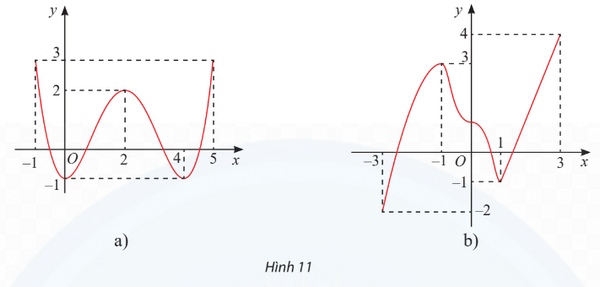
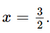
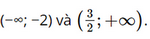
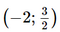
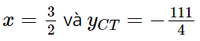
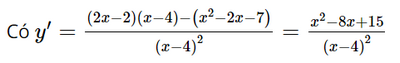
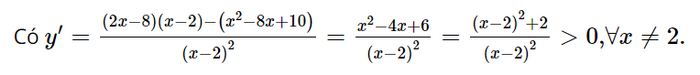
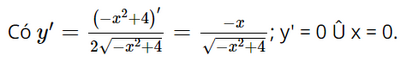
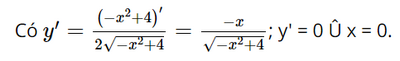
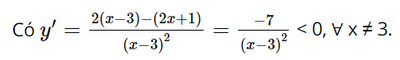
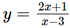 nghịch biến trên từng khoảng xác định của nó.
nghịch biến trên từng khoảng xác định của nó.