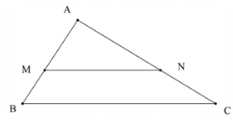
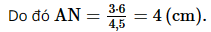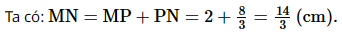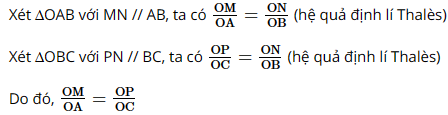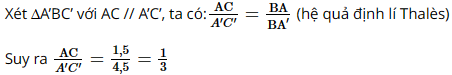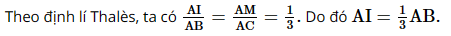Giải SGK Toán 8 Cánh Diều tập 2 trang 57Giải bài 1, 2, 3, 4, 5 trang 57 SGK Toán lớp 8 Cánh Diều tập 2. Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không cần dùng thước đo. Bài 1 trang 57 SGK Toán 8 - Cánh Diều tập 2 Cho tam giác ABC có \(AB = 4,5cm,\,\,AC = 6cm\). Các điểm M, N lần lượt thuộc các cạnh AB, AC thỏa mãn \(AM = 3cm\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng AN. Phương pháp: Dựa vào hệ quả của định lý Thales để tính độ dài đoạn thẳng AN. Lời giải:
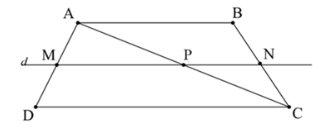
Xét ∆ABC với MN // BC, ta có:
Bài 2 trang 57 SGK Toán 8 - Cánh Diều tập 2 Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P. a) Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\); b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA. Phương pháp: Dựa vào hệ quả của định lý Thales để tính độ dài đoạn thẳng AN. Lời giải:
a) Do d // CD, mà M, N, P ∈ d nên MP // CD, PN // CD, MN // CD Do ABCD là hình thang nên AB // CD, do đó PN // AB
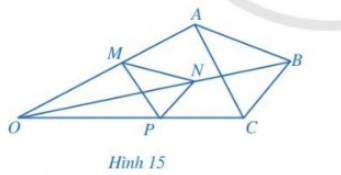
Bài 3 trang 57 SGK Toán 8 - Cánh Diều tập 2 Trong Hình 15, cho \(MN\parallel AB,\,\,NP\parallel BC\). Chứng minh \(MP\parallel AC\).
Phương pháp: Dựa vào định lý Thales đảo để chứng minh \(MP\parallel AC\). Lời giải:
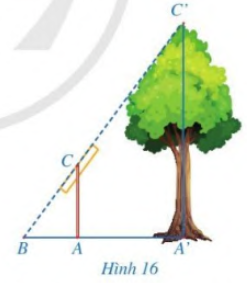
Bài 4 trang 57 SGK Toán 8 - Cánh Diều tập 2 Trong Hình 16, độ dài đoạn thẳng A’C’ mô tả chiều cao của một cái cây, đoạn thẳng AC mô tả một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm A’, A, B). Giả sử \(AC = 2m,\,\,AB = 1,5m,\,\,A'B = 4,5m\). Tính chiều cao của cây.
Phương pháp: - Chứng minh \(AC\parallel A'C'\). - Dựa vào hệ quả của định lý Thales để tính độ dài A’C’. Lời giải: Ta có: AC ⊥ A’B, A’C’ ⊥ A’B nên AC // A’C’
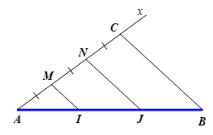
Suy ra A’C’ = 3AC = 3.2 = 6 (m). Vậy cây cao 6m. Bài 5 trang 57 SGK Toán 8 - Cánh Diều tập 2 Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không cần dùng thước đo. Phương pháp: Lấy thêm điểm và sử dụng định lý Thales để chia đoạn thẳng thành ba phần bằng nhau. Lời giải:
– Vẽ tia Ax và lấy một điểm M trên tia Ax. – Dùng compa vẽ cung tròn tâm M, bán kính MA, cắt tia Ax tại N (khác A), ta được MN = MA. Tương tự như vậy, khi đó ta lấy liên tiếp trên tia Ax, bắt đầu từ điểm A, ba đoạn thẳng AM, MN, NC có độ dài bằng nhau. – Trong tam giác ABC, kẻ đường thẳng qua M song song với cạnh BC, cắt cạnh AB tại I.
Dựa theo đoạn mẫu AI, ta có thể chia đoạn thẳng AB thành ba phần bằng nhau. Sachbaitap.com
Xem thêm tại đây:
Bài 1. Định lí Thalès trong tam giác
|
-

Giải SGK Toán 8 Cánh Diều tập 2 trang 60, 61
Giải bài 1 trang 60, bài 2, 3, 4 trang 61 SGK Toán lớp 8 Cánh Diều tập 2. Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được (AC = 50m,CD = 20m,DE = 18m). Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?

 Tải ngay
Tải ngay