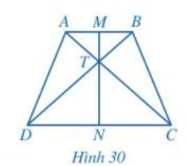
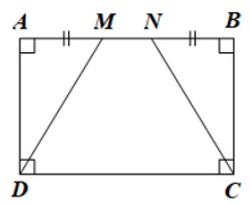
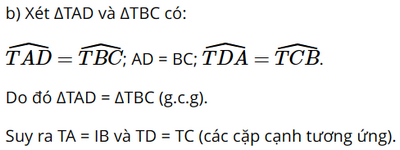Giải SGK Toán 8 trang 103, 104 Cánh Diều tập 1

Bài 1 trang 103 SGK Toán 8 tập 1 - Cánh Diều

Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần luợt là trung điểm của cạnh AB, CD và T là giao điểm của AC và BD (hình 30)

a) \(\widehat {TA{\rm{D}}} = \widehat {TBC},\widehat {T{\rm{D}}A} = \widehat {TCB}\)

b) \(TA = TB,T{\rm{D}} = TC\)

c) MN là đường trung trực của cả hai đoạn thẳng AB và CD

Phương pháp:

Vận dụng các tính chất của hình thang cân để chứng minh.

+ Hai cạnh bên bằng nhau

+ Hai đường chéo bằng nhau

Lời giải:

a) Do ABCD là hình thang cân nên AC = BD và AD = BC (tính chất hình thang cân).

Xét ΔADC và ΔBCD có:

AD = BC; AC = BD; DC là cạnh chung

Do đó ΔADC = ΔBCD (c.c.c)

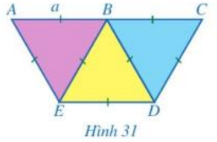
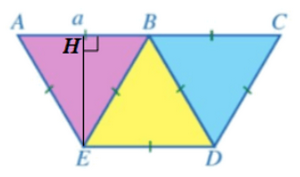
c) • Do TA = TB nên tam giác TAB cân tại T.

ΔTAB cân tại T có TM vừa là đường trung tuyến vừa là đường cao do đó TM là đường trung trực của đoạn thẳng AB nên TM ⊥ AB.

• Do TD = TC nên tam giác TCD cân tại T.

ΔTCD cân tại T có TN vừa là đường trung tuyến vừa là đường cao do đó TN là đường trung trực của đoạn thẳng CD nên TN ⊥ CD.

• Do AB // CD, TM ⊥ AB, TN ⊥ CD nên T, M, N thẳng hàng

Hay MN là đường trung trực của cả hai đoạn thẳng AB và CD.

Bài 2 trang 104 SGK Toán 8 tập 1 - Cánh Diều

Người ta ghép ba hình tam giác đều với độ dài cạnh là a với vị trí như Hình 31.

a) Chứng minh ba điểm A, B, C thẳng hàng

b) Chứng minh tứ giác ACDE là hình thang cân.

c) Tính diện tích của tứ giác ACDE theo a.

Phương pháp:

Quan sát hình 3.

Lời giải:

c) Vẽ đường cao EH của tam giác AEB.

Bài 3 trang 104 SGK Toán 8 tập 1 - Cánh Diều

Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho \(AM = NB < \dfrac{1}{2}AB\). Chứng minh tứ giác MNCD là hình thang cân

Phương pháp:

Chứng minh MNCD là hình thang có 2 đường chéo bằng nhau

Lời giải:

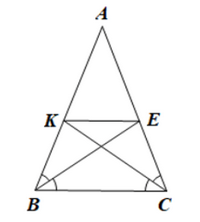
Bài 4 trang 104 SGK Toán 8 tập 1 - Cánh Diều

Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.

Phương pháp:

Chứng minh BKEC là hình thang có \(\widehat {ABC} = \widehat {ACB}\)

Lời giải:

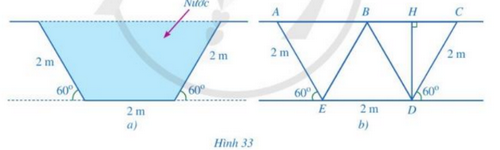
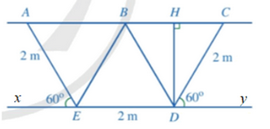
Bài 5 trang 104 SGK Toán 8 tập 1 - Cánh Diều

Hình 33 là mặt cắt đứng phần chứa nước của một con mương (hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC. H là hình chiếu của D trên đường thẳng BC.

a) Chứng minh rằng các tam giác BCD, BDE, ABE là các tam giác đều

b) Tính độ dài của DH, AC

c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước.

Phương pháp:

Vận dụng tính chất của hình thang cân

+ Hai cạnh bên bằng nhau

+ Hai đường chéo bằng nhau

Lời giải:

Sachbaitap.com