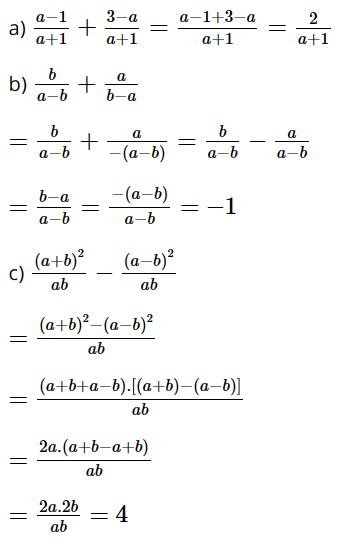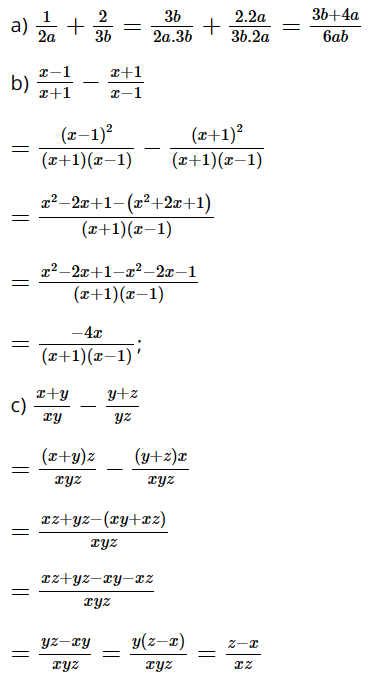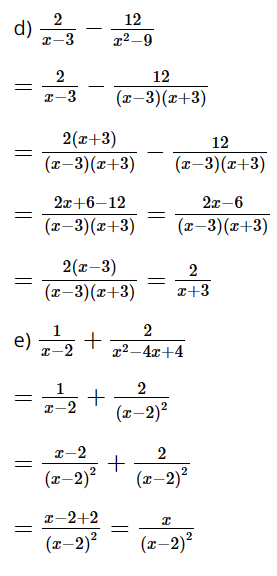Giải SGK Toán 8 trang 35 Chân trời sáng tạo tập 1

Bài 1 trang 35 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép cộng, trừ phân thức sau:

a) \(\dfrac{{a - 1}}{{a + 1}} + \dfrac{{3 - a}}{{a + 1}}\)                  b) \(\dfrac{b}{{a - b}} + \dfrac{a}{{b - a}}\)                 c) \(\dfrac{{{{\left( {a + b} \right)}^2}}}{{ab}} - \dfrac{{{{\left( {a - b} \right)}^2}}}{{ab}}\)

Phương pháp:

Đưa các phân thức về cùng mẫu rồi thực hiện phép cộng, trừ với các phân thức cùng mẫu đó.

Lời giải:

Bài 2 trang 35 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép cộng, trừ phân thức sau:

a) \(\dfrac{1}{{2a}} + \dfrac{2}{{3b}}\)

b) \(\dfrac{{x - 1}}{{x + 1}} - \dfrac{{x + 1}}{{x - 1}}\)

c) \(\dfrac{{x + y}}{{xy}} - \dfrac{{y + z}}{{yz}}\)

d) \(\dfrac{2}{{x - 3}} - \dfrac{{12}}{{{x^2} - 9}}\)

e) \(\dfrac{1}{{x - 2}} + \dfrac{2}{{{x^2} - 4x + 4}}\)

Phương pháp:

Đưa các phân thức về cùng mẫu rồi thực hiện cộng, trừ với các phân thức cùng mẫu đó.

Lời giải:

Bài 3 trang 35 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép tính sau:

a) \(\dfrac{{x + 2}}{{x - 1}} - \dfrac{{x - 3}}{{x - 1}} - \dfrac{{x - 4}}{{1 - x}}\)

b) \(\dfrac{1}{{x + 5}} - \dfrac{1}{{x - 5}} + \dfrac{{2x}}{{{x^2} - 25}}\)

c) \(x + \dfrac{{2{y^2}}}{{x + y}} - y\)

Phương pháp:

Đưa các phân thức về cùng mẫu rồi thực hiện phép tính với các phân thức cùng mẫu đó.

Lời giải:

a) ĐKXĐ: \(x \ne 1\)

\(\dfrac{{x + 2}}{{x - 1}} - \dfrac{{x - 3}}{{x - 1}} - \dfrac{{x - 4}}{{1 - x}}\) \( = \dfrac{{x + 2}}{{x - 1}} - \dfrac{{x - 3}}{{x - 1}} + \dfrac{{x - 4}}{{x - 1}} = \dfrac{{x + 2 - x + 3 + x - 4}}{{x - 1}} = \dfrac{{x + 1}}{{x - 1}}\)

b) ĐKXĐ: \(x \ne  \pm 5\)

\(\dfrac{1}{{x + 5}} - \dfrac{1}{{x - 5}} + \dfrac{{2x}}{{{x^2} - 25}}\) \( = \dfrac{{\left( {x - 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} - \dfrac{{\left( {x + 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} + \dfrac{{2x}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} = \dfrac{{x - 5 - x - 5 + 2x}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} = \dfrac{{2x - 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\)

\( = \dfrac{{2\left( {x - 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} = \dfrac{2}{{x + 5}}\)  

c) ĐKXĐ: \(x \ne  - y\)

\(x + \dfrac{{2{y^2}}}{{x + y}} - y\) \( = \dfrac{{x\left( {x + y} \right)}}{{x + y}} + \dfrac{{2{y^2}}}{{x + y}} - \dfrac{{y\left( {x + y} \right)}}{{x + y}} = \dfrac{{{x^2} + xy + 2{y^2} - xy - {y^2}}}{{x + y}} = \dfrac{{{x^2} + {y^2}}}{{x + y}}\)  

Bài 4 trang 35 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cùng đi từ thành phố A đến thành phố B cách nhau \(450\)km, xe khách chạy với tốc độ \(x\) (km/h); xe tải chạy với tốc độ \(y\) (km/h) (\(x > y\)). Nếu xuất phát cùng lúc thì xe khách đến thành phố B sớm hơn xe tải bao nhiêu giờ?

Phương pháp:

Vận dụng công thức tính thời gian theo quãng đường và vận tốc.

Lời giải:

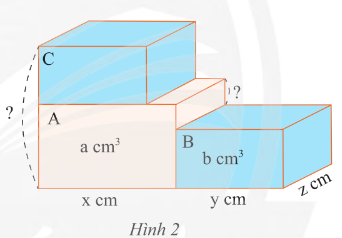
Bài 5 trang 35 SGK Toán 8 tập 1 - Chân trời sáng tạo

Có ba hình hộp chữ nhật A, B, C có chiều dài, chiều rộng và thể tích được cho như hình 2. Hình B và C có các kích thước giống nhau, hình A có cùng chiều rộng với B và C.

a) Tính chiều cao của các hình hộp chữ nhật. Biểu thị chúng bằng các phân thức cùng mẫu số.

b) Tính tổng chiều cao của hình A và C, chênh lệch chiều cao của hình A và B.

Phương pháp:

a. Sử dụng công thức tính thể tích hình hộp chữ nhật để viết công thức tính chiều dài, chiều rộng, chiều cao tương ứng.

b. Đưa các phân thức về cùng mẫu để thực hiện phép tính với các phân thức cùng mẫu đó.

Lời giải:

Sachbaitap.com