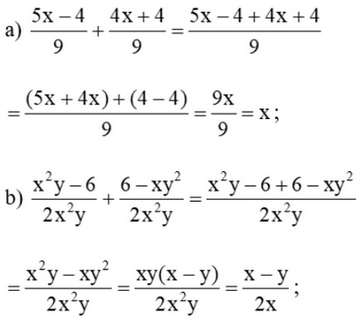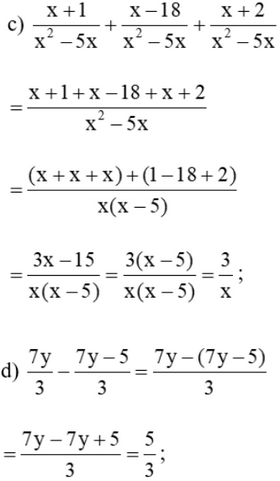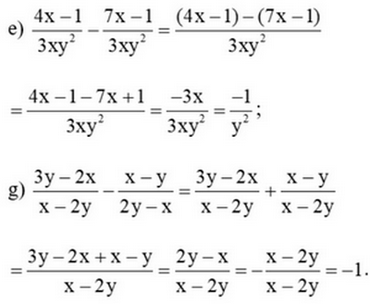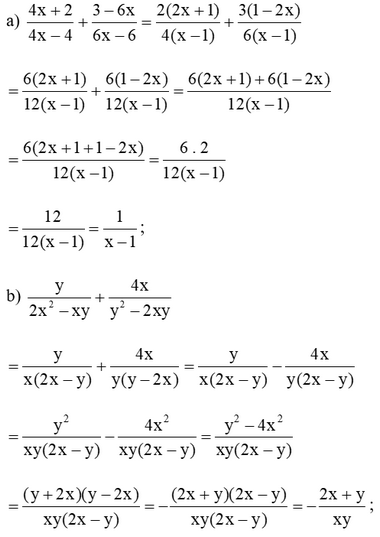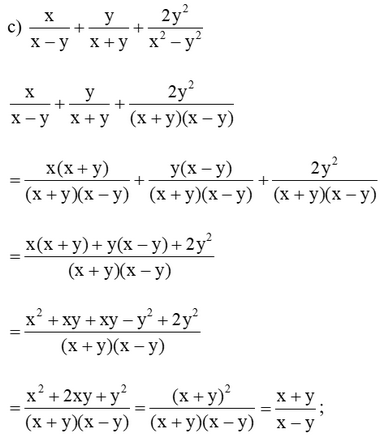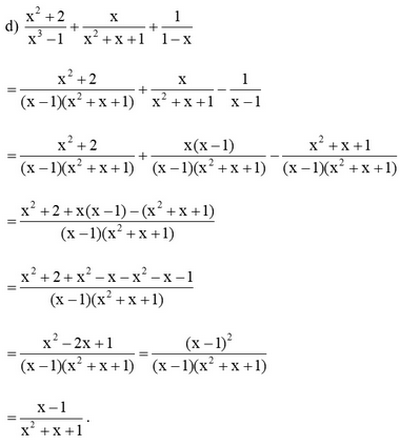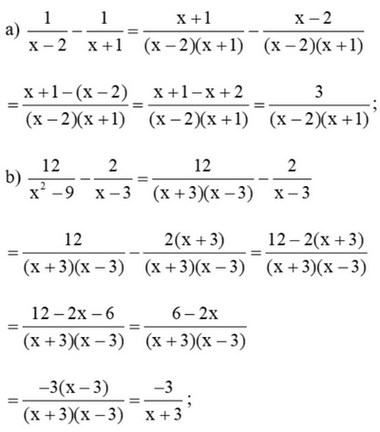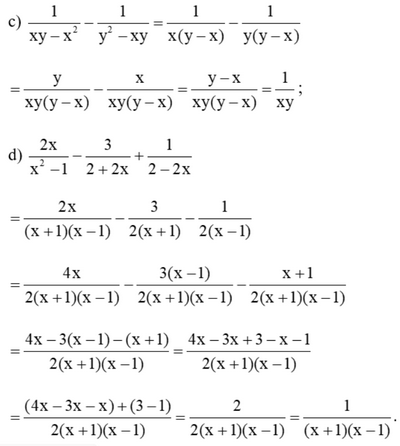Giải SGK Toán 8 trang 42, 43 Cánh Diều tập 1

Bài 1 trang 42 SGK Toán 8 tập 1 - Cánh Diều

Thực hiện phép tính:

\(a)\dfrac{{5{\rm{x}} - 4}}{9} + \dfrac{{4{\rm{x}} + 4}}{9}\)                                            

b) \(\dfrac{{{x^2}y - 6}}{{2{{\rm{x}}^2}y}} + \dfrac{{6 - x{y^2}}}{{2{{\rm{x}}^2}y}}\)

c) \(\dfrac{{x + 1}}{{{x^2} - 5{\rm{x}}}} + \dfrac{{x - 16}}{{{x^2} - 5{\rm{x}}}} + \dfrac{{x + 2}}{{{x^2} - 5{\rm{x}}}}\)                           \(d)\dfrac{{7y}}{3} - \dfrac{{7y - 5}}{3}\)

e) \(\dfrac{{4{\rm{x}} - 1}}{{3{\rm{x}}{y^2}}} - \dfrac{{7{\rm{x}} - 1}}{{3{\rm{x}}{y^2}}}\)                                                 \(g)\dfrac{{3y - 2{\rm{x}}}}{{x - 2y}} - \dfrac{{x - y}}{{2y - x}}\)

Phương pháp:

Áp dụng quy tắc cộng, trừ hai phân thức cùng mẫu, khác mẫu và phân thức đối để thực hiện các phép tính.

Lời giải:

Bài 2 trang 42 SGK Toán 8 tập 1 - Cánh Diều

Thực hiện phép tính:

\(a)\dfrac{{4{\rm{x}} + 2}}{{4{\rm{x  -  4}}}} + \dfrac{{3 - 6{\rm{x}}}}{{6{\rm{x}} - 6}}\)                                   \(b)\dfrac{y}{{2{{\rm{x}}^2} - xy}} + \dfrac{{4{\rm{x}}}}{{{y^2} - 2{\rm{x}}y}}\)

\(c)\dfrac{x}{{x - y}} + \dfrac{y}{{x + y}} + \dfrac{{2{y^2}}}{{{x^2} - {y^2}}}\)                       \(d)\dfrac{{{x^2} + 2}}{{{x^3} - 1}} + \dfrac{x}{{{x^2} + x + 1}} + \dfrac{1}{{1 - x}}\)

Phương pháp:

Áp dụng quy tắc cộng, trừ hai phân thức cùng mẫu, khác mẫu và phân thức đối để thực hiện các phép tính.

Lời giải:

Bài 3 trang 42 SGK Toán 8 tập 1 - Cánh Diều

Thực hiện phép tính:

a) \(\frac{1}{{x - 2}} - \frac{1}{{x + 1}}\)                                

b) \(\frac{{12}}{{{x^2} - 9}} - \frac{2}{{x - 3}}\)

c) \(\frac{1}{{xy - {x^2}}} - \frac{1}{{{y^2} - xy}}\)                      

d) \(\frac{{2{\rm{x}}}}{{{x^2} - 1}} - \frac{3}{{2 + 2{\rm{x}}}} + \frac{1}{{2 - 2{\rm{x}}}}\)

Phương pháp:

Áp dụng quy tắc cộng, trừ hai phân thức cùng mẫu, khác mẫu và phân thức đối để thực hiện các phép tính.

Lời giải:

Bài 4 trang 43 SGK Toán 8 tập 1 - Cánh Diều

a) Rút gọn biểu thức: \(A = \dfrac{{2{{\rm{x}}^2} + 1}}{{{x^3} + 1}} + \dfrac{{1 - x}}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}}\)

b) tính giá trị của A tại x = -3

Phương pháp:

a) Quy đồng mẫu thức chung để rút gọn biểu thức A

b) Thay x = -3 vào biểu thức A đã rút gọn để tính giá trị

Lời giải:

a) \(\begin{array}{l}A = \dfrac{{2{{\rm{x}}^2} + 1}}{{{x^3} + 1}} + \dfrac{{1 - x}}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}}\\A = \dfrac{{2{{\rm{x}}^2} + 1}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} + \dfrac{{\left( {1 - x} \right)\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} - \dfrac{{{x^2} - x + 1}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}}\\ = \dfrac{{2{{\rm{x}}^2} + 1 + 1 - {x^2} - {x^2} + x - 1}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \dfrac{{1 + x}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \dfrac{1}{{{x^2} - x + 1}}\end{array}\)

b) Với x = -3 ta thay vào biểu thức A đã rút gọn ta được:

\(A = \dfrac{1}{{{{\left( { - 3} \right)}^2} - \left( { - 3} \right) + 1}} = \dfrac{1}{{9 + 3 + 1}} = \dfrac{1}{{13}}\)

Bài 5 trang 43 SGK Toán 8 tập 1 - Cánh Diều

Một xí nghiệp dự định sản xuất 10 000 sản phẩm trong x ngày. Khi thực hiện, xí nghiệp đã làm xong sớm hơn 1 ngày so với dự định và còn làm thêm được 80 sản phẩm. Viết phân thức biểu thị theo x.

a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định.

b) Số sản phẩm xí nghiệp làm trong 1 ngày theo thực tế.

c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong một ngày theo dự định.

Phương pháp:

Số sản phẩm trong ngày bằng tổng số sản phẩm đã sản xuất chia cho số ngày.

Lời giải:

Bài 6 trang 43 SGK Toán 8 tập 1 - Cánh Diều

Người ta mở hai vòi nước cùng chảy vào một bể không chứa nước. Thời gian để vòi thứ nhất chảy một mình đẩy bể ít hơn thời gian vòi thức hai chảy một mình đầy bể là 2 giờ. Gọi x (giờ) là thời gian vòi thứ nhất chảy một mình đầy bể. Viết phân thức biểu thị theo x:

a) Thời gian vòi thứ hai chảy một mình đầy bể.

b) Phần bể mà mỗi vòi chảy được trong 1 giờ.

c) Phần bể mà cả hai vòi chảy được trong 1 giờ.

Phương pháp:

Phần bể mỗi vòi chảy trong một giờ là: 1 : (Tổng số thời gian chảy đầy bể)

Lời giải:

a) Theo đề bài, thời gian để vòi thứ nhất chảy một mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ.

Hay thời gian để vòi thứ hai chảy một mình đầy bể nhiều hơn thời gian để vòi thứ nhất chảy một mình đầy bể là 2 giờ.

Do đó, thời gian vòi thứ hai chảy một mình đầy bể là: x + 2 (giờ).

Bài 7 trang 43 SGK Toán 8 tập 1 - Cánh Diều

Để hưởng ứng phong trào tết trồng cây, chi đoàn thanh niên dự định trồng 120 cây xanh. Khi bắt đầu thực hiện, chi đoàn được tăng cường thêm 3 đoàn viên. Gọi x là số đoàn viên ban đầu của chi đoàn và giải sử số cây mà mỗi đoàn viên trồng được là như nhau. Viết phân thức biểu thị theo x.

a) Số cây mỗi đoàn viên trồng theo dự định.

b) Số cây mỗi đoàn viên trồng theo thực tế.

c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế.

Phương pháp:

Số cây mỗi đoàn viên trồng được bằng tổng số cây chia cho tổng số đoàn viên.

Lời giải:

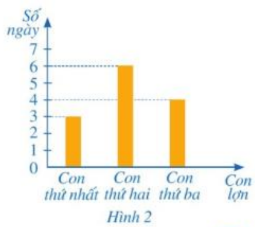
Bài 8 trang 43 SGK Toán 8 tập 1 - Cánh Diều

Gia đình cô Lương nuôi ba con lợn con. Cả ba con lợn đều ăn cùng một loại thức ăn gia súc. Biểu đồ cột ở Hình 2 biểu diễn số ngày mà mỗi con lợn ăn hết một bao thức ăn. Hỏi cả ba con lợn ăn trong x ngày \((x \in \mathbb{N}*)\) thì cần bao nhiêu bao thức ăn?

Phương pháp:

Qua biểu đồ phân tích và tính toán mỗi con lơn 1 ngày ăn hết bao nhiêu phần bao thức ăn.

Suy ra ba con lợn một ngày ăn hết bao nhiêu phần bao thức ăn.

Lời giải:

Sachbaitap.com