Giải SGK Toán 8 trang 47 Kết nối tri thức tập 1Giải bài 2.28, 2.29, 2.30, 2.31, 2.31, 2.33, 2.34, 2.35 trang 47 SGK Toán lớp 8 kết nối tri thức tập 1. Khẳng định nào sau đây là đúng? A. Trắc Nghiệm Bài 2.28 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Đa thức \({x^2} - 9x + 8\) được phân tích thành tích của hai đa thức A. \(x - 1\) và \(x + 8\) B. \(x - 1\) và \(x - 8\) C. \(x - 2\) và \(x - 4\) D. \(x - 2\) và \(x + 4\) Lời giải: \({x^2} - 9x + 8 = {x^2} - x - 8x + 8 = \left( {{x^2} - x} \right) - \left( {8x - 8} \right) = x\left( {x - 1} \right) - 8\left( {x - 1} \right) = \left( {x - 1} \right)\left( {x - 8} \right)\) Chọn B. Bài 2.29 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Khẳng định nào sau đây là đúng? A. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + 2AB + {B^2}\) B. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - 2AB + {B^2}\) C. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + {B^2}\) D. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - {B^2}\) Lời giải: \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) Chọn D. Bài 2.30 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Biểu thức \(25{x^2} + 20xy + 4{y^2}\) viết dưới dạng bình phương của một tổng là: A. \({\left[ {5x + \left( { - 2y} \right)} \right]^2}\) B. \({\left[ {2x + \left( { - 5y} \right)} \right]^2}\) C. \({\left( {2x + 5y} \right)^2}\) D. \({\left( {5x + 2y} \right)^2}\). Lời giải: \(25{x^2} + 20xy + 4{y^2} = {\left( {5x} \right)^2} + 2.5x.2y + {\left( {2y} \right)^2} = {\left( {5x + 2y} \right)^2}\) Chọn D. Bài 2.31 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Rút gọn biểu thức \(A = {\left( {2x + 1} \right)^3} - 6x\left( {2x + 1} \right)\) ta được A. \({x^3} + 8\) B. \({x^3} + 1\) C. \(8{x^3} + 1\) D. \(8{x^3} - 1\) Lời giải: \(\begin{array}{l}A = {\left( {2x + 1} \right)^3} - 6x\left( {2x + 1} \right) = {\left( {2x} \right)^3} + 3.{\left( {2x} \right)^2}.1 + 3.2x{.1^2} + {1^3} - \left( {6x.2x + 6x.1} \right)\\ = 8{x^3} + 12{x^2} + 6x + 1 - 12{x^2} - 6x = 8{x^3} + \left( {12{x^2} - 12{x^2}} \right) + \left( {6x - 6x} \right) + 1 = 8{x^3} + 1\end{array}\) Chọn C. B. Luyện Tập Bài 2.32 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Tính nhanh giá trị của các biểu thức: a) \({x^2} - 4x + 4\) tại x=102. b) \({x^3} + 3{x^2} + 3x + 1\) tại x=999. Lời giải: a) \({x^2} - 4x + 4 = {x^2} - 2.x.2 + {2^2} = {\left( {x - 2} \right)^2}\) Thay \(x = 102\) vào biểu thức ta được \({\left( {102 - 2} \right)^2} = {100^2} = 10000\) b) \({x^3} + 3{x^2} + 3x + 1 = {\left( {x + 1} \right)^3}\) Thay x=999 vào biểu thức ta được \({\left( {999 + 1} \right)^3} = {1000^3} = 1000000000\) Bài 2.33 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Rút gọn các biểu thức: a) \(\left( {2x - 5y} \right)\left( {2x + 5y} \right) + {\left( {2x + 5y} \right)^2}\) b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\) Lời giải: a) \(\begin{array}{l}\left( {2x - 5y} \right)\left( {2x + 5y} \right) + {\left( {2x + 5y} \right)^2}\\ = \left( {2x + 5y} \right)\left( {2x - 5y + 2x + 5y} \right)\\ = \left( {2x + 5y} \right).4x\\ = 2x.4x + 5y.4x\\ = 8{x^2} + 20xy\end{array}\) b) \(\begin{array}{l}\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\\ = {x^3} + {\left( {2y} \right)^3} + {\left( {2x} \right)^3} - {y^3}\\ = {x^3} + 8{y^3} + 8{x^3} - {y^3}\\ = \left( {{x^3} + 8{x^3}} \right) + \left( {8{y^3} - {y^3}} \right)\\ = 9{x^3} + 7{y^3}\end{array}\) Bài 2.34 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Phân tích các đa thức sau thành nhân tử: a) \(6{x^2} - 24{y^2}\) b) \(64{x^3} - 27{y^3}\) c) \({x^4} - 2{x^3} + {x^2}\) d) \({\left( {x - y} \right)^3} + 8{y^3}\) Lời giải: a) \(6{x^2} - 24{y^2} = 6.\left( {{x^2} - 4{y^2}} \right) = 6\left[ {{x^2} - {{\left( {2y} \right)}^2}} \right] = 6\left( {x - 2y} \right)\left( {x + 2y} \right)\) b) \(64{x^3} - 27{y^3} = {\left( {4x} \right)^3} - {\left( {3y} \right)^3} = \left( {4x - 3y} \right)\left[ {{{\left( {4x} \right)}^2} + 4x.3y + {{\left( {3y} \right)}^2}} \right] = \left( {4x - 3y} \right)\left( {16{x^2} + 12xy + 9{y^2}} \right)\) c) \({x^4} - 2{x^3} + {x^2} = {x^2}.\left( {{x^2} - 2x + 1} \right) = {x^2}.{\left( {x - 1} \right)^2}\) d) \(\begin{array}{l}{\left( {x - y} \right)^3} + 8{y^3} = {\left( {x - y} \right)^3} + {\left( {2y} \right)^3} = \left( {x - y + 2y} \right)\left[ {{{\left( {x - y} \right)}^2} - \left( {x - y} \right).2y + {{\left( {2y} \right)}^2}} \right]\\ = \left( {x + y} \right)\left( {{x^2} - 2xy + {y^2} - 2xy + 2{y^2} + 4{y^2}} \right)\\ = \left( {x + y} \right)\left( {{x^2} + 7{y^2}} \right)\end{array}\) Bài 2.35 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).
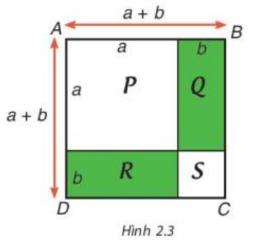
Lời giải: Diện tích hình vuông ABCD là: \({\left( {a + b} \right)^2}\) Diện tích hình vuông ABCD là: \({S_{ABCD}} = {S_P} + {S_Q} + {S_R} + {S_S} = {a^2} + ab + ab + {b^2} = {a^2} + 2ab + {b^2}\) Do đó \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\) Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 2
|

 Tải ngay
Tải ngay